Geometrische Beziehungen bei der Vermischung von Dimensionen
In vielen Prozessen der Natur und der Gesellschaft wird etwas ausgetauscht oder transportiert, sind also „Ströme“ festzustellen. Sobald diese Ströme nicht nur im Inneren von etwas fließen, sondern dieses eine „Etwas“ über eine Grenze verlassen und in ein anderes „Etwas“ gelangen, so haben wir es mit unterschiedlichen Dimensionszahlen zu tun, denn eine „Grenze“ hat immer eine Dimension weniger als das, was durch sie begrenzt wird.
Beispiele:
Die Grenze zwischen zwei Flächen (z.B. Stadtbezirke, also zweidimensional) ist eine Linie (eindimensional).
Die Teilung einer Strecke (eindimensional) in zwei Teile benötigt einen teilenden Punkt (nulldimensional).
Zwei Volumina (dreidimensionale Konvektionszellen) werden durch eine Trennfläche (zweidimensionale Zellwand) geteilt.
Bei vielen Prozessen spielen die Grenzen genauso eine Rolle wie die beiden „Etwas“, das durch sie getrennt wird. In welchem Verhältnis diese beiden Rollen stehen, ist jedesmal anders. Da aber bei ähnlicher Vergrößerung des Ganzen die unterschiedlichen Dimensionen von „Etwas“ und „Grenze“ unterschiedlich wachsen, muss es notwendigerweise absolute Größen geben, bei denen das Verhältnis zwischen beiden ausgewogen ist.
Weit entfernt von dieser Ausgewogenheit hat man dann Veranlassung, bei einer groben Betrachtung des Problems auf den wesentlich kleineren Anteil „begründet vernachlässigend“ zu verzichten.
Da man das Ganze auch abstrakt auf die Zahl unabhängiger Variabler erweitern kann, sollte man das Problem auch für größere Dimensionszahlen angehen.
Frage: Kann man einfache praktische Beispiele vorweg schicken?
Antwort: Klar doch! Wieso sind am Strand alle Sandkörner gleich groß? Wieso sind alle Sandriffel gleich hoch und gleich weit entfernt? Wieso braucht die Mücke kein Herz und wieso trinkt sie ohne Zungen-Muskel-Vakuum unser Blut? Warum gibt es in der Natur Mineralien, die einen so hohen Druck zu ihrer Entstehung brauchen, dass die Temperatur der zum Druck gehörenden Tiefe sie schmelzen lassen müsste und sie also gar nicht existieren dürften?
Wir sind also mitten beim Haupt-Thema dieser Website: Strukturen bewundern und verstehen und noch mehr bewundern!
Fangen wir also klein an:
1. Gleichheit von Rand und Innen im eindimensionalen Fall
Sofort erkennen wir ein grundlegendes Problem: Wie vergleicht man Äppel mit Birnen (unterschiedliche Dimensionszahlen!)?
Wir entnehmen der Praxis-Erfahrung, dass nur in der Theorie der Rand undendlich dünn ist, in der Praxis aber eine endliche Dicke hat und somit „eigentlich“ die gleiche Dimensionszahl besitzt wie das, was er begrenzt.
Am einfachsten versinnbildlicht man sich das, wenn man kongruente Elemente der Innen-Dimensionalität heranzieht, um das Prinzip darzustellen. Dann wäre also eine Strecke zu betrachten, die in gleichlange Teilstrecken zerlegt wird, von denen natürlich zwei an den beiden Enden der Strecke liegen (es sind die beiden „Ränder“) und der Rest im „Inneren“.
Die Lösung ist nun ganz einfach: Wenn das Innere die gleiche Länge (Anzahl der Elemente) haben soll wie die Grenze, so folgt aus Grenze = 2, dass auch das Innere = 2 sein muss.
Haben die Elemente beider Typen (Rand und Inneres) eine gleichgroße Wirkung auf eine bestimmte zu untersuchende Gesamteigenschaft, so ist genau diese Zahl 4 der Übergang zwischen der Dominanz der einen oder anderen. Sind ihre Einflüsse verschieden und in ihrem Unterschied bekannt, so kann mit dem zwischen ihnen bestehenden Verhältnis multiplizert werden und der indifferente Fall ist gefunden.
Spannender ist der umgekehrte Fall, wo man durch Variation der Länge den Fall der Indifferenz sucht und im Umkehrschluss auf die Beiträge der beiden Typen schließt.
Gibt es das auch in der Praxis? Na klar! Ein einfach zu verstehendes Beispiel sollte ein Hindernislauf sein, ein etwas technischeres die Wärmeleitung.
Hindernislauf: Es ist ein Wassergraben zu überwinden, ein Brennesselfeld zu durchqueren und wieder ein Wassergraben zu überwinden. Wer gewinnt? Der Weitspringer oder der Dickhäutige? Es kommt offenbar auf die Qualitäten des Grabens, der Brennesseln, des Springers und der Schienbeinhaut an. Es gibt mit Sicherheit einen Satz an Parametern, wo beide gleich schnell sind. Nach Ähnlichkeitsgesetzen kann dieser Satz sogar in andere Sätze transformiert werden
Wärmeleitung: Die Wärmeenergie der Zimmerluft muss einen Übergang zur Wand, einen Durchgang durch die Wand und einen Übergang zur Außenluft überwinden, bevor sie vom Winde verweht wird. Diese Reihenschaltung kann je nach Wanddicke vom einen oder anderen Parameter dominiert werden, dazwischen gibt es Gleichheit. (Siehe analoges geologisches Beispiel ganz unten, dort aber um den Parameter Zeit erweitert!)
2. Gleichheit von Rand und Innen im zweidimensionalen Fall
Jetzt ist es schon nicht mehr so einfach, selbst dann nicht, wenn wir Gleichheit in der Wirkung von Rand und Innen voraussetzen und alles mit Quadraten darstellen wollen. Welches Rechteck erfüllt die Bedingung, dass es genausoviele Rand-Quadrate wie Innen-Quadrate (oder kongruente Rand- und Innen-Rechtecke gleicher Orientierung!) besitzt?
Mit der Erfahrung des eindimensionalen Falles kann man sich ein Rechteck aus Streifen zusammengesetzt denken und annehmen, diese Streifen wären alle 4 Quadrate lang. Gut, das geht beinahe auf, wenn da nicht die andere beiden Ränder wären. Bei einem Quadrat aus 4 solcher 4-er-Streifen hätten wir eben nicht 8 Innen- und 8 Außen-Quadrate, sondern nur 4 Innen und 12 Außenquadrate, weil das Rechteck, egal, wie lang wir es machen, immer zwei Endstreifen haben wird, die 4 statt nur 2 Außen besitzen, eben weil es ja die Randstreifen sind. Mit jedem Zusatzstreifen zu dem 4 x 4 -Rechteck kommen 2 Innen und 2 Außen dazu, was im Unendlichen den Unterschied des Anfangs (4 gegen 12) verschwinden lässt (z.B. bei 1000 zusätzlichen Streifen (2004 gegen 2012, was fast gleichgroß ist).
Aber Geometrie soll ja eine Übung des exakten Denkens sein, weshalb wir also nach einer exakten Lösung suchen.
Der logische Gang wäre jetzt so:
Da der Rand bei 4-er-Streifen zu groß ist, verlängern wir auf 5-er-Streifen und suchen die richtige Länge des 5 x n – Rechtecks.
Wir erkennen ein Muster: Mit jedem neuen Streifen kommen 2 Rand- und 3 Innen-Elemente hinzu. Das Innen holt also pro Streifen um 1 auf!
Beginnt man mit 5 x 5 (9 Innen und 16 Rand), braucht man also 16-9=7 Zusatzstreifen für die Gleichheit: 12 x 5 sollte also die Lösung sein. Probe: Innen 10*3 =30, Gesamt 12*5=60, also Halbe-Halbe! Genaue Probe: 2 Ränder mit 12 sind 24, 2 Ränder mit 5-2=3 sind 6, 24+6=30. In Ordnung!
Aber: Ist das die einzige Lösung? könnte man auch mit einem anderen Quadrat beginnen?
Gesamt 6*6=36, Innen 4*4=16, Rand muss also 20 sein (Probe: 2*6+2*4=20, erfüllt).
Mit jedem neuen Streifen kommen 2 Rand und 4 Innen hinzu. (20-16)/2 = 2, wir brauchen also 2 Zusatzstreifen:
6 x 8 – Rechteck sollte die zweite Lösung sein.
Probe: Alles: 6*8=48; Innen: 4*6=24, also Außen 48-24=24. Stimmt. Probe der Probe: 2*8+2*(6-2)=24.
Das nächstgrößere Quadrat is 7 x 7 =49 (25 Innen + 24 Rand). Es ist nicht mehr zu korrigieren, genausowenig wir die noch größeren, denn der Innenanteil hat nun die Oberhand.
Für die Theoretiker hier die Frage, ob man das auch analytisch lösen könnte?
Versuchen wir es:
Rand : 2*L + 2*(B-2) = 2*L + 2*B – 4
Innen: (L-2)*(B-2) = L*B – 2*L – 2*B + 4
Alles: L*B
In der Gleichung taucht eine interessante Größe auf, nämlich „der Rand des Randes“, die Zahl der Ecken! Die eindimensionalen Ränder überschneiden sich in den nulldimensionalen Eckpunkten, die im Quadrat-Element-Modell des Rechtecks natürlich 4 einzelne Quadrate sind.
Setzt man die beiden Ausdrücke für Rand und Innen gleich, erhält man die Gleichung
L*B = 4*L + 4*B – 8 = 4*(L+B) – 8
(Neben-Bemerkung: Die Form der Gleichung darf uns gar nicht verwundern, denn durch die Gleichberechtigung von Länge und Breite können nur Kombinationen der beiden Größen als Produkt oder Summe vorkommen, denn für diese gilt das Kommutativ-Gesetz. Grafisch wären das also alle Kurven, die sich an L=B gespiegelt selber decken, hier also parallele Geraden (-45°) und Hyperbeln!)
Für welche ganzzahligen L und B ist die Gleichung erfüllt? (Zusatzbedingung „ganzzahlig“ führt zur „Diophantischen Gleichung“, welche mehrere diskrete Lösungen für mehrere Variablen besitzen kann.)
Versuch 1:
Wir formen die Gleichung zu einer Funktion um:
L*B – 4*L = 4*B – 8
L = 4 * (B-2)/(B-4)
Wenn L ganzzahlig sein soll, darf B nicht zu groß sein, denn für große B geht der Bruch auf der rechten Seite „von unten“ gegen 1, mit 4 multipliziert also gegen 4, ohne ganzzahlig zu werden.
Chancen gibt es also nur, wenn der Bruch Viertel, Halbe oder Ganze darstellt. Damit er positiv ist, muss B>4 sein. Also probieren:
B=5 -> Bruch=3/1 -> L=12 OK
B=6 -> Bruch=4/2 -> L=8 OK
B=7 -> Bruch=5/3 -> L=20/3
B=8 -> Bruch=6/4 -> L=6 OK
B=9 -> Bruch=7/5 -> L=28/5
B=10 -> Bruch=8/6 -> L=32/6
B=11 -> Bruch=9/7 -> L=36/7
B=12 -> Bruch=10/8=5/4 -> L=5 OK
Hier darf man abbrechen, denn die weitere Folge würde für L zu kleineren Werten als 5 führen müssen, was wegen der Symmetrie der Aufgabenstellung genausowenig erlaubt ist wie B<5 (B>4 war die Bedingung oben!). (Streng genommen hätte man schon bei B=8 aufhören dürfen!)
Es haben sich (eingedenk der Vertauschbarkeit) nur 2 verschiedene Pärchen ermitteln lassen, nämlich (5; 12) und (6; 8).
Versuch 2:
Mit dem „Trick“ einer Koordinaten-Transformation um 4 (eindimensionale Lösung als Grenzfall!) erhält man eine einfachere Gleichung, wenn l=L-4 und b=B-4 sein soll, L also durch l+4 und B durch b+4 ersetzt wird:
(l+4)(b+4) = 4(l+4) + 4(b+4) – 8
l*b +4l + 4b + 16 = 4l + 16 + 4b +16 – 8
l*b = 8
Hier gibt es nur 2 ganzzahlige Paare, wenn man Vertauschungen außer Acht lässt:
1*8 und 2*4
Die Rück-Transformation mit L=l+4 und B=b+4 ergibt die „echten“ Rechteckseiten zu:
5*12 und 6*8
Weitere kann es nicht geben, wenn man die um 90° gedrehten Rechtecke (Vertauschung von Länge und Breite) nicht als „Neue“ bewertet.
Die grafische Darstellung dieser Lösungen wären solche Punkte einer Hyperbel l*b=8 (oder als Funktion dargestellt l=8/b), welche auf einem Kreuzungspunkt ganzzahliger Hilfslinien der beiden Koordinaten liegen.
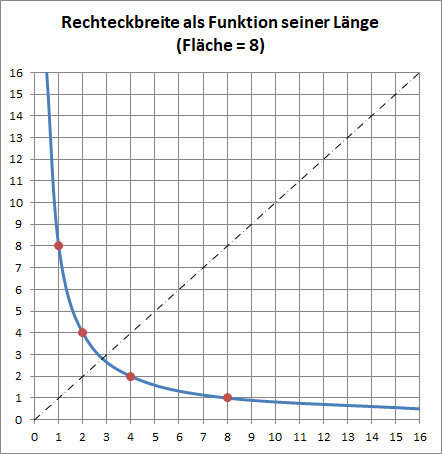
Die Kurve geht dicht an 3 x 3 (also 7 x 7!) vorbei, weitere Schnitte kann es offenbar wirklich nicht geben.
3. Gleichheit von Rand und Innen im dreidimensionalen Fall
Der Probier-Ansatz (der „empirische“) würde nun so lauten, ein „funktionierendes“ Rechteck zu stapeln, dann korrigieren (wegen der Endflächen!!) zu müssen und dann die Höhe des Quaders zu ermitteln.
Wir nehmen als0 gleich 5*13 statt 5*12, weil wir ja wissen, dass es sonst wegen der Endflächen im Endlichen nicht „gehen“ kann!
Jede Endfläche hat 5*13=65 Würfelchen (das ist jetzt die Einheit!), es müssen also 130 Einheiten ausgeglichen werden, wenn wir mit 5*13*2 beginnen.
Mit jeder Schicht gibt es einen Innen-Überschuss von
3*11 – (2*13+2*(5-2)) = 33 – 32 = 1 Würfel.
Nach 130 Zusatz-Schichten sollten wir also am Ziel sein:
5 x 13 x 132 ist eine Lösung (Probe selber machen!)
Probieren wir es auch mit der anderen Lösung des zweidimensioalen Falles, dem Rechteck 6 x 8:
Wir erhöhen auf 7 x 8 und kommen zu folgenden Zahlen:
Jede Endfläche hat 56 Elemente, wir müssen als 112 ausgleichen.
Das Rechteck 7 x 8 hat 5*6=30 Innen und 2*7+2*6=26 Außen, wir machen also pro Schicht 4 gut.
112/4=28, insgesamt also mit den beiden Randschichten 30 Schichten.
Das wäre ein Quader mit den Maßen 7 x 8 x 30. Der hat genau
L*B*H = 5*6*28 = 840 Innenwürfel und
2*L*B + 2*L*H + 2*B*H – 4L – 4B – 4H + 8 = 840 Außenwürfel.
(Von den 6 Flächen müssen die doppelt gezälten 12 Kanten abgezogen werden und die dann dreifach verschwundenen dreifach gezählten Ecken wieder ergänzt werden.)
Auch mit der Erhöhung von 6 x 8 auf 6 x 9 klappt es mit dem Ergebnis als Quader 6 x 9 x 56.
Hier müssen 2*6*9=108 Würfelchen durch 54 Schichten mit je 2 Überschuss (4*7=28 gegen 2*9+2*4=26) ausgeglichen werden.
Kann man hier auch analytisch vorgehen, um zu prüfen, ob es weitere Lösungen gibt?
Man kann immer aus der Gleichsetzung von Innen und Rand (manchmal auch „Außen“ genannt, was aber eventuell missverständlich ist) eine Gleichung machen, die als Bestimmungsgleichung umgeformt ist.
Im Dreidimensionalen wäre das so (selber transformieren mit 4 und nachrechnen!):
h = 8*(b+l+6)/(b*l – 8)
Trägt man das als Höhe über dem ersten Quadranten eines zweidimensionalen Koordinatensystems ab (nur positive Längen zugelassen), so erhält man wieder ausgewählte Punkte (19 unterschiedliche Lösungen, die nicht durch Vertauschung entstehen), die auf den Kreuzungspunkten der ganzzahligen Hilfsflächen der drei Koordinatenpaare liegen müssen und die man in einer EXCEL-Tabelle mit einer WENN-Funktion (für die Ganzzahligkeit der Höhe) separieren und dann farblich hervorheben kann:

Diese Kreuz-Tabelle ist so zu lesen: Der von Null verschiedene Tabellenwert ist die Höhe des Quaders, die beiden äußeren Zahlen in Spalten und Zeilen sind Breite und Länge. Dunkelrot ist der würfelähnlichste Quader (8 x 10 x 12) mit dem kleinsten Volumen dargestellt, grün der längste (5 x 13 x 132) mit dem größten Volumen. Auch hier liegen vier „verwandte“ Lösungs-Gruppen auf Hyperbeln als parallele ebene Schnitte eines Hyperboloids (H=6; 7; 8; 9; 10)!
Nur zwei Quader haben einen quadratischen Querschnitt, liegen auf der Diagonalen der Kreuztabelle:
(8*8*18) und (7*7*100).
Aus „kristallografischer“ Sicht ist interessant, dass auch so ein langprismatisches Teil wir der quadratische (7*7*100) und erst recht der etwas abgeflachte (5*13*132) unter gewissen Umständen als „Übergangs“-Formen zwischen OF- und V-Dominanz ist: Einmal als „Whisker“ und einmal als flache Zunge. Die (24*22*5) geht dann schon in die Plättchen-Form über.
Diese Aufgabe lässt sich auch interessant variieren:
Was wäre, wenn wir den Quader auf einer Unterlage aufsitzen ließen und die dort befindlichen Bausteine NICHT zur Oberfläche zählten? Ist das mit der Frage nach dem halben obigen Quader zu beantworten? Wir werden sehen. Jedenfalls sind die Dimensionen nun neu gemischt. (Eines darf man voraussagen: halbe ungerade Längen sind nicht ganzzahlig und scheiden schon einmal aus, weshalb die mögliche Vielfalt abnehmen sollte, dafür kommen aber flachere Objekte hinzu…)
Die Bedingung heißt also:
Innenraum = 5 Flächen – 8 Kanten +4 Ecken
(a-2)(b-2)(c-1) = (ab+2ac+2bc)–(2a+2b+4c)+4
Umgestellt ergibt das im unsymmetrischen Fall (Berechnung einer aufliegenden Kante, hier a):
a = (4bc-4b-8c+8)/(bc-2b-4c+4)
und im symmetrischen Fall (Berechnung einer freien Kante, also der senkrechten c):
c = (2ab-4a-4b+8)/(ab-4a-4b+8)
Beide sollten füreinander als Probe dienen können.
Hier die Kreuztabellen:

Gültige aufliegende Quader für „innen gleich außen“ im unsymmetrischen Ansatz, Höhe als ganz linke Bezugsspalte
Und wirklich: Der zum Beispiel gültige 15 Einheiten hohe Quader mit der Basisfläche (8 x 7) ist bei der unsymmetrischen Tabelle ebenso enthalten wie auch in der der freien Quader, dort aber mit (30 x 8 x 7) Einheiten, also der doppelten Höhe.
Nun gibt es selbstredend noch flachere „Plättchen“ als bei den freien Quadern, z.B. die Formen (3 x 14 x 16) als fast quadratisch oder (3 x 10 x 32) als längliche Zunge. Die längsten gefundenen und fast quadratischen Whisker sind aufliegende mit den Maßen (7 x 5 x 72) und (3 x 9 x 56) und stehende mit den Maßen (50 x 7 x 7) (der halbe Whisker (100 x 7 x 7) von den oben beschriebenen freien!) und (66 x 13 x 5), wobei die erste Zahl jeweils die freie Höhe ist.
Wozu das Ganze nütze ist? Es ist eine Übung für den Umgang mit unterschiedlichen Dimensionen, wie sie immer bei „Selbstorganisation“ zu Strukturen führen. Hier ist noch eine Diversifizierung der Randbedingungen hinzugekommen.
4. Gleichheit von Rand und Innen im vierdimensionalen Fall
Man kann das Spiel sogar noch weiter treiben und dann 392 4-dimensionale Quader ermitteln, die diese Bedingung der Gleichwertigkeit von einlagigem dreidimensionalem Rand und vierdimensionalem Innenvolumen erfüllen.
Auch hier müssen wieder Mehrfachzählungen durch Überschneidung ausgeglichen werden, was sich aber wieder automatisch durch Ausmultiplizieren der Formel für das Innen ergibt:
Vi = (a-2)(b-2)(c-2)(d-2) = abcd – 2(abc+abd+acd+bcd) + 4(ab+ac+ad+bc+bd+cd) – 8(a+b+c+d) + 16
Die umgestellte Bestimmungsgleichung ist dann:
a = 2*(2bcd-4(bc+bd+cd)+8(b+c+d)-16)/(bcd-4(bc+bd+cd)+8(b+c+d)-16)
Das lässt sich dann mit einer entsprechend pfiffig aufgebauten Mehrfach-Schleife in erträglichen Zeiten abfragen und tabellieren.
Der würfelähnlichste Quader ist auch der Kleinste:
11 * 12 * 13 * 15 mit einem Volumen von 25.740
Der „längste“ der 392 hat wieder das größte Volumen:
5 * 13 * 133 * 17.292 mit dem Volumen von 149.489.340
Dazwischen gibt es schöne Sonderfälle mit zwei gleichen Abmessungen („quadratisch“) wie z.B.:
10 * 12 * 12 * 20 mit einem Volumen von 28.800.
Für alle, die schon wieder ächzen und schon wieder nach ANWENDUNG rufen, hier zwei einfache Beispiele aus der Geologie (auch in der Kristallografie könnte man Beispiel anführen, aber die findet man ja dort in den entsprechenden weiterführenden Seiten sowieso, wenn Wachstum an Flächen, Kanten und Ecken unterschiedlich verläuft und zum Beispiel zu Skelett-Kristallen, Dendriten, Whiskern oder gar Kugelkristallen statt zu den isometrischen Idealkörpern als Vergrößerung der Elementarzelle führt):
Beispiel 1: Erwärmung oder Abkühlung von Kontinentalplatten beim Eintauchen oder Auftauchen
Wie lange dauert es eigentlich, bis dicke Platten erwärmt oder abgekühlt sind?
Eine realitätsnahe Rechnung müsste auch die Plattenbewegung selbst berücksichtigen. Nimmt man an, dass die Platten plötzlich verschoben werden, bekommt man natürlich andere Werte. In welcher Richtung sind die Werte anders? Das kommt darauf an, wohin man den Zeit-Nullpunkt legt: Legt man ihn an den Anfang des Eintauchens so ist der „wahre“ Ablauf länger, legt man ihn ans Ende, kürzer.
Wie lange dauert das Eintauchen?
Wenn man davon ausgeht, dass „normale“ Driftgeschwindigkeiten der Kontinente bei 2cm/a liegen (Drift-Rekord: Indien nach Norden mit 20cm/a vor der Kollision mit Asien, heute noch 5cm/a!), so werden in 1Ma (1 Million Jahre) 20 km zurückgelegt. Man kann also bei einem vertikalen Temperaturgradienten von 30K/km in der Erdkruste davon ausgehen, dass es mindestens 2Ma dauert (etwas schräg eingetaucht!), bis etwa eine Tiefe von 30 km und damit etwa 1000°C erreicht sind. Vergleicht man das mit dem Prozess der Durchwärmung (hier ohne Phasenübergänge von Gesteins-Bestandteilen gerechnet), so kommt man auf ähnliche Werte:
Temperatur-Verlauf nach 10Ma (je 20 Kurven nach je 500.000 Jahren) für Kontinentalplattendicken von 5, 10, 21 und 35 km (20°C „plötzlich“ in 1000°C getaucht) (rechts und links sind modellhaft etwa gleichdicke Bereiche festen Gesteins angenommen und danach durch Konvektion bei 1000°C fixiert). Die etwa vierfache Dicke (z.B. 21 gegen 5 km) führt auch hier zu einer knapp zwanzigfachen Zeit, also quadratisch abhängig, wie unten auch im Beispiel 2 zu sehen.
Die Ähnlichkeit der Zeitspannen für Eintauchen und Aufwärmen ist von wesentlicher Bedeutung für das Verständnis, warum man (z.B. im Erzgebirge) Mineralkristalle (z.B. Zirkone) findet, die unter solchen Drücken entstanden sein müssen, unter denen „normalerweise“ bei statischem Aufbau der Erdkruste Temperaturen herrschen müssten, die den Kristall unmöglich machen: Eine abgetauchte Platte geriet unter hohen Druck, ohne komplett durchgewärmt worden zu sein, bevor sie durch die Auftriebskräfte (sie hat eine geringere spezifische Dichte als die Flüssigkeit, in die sie geschoben wird!!) längs zerriss und wieder auftauchte („exhumiert“ worden ist, wie die Tektoniker sagen).
Beispiel 2: Verwitterung von Felsen durch Temperaturwechsel
Nehmen wir Felsgestein, das der Witterung ausgesetzt ist. Wie tief dringen die Temperaturschwankungen des Tages oder des Jahres ein und welchen Anteil am Gesamtfelsen macht das aus? Man merkt schon, dass die Form des Felsens eine Rolle spielt, denn für eine Ebene ist die Lösung relativ einfach. Die denktechnologische Frage ist es dann, wie man den „ebenen Fall“ zum „konkreten Felsen“ wandeln kann.
Neben-Bemerkung: Wieso gehen wir davon aus, dass die Schwankungen nicht unendlich tief eindringen, so wie Wellen zum Beispiel? Na ganz einfach: Wenn es draußen nach der Hitze kalt wird, liegt die Temperatur unter dem Mittelwert, und vom aufgewärmten Inneren fließt der größere Teil wieder nach außen und der kleinere Teil weiter nach innen, wo sich der Mittelwert eingestellt hat. Dann polt sich alles um und hebt sich also („aus Symmetriegründen“) auf. Aber es gibt doch Wellen? Klar. Dann gibt es entweder eine Trägheit (also Masse und somit kinetische Energie) oder einen Energie-Austausch wie zwischen magnetischem und elektrischem Feld. Wir erwarten also eine „evaneszente Temperatur-Welle“, eine nach innen schnell verschwindende Temperaturschwankung.
Das ist also ein Problem der Wärmeleitung, verknüpft mit den Kapazitäten für Wärmeenergie. Der „Wärme-Energie-Füllungs-Zustand des Speichers“ wird durch seine „Temperatur“ charakterisiert. Dabei treten folgende zwei Proportionalitäten gleichzeitig auf (Erstes und zweites Fick‘sches Gesetz):
– Je größer das Temperaturgefälle (Temperatur-Differenz bezogen auf einen Abstand, z.B. auf eine diskrete Schichtdicke bei der numerischen Integration), desto größer die Wärmestromdichte
– Je größer die Wärmekapazität einer Schicht (deren Volumen ist Fläche mal Schichtdicke), desto geringer die Temperaturänderung in einem Zeittakt bei gegebenem Wärmestrom (Wärmestromdichte (Bilanz aus Zustrom und Abstrom!) mal Fläche)
Daraus ergibt sich folgende Vorschrift für die numerische Zeit-Integration der Temperatur einer Tiefenschicht (der Felsen wird also in „finite Elemente“ zerlegt, sinnvollerweise hier also parallel zur Oberfläche liegende Schichten), wobei die Integration erst für alle Schichten erfolgen muss, bevor der nächste Zeittakt beginnt (Berechnung aller neuen Werte jeweils aus allen alten, damit keine Quer-Beeinflussung innerhalb eines Zeit-Taktes entsteht!!):
ΔTemp = (Templi + Tempre – 2*Temp)/Dicke*spWärmeleitf/(spWärmekap*Dicke*Dichte) * Δt
Die diskrete erste Klammer steht sozusagen für die zweite Orts-Ableitung der Temperatur aus der Diffusions-Differentialgleichung
dT/dt = λ/(ρ*cw)*d²T/dx² (λ spWärmeleitf, ρ Dichte, cw spWärmekap)
Man kann somit schon a priori schließen, dass folgende zwei Erwartungen erfüllt sein müssten
-E1: dass die erforderliche Zeit für eine bestimmte Temperaturänderung einer Schicht (bei gegebener Temperaturdifferenz) quadratisch mit ihrer Dicke steigt (Temperaturgefälle sinkt UND Wärmekapazität steigt)
-E2: dass die Eindringtiefe einer periodischen Außentemperaturschwankung wenig mit deren Amplitude zusammenhängt
Dazu kann man eine Modellrechnung mit einer harmonisch schwingenden Außentemperatur gestalten, wobei man deren Amplitude und Frequenz als Parameter frei hält wie auch die Dichte und Wärmekapazität sowie Wärmeleitfähigkeit des Materials. Zusätzlich braucht man noch die Wärmeübergangszahl zwischen beiden Medien und am besten eine Konvektion im äußeren Medium, damit es keine Rückwirkung dorthin gibt. Das ergibt dann eine Diskretisierung von Ort (eindimensional, nur Tiefe!) und Zeit in hier z.B. 2,5 Mio EXCEL-Zellen (auf meinem Rechner dauert eine Formeländerung in der Tabelle etwa 30 min, eine Berechnung 5 Sekunden, man sollte also besser eine gute Programmiersprache verwenden: 250 * 10.000 Zellen Ort*Zeit).
Welche Erwartungen gehen nun in Erfüllung?
a) Einfluss der Temperatur-Amplitude
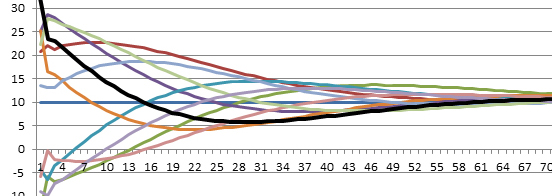

Man erkennt, dass eine Verdoppelung (bzw. Halbierung) der Amplitude bei sonst gleichen Parametern keine erkennbare Veränderung der Eindringtiefe bringt. (Die uneterschiedlichen Farben deuten hier unterschiedliche Zeitpunkte an, die schwarze Kurve ist die letzte.) Der Jahres-Schwankung ist auch eine tägliche Schwankung überlagert worden (die Zacken ganz links im Diagramm!), deren relative Eindringtiefe also der Wurzel aus 1/365, was etwa 19 ist, entsprechen sollte, was offenbar wirklich so ist.
b) Einfluss der Schwingzeit


Man erkennt, dass die vierfache Schwingzeit (unten) etwa zur doppelten Eindringtiefe führt, wie das schon im vorigen Beispiel herausgearbeitet worden ist.
c) Einfluss der Materialeigenschaften
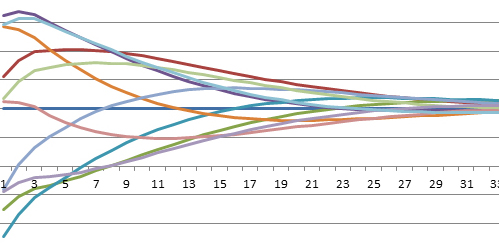

Man erkennt, dass eine höhere Wärmeleitfähigkeit (oben) zu einer höheren Eindringtiefe führt (z.B. wegen unterschiedlicher Gesteine). Das umgekehrte ist bei der Wärmekapazität der Fall.
Das Problem der Eindringteife von Temperaturschankungen betrifft zum Beispiel den Dauerfrost in den hohen Alpen-Lagen oder in der Tundra und die Wahrscheinlichkeit des Auftauens im Jahresrhythmus mit der Folge von Bergstürzen oder Gebäude-Schäden.
Zum anderen erklärt es die physikalische Verwitterung, indem man Zusatzfaktoren wie die sukzessive Zerklüftung durch Frostsprengung (verstärkend) und den sukzessiven Abtrag durch Abrutschen (abschwächend) je nach Hangneigung hinzufügen kann.
Nun kann man noch weiter spielen und eine leichte Konvektion (von zum Beispiel Wasser) überlagern, um den „summarischen phänomenologischen Wärmeleitkoeffizienten“ unsymmetrisch zu gestalten (z.B. nach innen stärker als nach außen). Dann geht das fast an den aperiodischen Grenzfall erinnernde Temperatur-Tiefen-Profil in eine leichte Schwingung über (hier 50% erhöht nach innen).
d) Einfluss einer aufgeprägten Richtungs-Unsymmetrie (z. B. durch strömendes Porenwasser!)




Oben der symmetrische Fall, dann zusätzlicher Transport nach innen, nach außen und Halbierung des Innentransports. Man erkennt: Jetzt können sich tatsächlich mehrere Wellenbäuche ausbilden, wenn der Transport nach innen geht!
(Der willkürlich gewählte Beginn mit der positiven Halbwelle der Temperatur setzt sich nach innen fort. Schaltet man das um, sind die negativen Werte optisch bevorzugt. Man sollte sich davon nicht täuschen lassen, dass auch der Beginn des Prozesses aus Test-Gründen mit angezeigt wird, was in der „richtigen“ Natur natürlich eigentlich nicht vorkommt, bei Bauwerken aber schon!)
Wichtigstes Fazit im Beispiel 2:
Der Zusammenhang zwischen Amplitude und Eindringtiefe ist tatsächlich fast verschwindend.
Wichtigstes Fazit beider Beispiele:
In jedem Fall kann (parameterabhängig!) eine bestimmte Dicke einer Grenzschicht ermittelt werden, welche für den Gesamtprozess zwischen Grenz-Dominanz und Innen-Dominanz einen Umschlagspunkt (der seinerseits wieder von der Gesamt-Geometrie abhängt) darstellt.
Beispiel n, n+1, …
Die Übertragung auf Alltagserscheinungen fällt nicht schwer:
- Ein Kleinkind friert schneller als ein Erwachsener, ein dünner erwachsener schneller als ein dicker, usw. usf.: Pro Kilogramm Körpermasse haben sie unterschiedlich viel Oberfläche, die im Winter Wärmeenergie abgeben kann. Die „Dimensionsrelation“ (Oberfläche pro Volumen) ist natürlich dimensionsbehaftet: 1/m. Im Body-Mass-Index ist das ebenso: Körpergewicht durch Quadrat der Körperlänge (kg/m²). Hier ist die Oberfläche nicht wirklich enthalten, sondern eher so etwas wie ein „Schlankheitsgrad“ berechnet worden.
- Ein Elefant benötigt dickere Beine als eine Mücke, und das nicht nur absolut, sondern auch relativ. Selbst wenn beider Beine aus demselben Material bestünden, müsste das so sein, denn das Gewicht wächst mit der dritten Potenz der Größe (Volumen-proportional), die Tragfähigkeit der Beine aber nur mit der zweiten (Querschnitts-proportional). Irgendwann wäre ein noch größeres Tier nur auf Beinen vorstellbar, deren Querschnitt größer als der Körperquerschnitt sein müsste, was einfach unsinnig ist. (Diese leben deshalb im Wasser, dessen Dichte sie selber auch haben, zur Not mit Hilfe von Schwimmblasen.)
- Ein kleines Tier fällt im Luftwiderstand langsamer als ein großes und hat ein relativ festeres Innen- oder Außenskelett als ein großes. Deshalb passiert ihm beim Absturz oder beim Flug gegen ein Fenster oder beim Zusammenstoß mit einem Regentropfen auch viel weniger.
- Beim Scaling-up oder Scaling-down in der Technik müssen diese Dimensionsrelationen auch beachtet werden, sonst passiert der größte Mist.
- Flutwellen in Flüssen, Bächen und Kanälen spiegeln die Dimensionsrelation von Wasserstand, Querschnitt und Durchfluss vermittels der Geschwindigkeit und der Reibung wider: Der hohe Wasserstand „überholt“ den niedrigen.
Dem kann jeder noch viel hinzufügen. Die Beispiele sensibilisieren dafür, wie sehr vieles in unserer Umgebung vom Maßstab abhängig ist.
Übrigens:
Wenn jemand sagt, so etwas finde man auch auf anderen Websites, so hat er völlig recht; aber den Spaß, es selbst gerechnet zu haben und dann mit den Parametern am eigenen Spielzeug forschen zu können, den findet man nirgends! (Selber essen mach fett…) Also: Nicht nur das hier durchlesen, sondern anstecken lassen und selber Ähnliches in Angriff nehmen!!!
Sollte man also „Physikalische Geometrie“ als neues Fach kreieren?







Kommentar abgeben