Grafische Darstellung
Warum nimmt man Diagramme als grafische Darstellung von Zusammenhängen?
Nun, man könnte denselben Zusammenhang auch als Tabelle darstellen oder einfach als Formel. Da aber das menschliche Auge im Zusammenhang mit dem Hirn und dem Gedächtnis hervorragend arbeitet, geben Diagramme (oder besser: Funktions-Graphen) einen schnellen Überblick über den Charakter eines Zusammenhangs.
Wie immer aber gibt es bei jedem „Werkzeug“ oder jeder „Abkürzung“ auch Tücken, derer man sich bewusst sein sollte.
Die Haupttücke eines „normalen“ Diagramms liegt darin, dass ein Vergleich der einfachsten Funktionen, nämlich der linearen, im allgemeinen über zwei Parameter erfolgt:
– Nulldurchgang oder „offset“
– Anstieg (Steigung) oder „slope“
Der Nulldurchgang bietet kein Problem, aber der Anstieg. Dieser ist nämlich das Verhältnis von Abszissen-Differenz und Ordinatendifferenz, bezogen auf zwei Wertepaare, also auf zwei Punkte der Funktion (hier: der Geraden). Dieses Verhältnis ist NICHT mit dem Winkel der Geraden zur Abszisse gleichzusetzen, sondern mit dem Tangens dieses Winkels. Die Tangens-Funktion hat nur in der Umgebung von -30° bis +30° ein etwa lineares Verhalten, dann saust sie davon. Das heißt, bei steilen Funktionsgraphen können wir uns in der Einschätzung des mathematischen „Anstiegs“ sehr stark verschätzen, denn eine Verdoppelung des mathematischen Anstiegs bewirkt NICHT mehr eine Verdoppelung des geometrischen Winkels der Geraden, denn dieser kann 90° schließlich nicht übersteigen!
Was hilft dagegen?
„Schlaue“ Programme wie die Tabellenkalkulation in EXCEL zum Beispiel stellen deshalb standardmäßig automatisierte Skalierungen zur Verfügung, damit der Winkel der linearen Funktion immer etwa im Verhältnis der geometrischen Abmessungen des Diagramms steht, also seiner Diagonalen folgt.
Das ist zwar „schlau“, aber auch „kontraproduktiv“, denn es beraubt das Diagramm seines Vorzugs, mit einem Blick Auskunft geben zu können, weil man nun erst die verwendeten Achsabschnitte durch Lesen der angefügten Zahlen ermitteln muss.
Abschreckendes Beispiel:
Medien-Meldungen über Aktienkurse oder andere Abläufe wie Corona-Infektionen und anderes. Alles ist automatisch auf komplette Platz-Ausnutzung skaliert, so dass man zwei Diagramme nicht direkt kiteinander vergleichen kann: Der eine Aktienkurs steigt in der Woche um 1 %, der andere um 25 %, aber beide Diagramme sehen gleich aus. Was soll’s also? Dann hätte man mit weniger Aufwand die Zahlen nennen können, bevor man sie aus den Achsen des Diagramms klauben muss. Man sieht: Ein Teil der Datenflut, die uns erreicht, beruht einfach auf der Dummheit der Daten-Übermittler, die sie zu sortieren nicht in der Lage oder willens sind.
Kluges Beispiel:
Man kann die Skalierung der Achsen dem Typ des Zusammenhangs anpassen, wenn der Nutzer damit umgehen kann. Bei exponentiellen Zusammenhängen nutzt man dann eine logarithmische Stauchung der Achse, um einen linearen Graphen zu erhalten. Dieser läuft dann nicht Gefahr, in jene Bereiche zu gelangen, wo Anstieg und Winkel einen optisch schlecht auflösbaren Zusammenhang bilden. ABER: Das Lesen solcher Graphen muss man geübt haben. (Für Physiker kein Problem, die das spätestens bei thermodynamischen Arrhenius-Ansätzen gelernt haben.)

Corona-Infektions-Zahlen linear dargestellt (5.4.20): Die Verlängerung der Verdopplungszeit muss man hier aus der Veränderung der Krümmung der Kurve ablesen, was durch die Tangens-Verfälschung der Geometrie steiler Kurven fast unmöglich ist (oder man liest die Zahlen gleich von den Achsen ab und rechnet im Kopf, als ob man eine Tabelle auswerten würde)
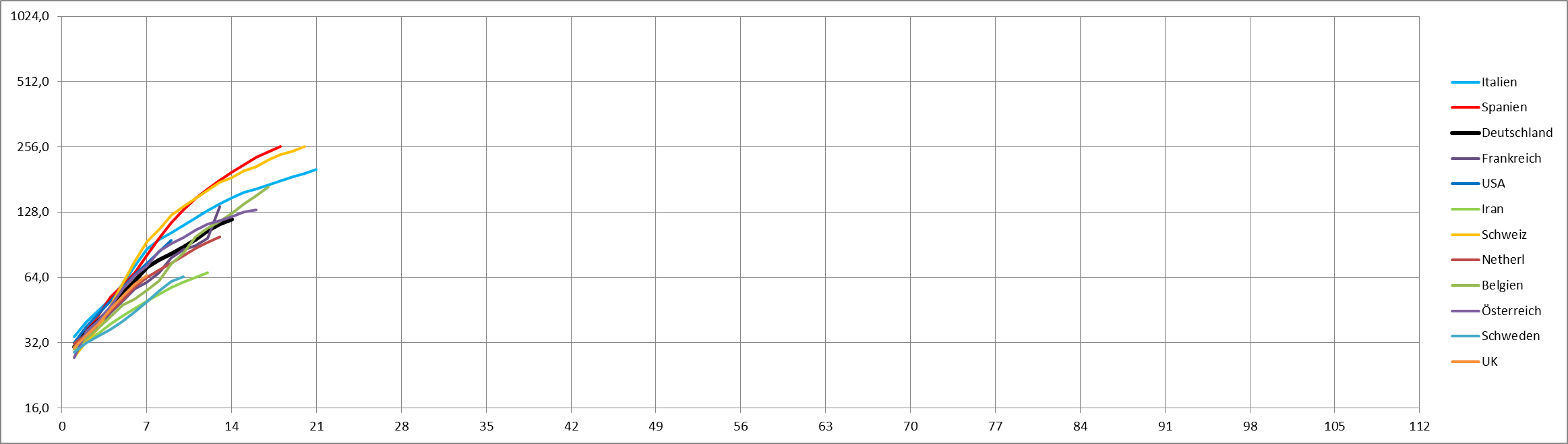
Corona-Infektions-Zahlen logarithmisch dargestellt (5.4.20): Man kann die Verlängerung der Verdopplungszeit am Flacherwerden der Kurven unmittelbar gut erkennen!
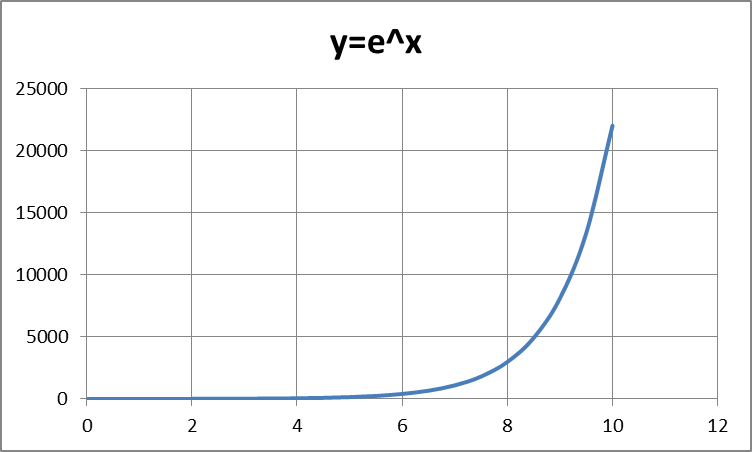
Der reine Exponential-Graph zeigt in linearer Skalierung die Tücke des Objekt besonders gut:
Der Graph sieht wie ein Bumerang (gerade – krumm – gerade) aus, dabei steigen mit zunehmendem Wert der Abszisse (x-Achse) nicht nur der Anstieg, sondern auch die Krümmung und die Änderung der Krümmung und… exponentiell an. Es ist die spezielle Eigenschaft dieser Funktion, dass ihr Anstieg, ihre Krümmung usw. und auch ihre unter der Funktion liegende Fläche alle gleich dem Funktionswert selber sind. Es sieht aus, als ob sie am Anfang „gleichmäßig flach“ sei und am Ende „gleichmäßig steil“, aber das ist die Täuschung der Darstellung.
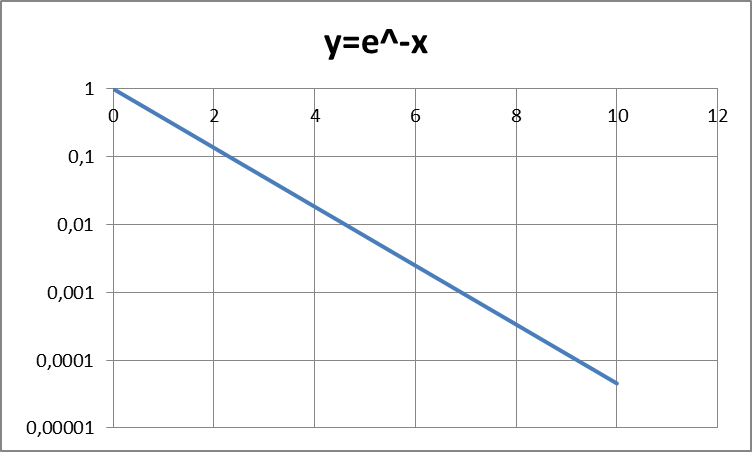
In logarithmischer Skalierung der Ordinate wird es übersichtlich:
Alle Werte sind die gleichen wie oben. Am konstanten Anstieg dieses Graphen erkennt man nun die konstante „Verdopplungszeit“ viel besser!
Genauso ist es beim Abklingen von etwas, wie zum Beispiel der Radioaktivität oder beim Temperatur-Ausgleich:
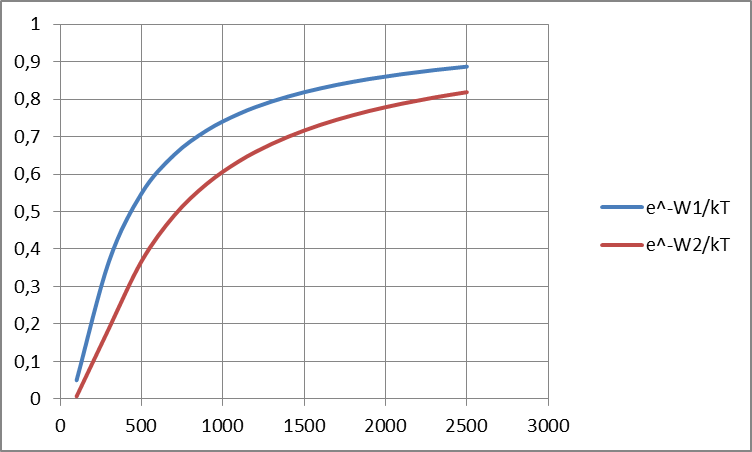
Hier noch ein nicht jugendfreier Spezialfall:
Wenn bei chemischen Prozessen oder Teilchen-Leitungs-Prozessen (Halbleiter-Elektronik) Anregungsenergien aufgebracht werden müssen, arbeitet man mit dem Arrhenius-Ansatz, nach welchem die Kinetik einer Exponentialfunktion entspricht, in deren negativem Exponenten die Temperatur im Nenner steht. Um den wesentlichen anderen Faktor des Exponenten, die im Zähler stehende Anregungsenergie grafisch ablesen zu können, stellt man das lineare Diagramm entsprechend um:
Die Abszisse (Temperatur) wird reziprok dargestellt und die Ordinate (Wahrscheinlichkeit oder Stromdichte oder Reaktionsgeschwindigkeit) logarithmisch. Das sieht dann im Vergleich mit gleichen Werten so aus:
Alles klar? (Übungsaufgabe: nachrechnen!!!)
FAZIT:
Diagramme sind eine gute Sache, wenn man sie zu lesen gelernt hat und ihre versteckten Tücken kennt, so dass man nicht auf die heute gängigen Automatisierungen hereinfällt. Die logarithmische Darstellung ist immer dann sinnvoll, wenn die darzustellenden Werte mehrere Zehnerpotenzen überstreichen.