2.8.3.5 Die „Schleifen“ der äußeren Planeten des Sonnensystems
Kann man in wenigen Schritten berechnen, wie der Mars seine Schleife am Nachthimmel zieht? Machen das auch andere Planeten?
Diese Frage stellt sich im Januar 2025 sehr deutlich, da es viele frostklare Nächte gab, in denen man sogar mitten in der Großstadt erkennen konnte, dass die „Linksbewegung“ des Mars (in der Fachsprache heißt das „rechtläufig“ im Sinne von „richtig läufig“ im Gegensatz zu „rückläufig“), ausgehend von der Konjunktion mit Jupiter vor wenigen Monaten, plötzlich in eine „Rechtsbewegung“ (also „rückläufig“) umschlug. Dabei halfen die beiden großen Sterne der Zwillinge, Castor und Pollux, bei der Beobachtung: Nachdem der Mars deren Verbindungslinie am Abendhimmel unterhalb von ihnen von rechts nach links überschritten hatte, steht er jetzt (22.1.25) wieder rechts davon, aber dichter dran. (Man hätte in eine Hand-Zeichnung der Sterne immer wieder die Positionen einzeichnen und dann die Punkte zu einer Kurve verbinden sollen…)
Nebenbemerkung: Die „Bewegung“ des Mars ist aus Sicht der Erde relativ zum Fixsternhimmel gemeint, also unabhängig von der täglichen Rotation der Erde! Und da wir als Normalsterbliche alle Beobachtungen von der Erde aus machen, ist das „nichtrotierende geozentrische Koordinatensystem“ also das, in welchem unsere Berechnungen von beobachtbaren „Bahnen“ also stattfinden müssen. Das erfordert eine Umrechnung der heliozentrisch zu berechnenden Daten! Diese sind ihrerseits nicht so einfach zu erlangen, wie wir gleich sehen werden.
Hinweis zum Einarbeiten: Wer mit einfacheren Beispielen anfangen will, der sei auf den Abschnitt „Symmetriebruch“ in den mathematischen Grundlagen hingewiesen.
Eine grobe Vereinfachung („nullte Näherung“ würde der Physiker sagen) des kosmischen Vorgangs erhält man, wenn man die Bahnen von Mars und Erde als kreisförmig (also mit jeweils konstanter Geschwindigkeit durchlaufen) annimmt und sie in die gleiche Ebene (Ekliptik) legt. In dem Zeitfenster, in welchem die Erde den Mars innen überholt, scheint dieser sich rückwärts (auf der Nordhalbkugel der Erde also nach rechts) zu bewegen.
Um das numerisch zu erledigen, geht man am besten von einer Situation mit hoher Symmetrie aus, also einer Konjunktion (von der Sonne aus Konjunktion, von der Erde aus Opposition), wo Sonne, Erde und Mars auf einer Geraden liegen, die zur x-Achse erklärt wird. (Bei zwei Kreisbahnen sollte also eine zeitliche Spiegelung der Bewegungen um diese Situation möglich sein.)
Den Winkel der Verbindungslinie Erde-Mars bezüglich dieser in der Ekliptik-Ebene festgelegten Geraden kann man dann schrittweise im Zeittakt berechnen, indem man jeweils beide Planeten-Positionen einzeln im heliozentrischen System berechnet (Radius der Kreisbahnen und Umlaufzeit – siderisch! – und somit Winkelgeschwindigkeit sind für beide bekannt) und über den Arkustangens den zeitabhängigen Erde-Mars-Winkel (betaM) bestimmt.
betaM(t) = arctan((yM-yE)/(xM-xE))
Dieser Winkel ist dann der Winkel-Abstand des Mars auf der Ekliptik vom Startpunkt auf der Konjunktionsgeraden (Schnitt dieser Geraden mit der Himmelskugel).
Man sieht, wir rechnen hier immer im heliozentrischen System die Positionen aus und geben dann im geozentrischen System die Himmelsposition an, denn wir wollen ja unsere Beobachtungen, die wir natürlich von der Erde aus (also geozentrisch!) tätigen, mathematisch nachvollziehen.
Die kartesischen Koordinaten im heliozentrischen System berechnen sich dann wie gewöhnlich aus den Polarkoordinaten nach
xM = rM*cos(wM*t) mit wM=2*pi/TM
(TM ist die Marsumlaufzeit, wM seine Winkelgeschwindigkeit rM sein Bahnradius und xM, yM seine kartesischen Koordinaten; das gleiche gilt auch für die Erde und für weitere Planeten, die man auf der Startlinie versammeln kann; t ist wie immer die Zeit)
Das Ergebnis ist richtig ästhetisch, sobald man sich in das Diagramm eingelesen hat:
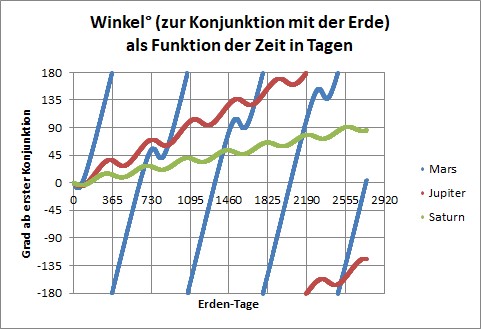
Geozentrische Bewegung der Planeten Mars, Jupiter und Saturn bei „gemeinsamem“ Start
Was erkennt man da nun?
Am einfachsten ist die grüne Saturn-Kurve zu verstehen: Der Saturn wandert (mit Blick aus Nord) im Mittel links herum auf der Ekliptik, was bei unseren Festlegungen ein Wachsen seines Winkels bedeutet, also geht die Kurve nach oben. „Vor ihm“ zappelt die Erde aber auf ihrer eigenen Kreisbahn hin und her, weshalb der Saturn vor dem hintergrund der Himmelskugel in die Gegenrichtung zu zappeln scheint, was auf der Kurve ein Auf-und-Ab bedeuten muss, was man tatsächlich wunderbar erkennt. Nach knapp 29 Überholvorgängen sollte die grüne Kurve um 360 Grad angestiegen sein (also dann von -180° wieder zu 0° gelangen) und dabei ihre Maxima langsam und in gleichen Schritten insgesamt um ein ganzes Jahr nach rechts versetzt haben, was dann die knapp 30 Erden-Jahre Saturnumlauf ergibt (wie überholen den Saturn immer erst nach einem reichlichen Jahr, weil er uns ein kleines Winkelstück (360°/30 = 12°) davongeeilt ist).
Beim Jupiter passiert das Ganze in knapp 12 Jahren, die Kurve ist also deutlich steiler.
Beim Mars passiert der Überholvorgang erst etwa aller zwei Jahre, weil er eine viel höhere Winkelgeschwindigkeit als die beiden Riesen hat, weshalb wir auf der Erde länger brauchen, bis wir wieder mit der Sonne und ihm auf einer Linie sind.
Fragen wir mit einem kleinen VBA-Programmchen den „Schleifenwinkel“ und die „Schleifen-Rücklaufzeit“ ab, kommen wir beim Mars auf etwa 15,9° und 74,1 Tage.
Das differiert etwas von den tatsächlichen Werten, die ja auf Ellipsen mit entsprechend veränderlichen Geschwindigkeiten beruhen. Geometrisch vor der Himmelskugel kommen dann sogar echte „Schleifen“, also sich selbst überschneidende Kurven, zustande, da sich nicht beide beteiligten Körper in derselben Ebene bewegen (siehe Neigung der Planetenbahnen gegen die Ekliptik).
Die hier entstandene Fehlergröße beim Mars erkennt man am besten an der sich ergebenden synodischen Umlaufzeit, die sich hier für den Mars mit 790 statt der richtigen 780 Tage ergibt, also nur bei etwas über 1 % liegt.
Das tatsächliche Bild der diesjährigen Schleife sieht am Himmel etwa so aus:
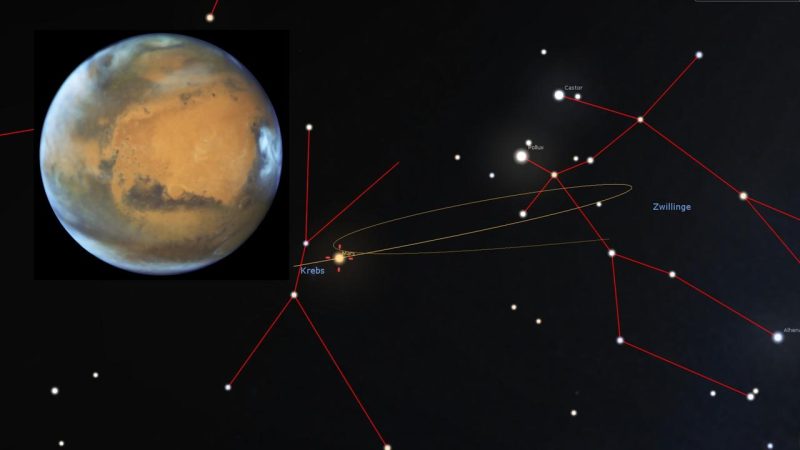
Marsschleife Anfang 2025: Die eingezeichnete Position entspricht dem Ausang aus der Schleife Anfang Mai nach links.
Quelle entnommen am 22.01.2025: https://www.deutschlandfunk.de/sternzeit-7-dezember-2024-der-mars-im-rueckwaertsgang-dlf-6432ec13-100.html
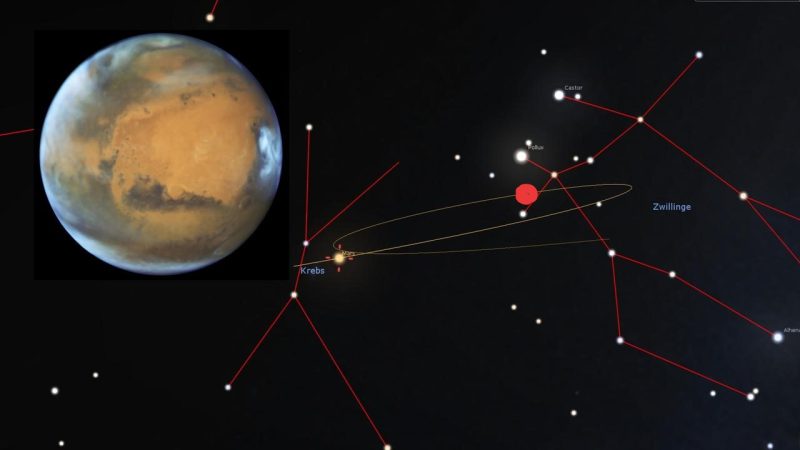
Hier habe ich ROT die am (21.01.2025) beobachtete Position eingezeichnet.
Wenn man weiter entfernte Objekte (Fixsterne) als Objekte in einem 3D-Raum auffasst, kann man mit ihrer gegenseitigen Winkelverschiebung während eines Erdenjahres auf ihre Stapelung in der Tiefe schließen und sukzessive ihre Abstände berechnen, solange die Auflösung der Teleskope es zulässt. Die Funktionskurven ihres zeitabhängigen Winkels sind dann – als genäherte Projektion einer Kreisbewegung der Erde – Sinusfunktionen mit sich etwa umgekehrt proportional mit der Entfernung verhaltender Amplitude.
Das wäre also eine schöne Hausaufgabe, diese Amplitude als „seitlichen Verschiebungswinkel“ vor der „Himmelskugel“ z.B. für den Sirius zu bestimmen! (…und zuerst als allgemeine Funktion des Abstandes zu formulieren…)
Aber nun wollen wir ja versuchen, die tatsächlichen Himmelspositinen im geozentrischen System zu berechnen und zu sehen, ob wir auf eine Rückläufigkeit vom 7. 12. 2024 bis 24.2.2025 mit dem „echten“ Himmelsbild kommen. Wir könnten es schrittweise machen, wie es auch Johannes Kepler getan hat:
Schritt 1: konstante Geschwindigkeit auf Kreisbahnen (erledigt: stimmt nicht mit der Realität überein)
Schritt 2: konstante Geschwindigkeit auf exzentrischen Kreisbahnen (stimmt immer noch nicht)
Schritt 3: konstante Geschwindigkeit auf Ellipsen (immer noch eine geringe Abweichung)
Schritt 4: veränderliche Geschwindigkeit auf Ellipsen: stimmt nur dann exakt, wenn man den Flächensatz (eine Kepler unbekannte Konsequenz der Drehimpulserhaltung) verwendet
(Das Ganze allerdings in 3D, nicht wie oben in einer einzigen Ebene der Ekliptik…)
KEPLERs Leistung ist also riesig, er hat viele Jahre lang probiert, bis es geklappt hat.
Wir wollen hier NICHT mit mathematischen oder experimentellen (aus der Beobachtung) Tabellen der Ellipsen-Bewegung im Schwerefeld arbeiten, sondern mit den beiden NEWTONschen Gesetzen der Gravitaion und der Trägheit die Planetenbahnen durch Integrieren ermitteln, wenn uns Anfangswerte für Ort und Geschwindigkeit gegeben sind. Dann sollten echte Raum-Zeit-Zusammenhänge darstellbar sein, die wir dann auf die Himmelskugel projozieren!
(Anmerkung: Selbst wenn wir einfach alle geometrischen 3D-Parameter der Mars- und der Erd-Ellipse irgendwo leicht finden könnten, hätten wir noch nicht die zeitliche Bewegung auf ihnen!)
Folgende Schritte scheinen vernünftig zu sein:
1. Festlegung eines geeigneten Koordinatensystems
2. Suche nach Konstellationen, aus denen die geforderten sieben Anfangsbedingungen (3 Orts- und 3 Geschwindigkeits-Komponenten zu einem (3+3+1=7) gemeinsamen Zeitpunkt) pro Planet ableitbar sind.
3. Integration der Newtonschen Gesetze im heliozentrischen System unter Verwendung der Massen der drei Körper und unter Vernachlässigung der Wechselwirkung zwischen den Planeten selbst (sonst müsste man außerdem mindestens Jupiter und Venus unbedingt hinzunehmen, das wäre eine weitere Präzisierungsidee für die Zukunft!)
4. Ermittlung der geozentrischen Himmelsposition des Mars (ekliptikal) und Vergleich mit bekannten Sternen (z.B. Castor und Pollux) nahe der 2024/25-er Schleife
zu 1. Festlegung des Koordinatensystems
Wir rechnen (integrieren) in kartesischen Koordinaten und transformieren die Ergebnisse dann auf die Kugelkoordnaten des Himmels. Wir nehmen die Erdbahnebene (Ekliptik) als x-y-Ebene, auf der die z-Achse senkrecht steht. Die x-Achse soll zum Frühlingpunkt des Ekliptik-Großkreises der Himmelskugel zeigen (auf dieser kommen wir also mit den beiden Winkeln der Kugelkoordinaten aus, die ebenfalls den Frühlingspunkt nutzen).
Die Erdbahn verläuft also definitionsgemäß komplett in der x-y-Ebene (vereinfacht zu 2D), die Sonne steht im Ursprung. Die Marsbahn ist gegen die Eklipitk geneigt, woraus sich eine 3D-Rechnung für die Bahn ergibt.
(Anmerkung: Wie haben unsere Vorfahren den Frühlingpunk im Sternenzelt gefunden, wenn die Sterne in Sonnennähe schließlich nicht zu sehen sind? Selber nachdenken!)
Ganz allgemein geht es also um das folgende in der Grafik (Handzeichnung) dargestellte Problem:
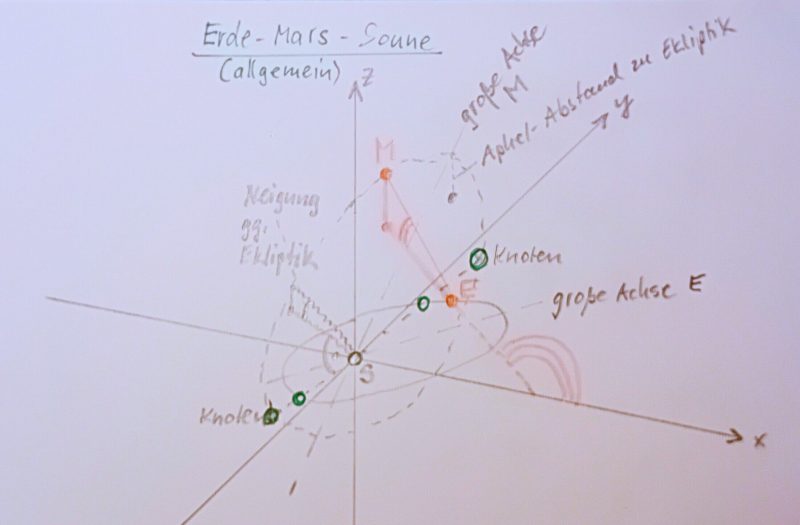
Koordinaten zweier Ellipsen
Berücksichtigt sind folgende Vereinbarungen und logische Zusammenhänge:
– die Sonne S liegt im Brennpunkt beider Ellipsen, wenn die Massen von Erde und Mars je vernachlässigbar sind gegen die der Sonne
– die Erdbahn-Ebene (Ekliptik) wird als kartesische x-y-Ebene definiert, in deren Ursprung die Sonne steht
– eine Richtung in dieser Ebene wird als x-Achse festgelegt (Frühlimgspunkt der Sonne)
– die große Achse der Erdbahn hat eine eigene Richtung
– die Marsbahn ist gegen die Ekliptik geneigt
– die Marsbahn hat eine eigene große Achse (Größe und Richtung)
– die Marsbahn hat Schnitte mit der Ekliptik, „Knoten“ genannt (grün gezeichnet)
– zu einem gegebenen Zeitpunkt schneidet die Verbindungsgerade von Erde und Mars die „unendlich“ weit weg gedachte Himmelskugel (deren Radius als im Vergleich zum Abstand Erde-Mars sehr groß sein soll) unter zwei Kugelkoordinaten-Winkeln (in der Skizze ROT eingezeichnet), mit deren Hilfe auch Sternörter angegeben werden, womit eine „Bahn“ vor dem Sternenzelt angebbar wird!
Zwei Fragen tauchen sofort auf:
– Recherche: Woher all diese Daten nehmen, wenn sie nicht in den üblichen Tabellen für Planeten des Sonnensystems enthalten sind? Siehe unten!
– Physik: Liegt die Sonne notwendig auf der Knotenlinie eines Planeten? Ja, denn: Zwei Ebenen (beide Planetenbahnen sind in erster Näherung eben: Drehimpulserhaltung) schneiden sich stets in einer Geraden. Ein Punkt, der notwendig zu beiden Ebenen gehören muss, weil er gleichzeitig Brennpunkt für beide Ellipsen sein muss, kann also nur auf dieser Geraden liegen. Da auch beide Knoten als Schnitte definiert sind, liegen alle drei Punkte auf einer Geraden, nämlich genau der Schnittgeraden, die also mit der Knotenlinie identisch ist. Aus der Kenntnis eines Knotens kann also auf die Lage des zweiten geschlossen werden, so wie aus der Lage des Aphels auf das Perihel geschlossen werden kann, was wir beides unten nutzen wollen.
zu 2. Anfangsbedingungen für die Integration
Das ist schon etwas schwieriger! Die pauschalen Daten wie Perihel und Aphel, Umlaufzeit und Bahnneigung oder Exzentrizität nutzen nicht viel, wenn man nicht weiß, wo die Knoten einer geneigten Bahn liegen (oder: in welche Richtung also die Neigung der Bahn zeigt). Aber wie immer überlegt man in der Physik, ob man aus Symmetrien der Konstellation Vereinfachungen ableiten kann, wenn einzelne Daten zur Verfügung stehen, wie bei Wikipedia spezielle Planeten-Konstellationen (https://de.wikipedia.org/wiki/Marspositionen):
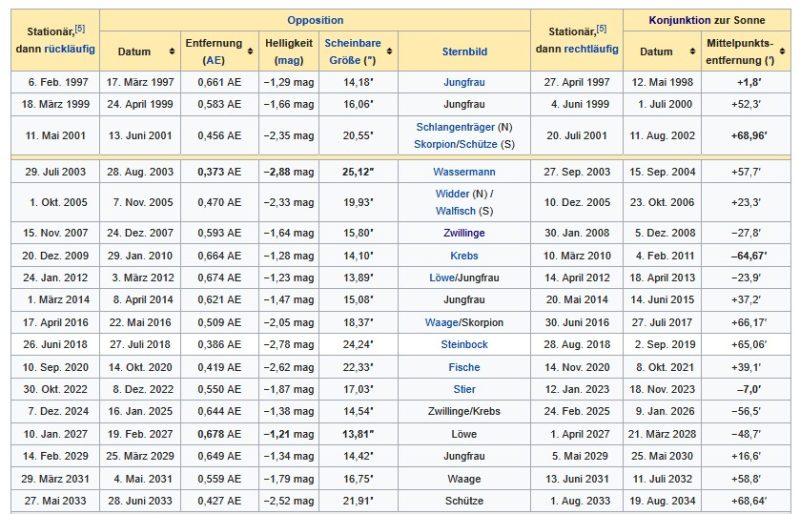
Mars-Positionen bei Wiki
Wir versuchen es mit 4-stelliger Genauigkeit:
Erde:
Perihel am 3. Januar (Perihelwinkel wEp = 102,9°) mit Perihelradius rEp=147,1 Mio km und Perihelgeschwindigkeit vEp=30,29 km/s (abgeleitet aus: https://de.wikipedia.org/wiki/Erde)
Symmetrie: im Perihel und Aphel steht die Geschwindigkeit senkrecht (!!) auf dem „Fahrstrahl“, ihre Komponenten sind also leicht zu ermitteln:
xEp = rEp * cos(wEp) = -32,93 Mio km; vEpx = – vEp * sin(wEp) = -29,52 km/s
yEp = rEp * sin(wEp) = 142,37 Mio km; vEpy = – vEp * cos(wEp) = -6,78 km/s
oder: Aphel am 5.7. mit 152,1 Mio km und 29,29 km/s
Symmetrie: Das Aphel müsste gegenüber bei -77,1° sein, was also im ersten Integrations-Test exakt herauskommen müsste! (Es ergeben sich aber bei meiner numerischen Integration -76,1°, was aber im Rahmen der Genauigkeit der Ausgangsdaten liegt, auch Aphel mit 152,25 Mio km und Geschwindigkeit mit 29,265 km/s liegen etwas (je 1 Promille) neben den Internet-Daten…)
Die eigene Probe über den Energiesatz-Vergleich von Aphel und Perihel (Abstand in potentieller Energie, Geschwindigkeitsbetrag in kinetischer) ist hinreichend genau.
Die Grafik zeigt natürlich annähernd einen Kreis für die Erdbahn, da die Exzentrizität sehr gering ist. Die oben angeführten Werte sind aus der Excel-Tabelle (mit 20.000 Zeilen für die Integrationsschritte) entnommen.
Das Procedere der numerischen Integration kann also erst einmal als sinnvoll und stimmig angesehen werden. Also nun der Mars!
(Hinweis: Nicht alle Daten auf Internetseiten sind wirklich gegengerechnet, sondern nur irgendwo abgeschrieben, wie eine Prüfung über den Energiesatz (Summe von potentieller und kinetischer Energie muss im Umlauf konstant bleiben) ergibt, bei der schon einmal 5% Energie-Abweichung zwischen Perihel und Aphel vorkommen können… Also: „Selber rechnen macht fi(et)t“!)
Mars:
Bahnneigung 1,85°, Opposition z.B. am 16.1.2025 (hier und im folgenden aus obiger Wiki-Tabelle)
Die Knoten der Marsbahn (Schnitte mit der Ekliptikebene) ergeben eine „Knotenlinie“, die notwendig die Sonne (also einen der beiden Brennpunkte der elliptischen Bahn) enthalten muss. Führt man eine „numerische Exzentrizität der Knotenlinie“ ein, so muss diese kleiner sein als (maximal gleich) die numerische Exzentrizität der Marsbahn, je nach Winkel zur Apsidenlinie (rechtwinklig zu dieser wäre sie Null).
Aus verschiedenen Ereignissen der Vergangenheit können wir auf die Lage der Knotenlinie schließen, z.B.: 18.11.2023 Konjunktion zur Sonne mit 7 Winkelminuten Ebenen-(„Mittelpunkt“-)Abweichung. Da für unseren angestrebten Beobachtungszeitraum jegliche Präzessionen unberücksichtigt bleiben sollen, können wir also die Lage der Knotenlinie im Raum auf der Ekliptikalebene festlegen: etwa 4 Erden-Monate vom Frühlingspunkt entfernt. Ob das der aufsteigende oder absteigende Knoten ist, können wir am Ende am Schleifenbild feststellen und diese Vorzeichen-Variable vorläufig frei lassen. Oder wir gehen mutig vom jetzigen (12.2.2025) Stand des Mars oberhalb der Ekliptik (etwa 4°) aus und sagen, das muss vor 15 Monaten (mehr als eine halbe Mars-Umlaufzeit) der absteigende Knoten gewesen sein. Daten: (https://de.wikipedia.org/wiki/Marspositionen)
Oppositionen 18.12.2022 und 16.01.2025
Konjunktion 18.11.2023
Die Knotenlinie scheint also ungefähr senkrecht auf der Apsidenlinie (=große Achse zwischen Wassermann und Löwe) zu stehen, also etwa zwischen Stier und Scorpion.
Würden wir mit mathematischen 3D-Ellipsen-Parameter-Darstellungen nur die Geometrie ermitteln wollen, könnten wir mit den Konstanten spielen, bis das Bild stimmt. Wir wollen aber einen „echten“ Zeitablauf über die Newtonschen Gesetze modellieren und müssen deshalb einen weiteren freien Parameter neben dem Knotenwinkel einführen, nämlich die z-Geschwindigkeit im Knoten, falls wir diese nicht über komplizierte Berechnungen als Funktion des Knotenwinkels herleiten wollen. (Mal sehen, ob dieses Konzept aufgeht…)
Perihel Mars rMp = 206,62 Mio km, vMp = 26,50 km/s; Wassermann (-25° ekliptikal); Aphel Mars rMa = 249,23 Mio km, vMa = 21,97 km/s (energetische Probe erstaunlicherweise sogar auf 6 Stellen genau!)
aufsteigender Knoten im Stier: 65°
Daraus leiten wir folgende Daten ab, die wir für die numerische Integration in den gewählten kartesischen Koordinaten benötigen:
| Stammdaten | |||
| Peri | Apo | aufst Kn | |
| rKM Miokm | 206,62 | 249,23 | |
| vKM km/s | 26,50 | 21,97 | |
| EkliWinkel ° | -25 | 155 | 65 |
| Neigung ° | 1,85 |
| abgeleitete Daten | |||
| Peri | |||
| xMp | 187,261315 | vMpx | 11,1993839 |
| yMp | -87,3213852 | vMpy | 24,0171564 |
| zMp | 6,04535348 | vMpz | 0 |
Probe: Die eingestellte z-Komponente der Mars-Geschwindigkeit in einem frei gewählten Startpunkt sollte dann die richtigen Knotenlagen ergeben. Erst dann wird die Schleife im „Sternenbild“ einigermaßen richtig erzeugt.
Für die richtige Synchronisation beider Bahnen (Erde und Mars) muss das Datum das Integrations-Startpunktes genau vorgegeben sein, damit die Übertragung ins geozentrische Bild Chancen auf Wahrhaftigkeit haben kann! Aus dem bekannten Perihel vom 28.08.2003 leiten wir mit der Umlaufzeit von 687 Erden-Tagen nach 11 Umläufen ein Perihel am 05.05.2024 ab. Dort ist die z-Komponente der Geschwindigkeit Null, wenn die Knotenlinie senkrecht auf der Apsidenlinie steht.
Jetzt wird es spannend, was die numerische Integration der Newtonschen Gesetze ergibt:
1. Die beiden Bahnen in der Draufsicht vom 20.08.2024 bis zum 29.05.2025:
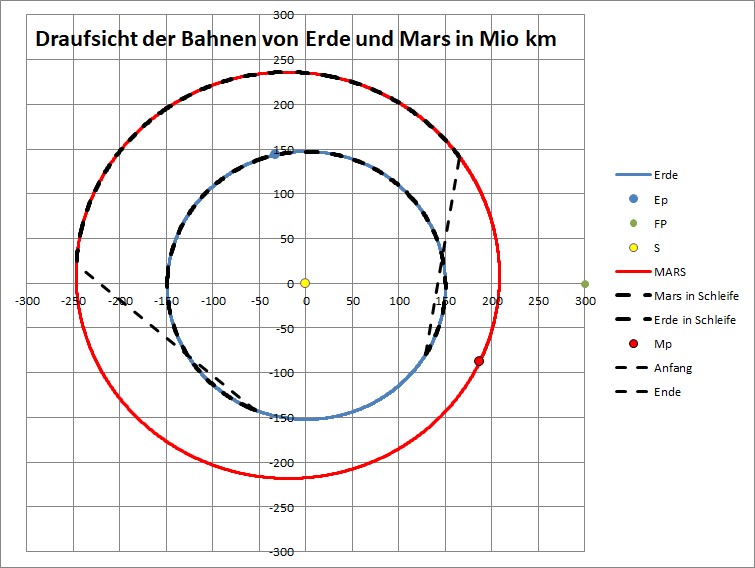
Draufsicht der Bahnen mit gestricheltem Beobachtungszeitraum und den Verbindungslinien am Anfang und am Ende (Ep und Mp sind die Perihels, S die Sonne und FP der Frühlingspunkt der Ekliptik)
2. Die Sicht von der Erde auf den Mars im Zeitablauf mit den Zwillingen im Hintergrund
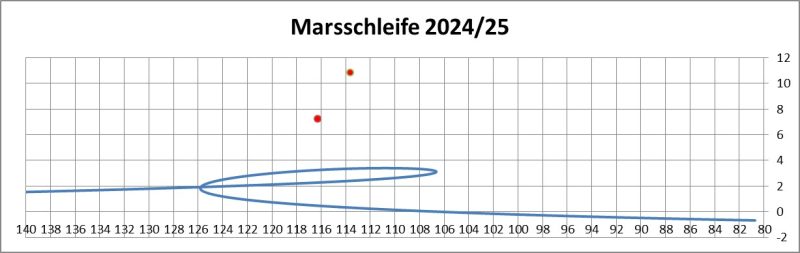
Berechnete Bahn vorm Sternenhimmel von der Erde aus vom 20.08.2025 bis 29.05.2025
Zusätzlich eingezeichnet sind die roten Punkte für Castor und Pollux, deren Daten man ebenfalls umrechnen muss:
Zwillinge (J2000.0)
Pollux: 7:45:19; 28°1,5′, also etwa 116,3° und 7,2°
Castor: 7:34:36; 31°53,3′, also etwa 113,6° und 10,9°
Die Lage der Ekliptik (oben die Abszisse des Diagramms) kann man grob vergleichen mit folgendem Bild:
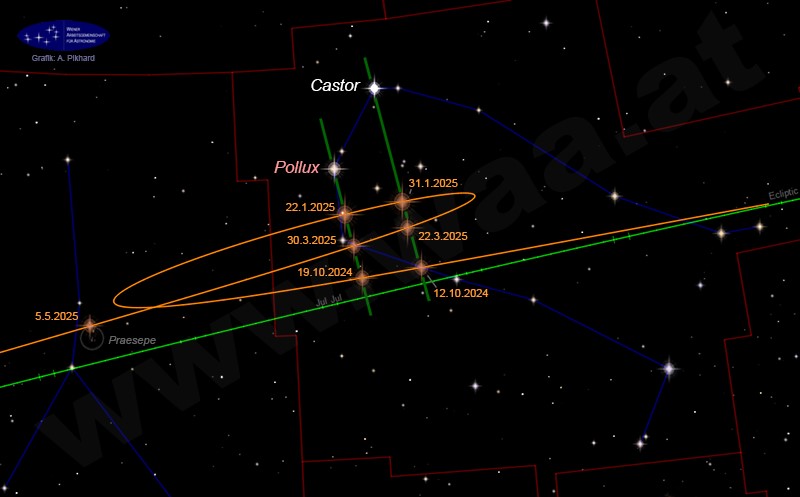
Marsschleife 2024/25 mit Zwillingen und Ekliptik (https://www.waa.at/hotspots/planeten/mars-2024-2025/)
Das Ergebnis ist beglückend genau und kann natürlich noch verbessert werden, wenn man die Daten verfeinert (auch die bisher nur grob geschätzten von Castor und Pollux!).
Im nächsten Schritt (wieder Hausaufgabe) kann das auch für den Jupiter (dessen Schleife wesentlich flacher ausfällt, da der Abstand größer ist…) wiederholt werden. Im Jahre 2026/27 werden beide Schleifen (Mars UND Jupiter) dicht nebeneinander stattfinden. Was sagt unsere eigene Hochrechnung im Vergleich mit https://www.waa.at/hotspots/planeten/mars-2026-2027/ dazu ??)
Kommentar abgeben