2.8.3.5.1 Grundsätzliches zur Planetenbahn-Berechnung
Zwei Grundsatzfragen:
1. Geometrie: Jeder weiß aus der Schule, dass es Ellipsen gibt und dass Planetenbahnen ebensolche Ellipsen sind. Manche wissen außerdem, dass Ellipsen Brennpunkte haben und dass im Sonnensystem die Sonne ziemlich genau im Brennpunkt jeder Planetenbahn steht. Wenige wissen auch, dass die Bahnen unterschiedlich geneigt sind. Geneigt wogegen?? Zum Beispiel gegen die Erdbahn-Ebene! Sind auch die Apsideninien oder die Knotenlinien gegeneinander verdreht??? Und wie stellt man das dar?
2. Kinematik: Selbst wenn man die jeweilige Ellipse geometrisch genau beschreiben kann, ist ihr zeitliches Durchlaufen damit noch lange nicht geklärt, das von der Erde aus sichtbare Himmelsgeschehen (Schleifen, Begegnungen der Planeten) schon gar nicht. Wie hilft man sich also???
Die beste Hilfe ist die Dynamik, also der Zusammenhang zwischen Kraft und Bewegung, also die beiden Newtonschen Gesetze zur Schwerkraft und Trägheit. Integriert man diese mittels der Kenntnis der Anfangsbedingungen (Zeitpunkt, Ortsvektor, Geschwindigkeitsvektor), so ergeben sich die Keplerschen Ellipsen von ganz allein, ohne dass man ihre Geometrie kennen muss. (Das Genauigkeitsmaß bei der Schließung der Ellipse sagt dann etwas über die Genauigkeit der numerischen Integrationsverfahren oder über die Zulassung von Störungen der Bahn durch Dritte – oder ein endliches Masseverhältnis im Zweikörperproblem – aus.)
Hinweis: Selbst die riesige und gut hergeleitete Formelsammlung zu Ellipsen-Darstellungen bei Wikipedia – https://de.wikipedia.org/wiki/Ellipse#Formelsammlung_(Ellipsengleichungen) – ist nicht hlifreich für die Kinematik, sondern reine Geometrie. Die Schwierigkeiten bei der Berechnung des Ellipsenumfangs weisen schon darauf hin, dass Zeitabläufe elliptischer Bahnen mit physikalischem Hintergrund nicht trivial sein können. Umso genialer ist Keplers Entdeckung des rein geometrischen Flächensatzes, dessen physikalischen Hintergrund (Drehimpulserhaltung) er nicht kennen konnte!
Mit diesen Gedanken können wir nun also getrost auf die Suche nach den passenden Anfangsbedingungen für die Integration gehen.
In Büchern und Internetseiten findet man schnell die allgemeinen Angaben für die Planetenellipsen wie Aphel, Perihel, mittlere Bahngeschwindigkeit, Bahnneigung und Exzentrizität (die sich teilweise auseinander ergeben), aber seltener die absoluten Lage-Parameter der angegebenen Ellipsen (d.h. relativ zur Erdbahn und zum Himmelsglobus). Dafür findet man häufig Hinweise auf benutzte Programme für Animationen, die man nicht selber geschrieben hat. Wenn man es aber wirklich verstehen will, muss man es selber rechnen können.
Ist es zum Beispiel das Ziel, Planetenschleifen zu berechnen, wie man sie am Himmel von der Erde aus selber sieht, so braucht man also komplette Daten für die folgenden Schritte:
a) Berechnung einer Planetenbahn im kartesischen R3 über doppelte Zeit-Integration der Keplergesetze bei bekannten Anfangsbedingungen
b) zeitliche Synchronisation unterschiedlicher Planetenbahnen
c) Transformation in geozentrische Kugelkoordinaten zur (zeitsynchronisierten!) Darstellung vor dem Himmelsglobus
Folgende Quelle habe ich unter
https://www.katharinengymnasium.de/wolf/web/Ellipse/EllipseKepler.html
gefunden:
| Venus ♀ | Erde ♁ | Mars ♂ | Jupiter ♃ | Komet Halley | |
| große Halbsachse a in AE | 0,7233 | 1 | 1,5237 | 5,2034 | 178.341 |
| numerische Exzentrizität ε | 0,00677 | 0,01671 | 0,09341 | 0,04839 | 0.96714 |
| Umlaufzeit T in a | 0,6152 | 1 | 1,8808 | 11,8626 | 75.32 |
| Inklination i | 3,3947° | — | 1,8506° | 1,3053° | 162.2627° |
| Länge Ω des aufsteigenden Knotens | 76,680° | 49,579° | 100,556° | 58.420° | |
| Argument des Perihels ω | 54,8523° | 286,4623° |
Für den Jupiter müssen wir das Argument des Perihels also noch selber finden, zum Beispiel aus den Jupiterdaten
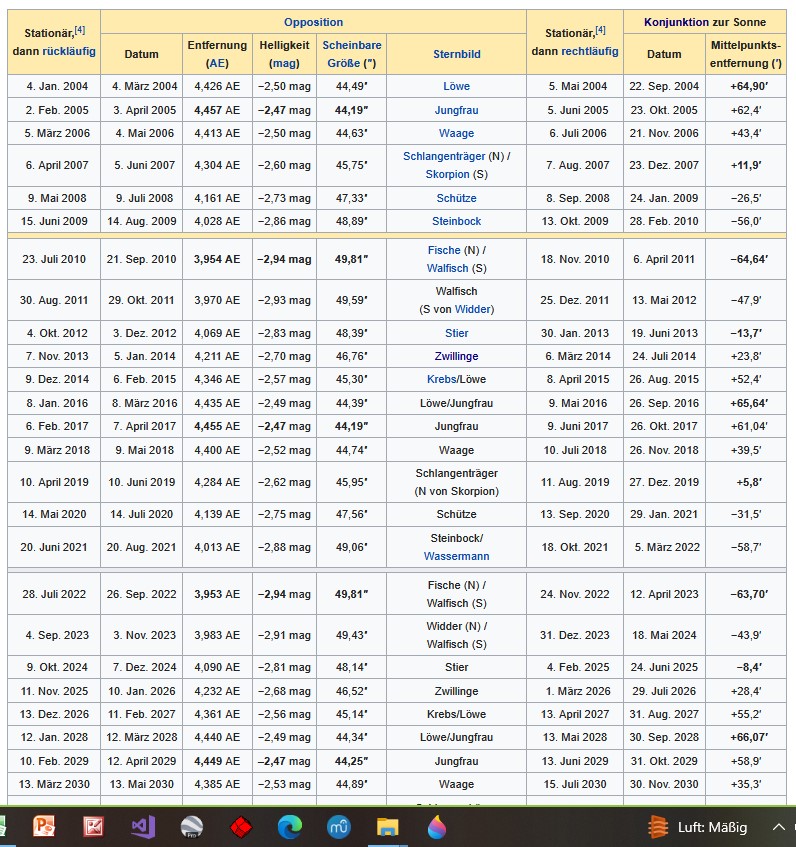
Jupiterdaten aus https://de.wikipedia.org/wiki/Jupiterpositionen
Wenn wir davon ausgehen, dass die größte Winkelabweichung von der Ekliptikebene im Perihel zu sehen sein sollte, so können wir die Konjunktionsdaten zur Sonne über einen großen Zeitraum verfolgen und die Maxima suchen, die laut obiger Tabelle positiv um den 26. September und negativ um den 10 April liegen. Vom Frühlingspunkt aus gerechnet wären das dann etwa 20°.
Im Vergleich zu den NASA-Daten
https://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html
Jupiter Mean Orbital Elements (J2000)
Semimajor axis (AU) 5.20336301 Orbital eccentricity 0.04839266 Orbital inclination (deg) 1.30530 Longitude of ascending node (deg) 100.55615 Longitude of perihelion (deg) 14.75385 Mean Longitude (deg) 34.40438
| Max. orbital velocity (km/s) | 13.72 |
|---|
| Perihelion (106 km) | 740.595 |
|---|
liegen wir also nicht sehr falsch (allerdings: anderes Bezugssystem in günstiger Epoche J2000.0!). Auch hier liegen die Knoten (wie beim Mars) etwa 90° verschoben, was bei der geringen Exzentrizität beruhigend ist.
Unsere erste Integration (EXCEL, damit jederzeit nachvollziehbar) wird zeigen, ob wir mit diesen Daten zu vernünftigen Ergebnissen kommen.
Kommentar abgeben