2.8.4.1 Rotierendes Bezugssystem
Kann man verstehen, warum die verwirrend klingenden „Scheinkräfte“ in bewegten (insbesondere in beschleunigt bewegten) Bezugssystemen das Verstehen erleichtern können?
Zwei solcher Kräfte treten dort ständig auf, wenn die Beschleunigung eine einfache Rotation (mit konstanter Winkelgeschwindigkeit) ist:
– die Zentrifugalkraft Fz („Fliehkraft“) als Gegenkraft („Scheinkraft“) der für das Festhalten eines Körpers an seinem Ort im mitrotierenden System erforderlichen Zentripetalkraft
– die Corioliskraft Fc als „Scheinkraft“, die einen sich eigentlich kräftefrei (also geradlinig gleichförmig) bewegenden Körper im rotierenden Bezugssystem zur Seite abzulenken scheint
Die Zentrifugalkraft spürt man an der Spannung des Fadens, wenn man einen Stein an seinem Ende rotieren lässt.
Die Corioliskraft spürt man, wenn man sich auf einer drehenden Scheibe (Mini-Karussell auf dem Spielplatz) bewegt: Man verliert das Gleichgewicht, wenn man sich an der drehenden Scheibe selbst orientiert und zum Beispiel von ihrem Rand zum Zentrum laufen will.
Interessant wird es dann, wenn man diese Kräfte mit anderen „mischt“, zum Beispiel in einem Schwerefeld.
In der Physik operiert man gern mit einem so genannten Potential, dessen Gradient der wirkenden Kraft proportional ist. Umgekehrt ist also das Potential ein Integral der Kraft (man erkennt daraus sofort, dass das Potential intervallskaliert ist, also einen frei wählbaren Nullpunkt hat).
Das gravitative Schwerepotential Pg der Schwerkraft Fg einer Punktmasse einerseits und die Schwerkraft selbst sind somit (mit positiven Konstanten Ci versehen) so darstellbar (das Minuszeichen steht in den skalaren Formulierungen für die Richtung der Kraft bezüglich wachsendem r):
Pg = -C1 * 1/r
Fg = -C2 * 1/r²
Erzeugt man auch für die Fliehkraft
Fz = m * ω² * r = m * v² / r
ein Potential, so hat das für konstantes ω die Form
Pz = -C3 * r²
(r: Radius; ω: Winkelgeschwindigkeit; m: Masse)
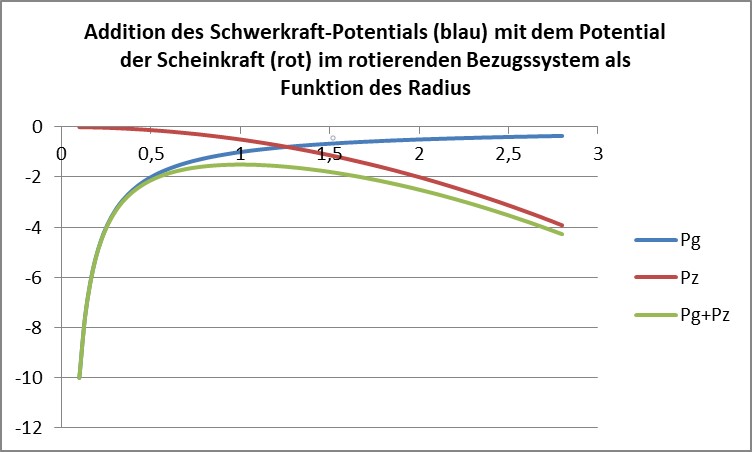
Beide Potentiale addiert („superponiert“) ergibt folgendes Bild:
Welchen „Sinn“ hat die Einführung der Potentiale?
Durch „animalische“ Alltags-Erfahrung kennen wir uns mit „Gebirgen“ aus, also mit gewölbten Oberflächen im Schwerefeld der Erde, und mit dem, was sie mit uns machen, wenn wir auf dieser „Unterlage“ sportlich rollen oder gleiten können! Diese Unterlage ist sozusagen ein Potential-Gebirge, an dessen Abhängen wir eine Beschleunigung nach unten spüren, nämlich in Richtung der „Fall-Linie“, was mathematisch die Richtung des Gradienten (vektorielle Ableitung des „Skalars“ Potential) ist.
Übertragen wir nun diese Alltags-Erfahrung auf das oben grün gezeichnete Potential, erkennen wir schnell, dass es da einen Berggipfel gibt, auf dem wir nicht wegrollen oder weggleiten. Das ist im rotierenden System nun jener Abstand, bei dem während der Rotation unser Abstand vom Mittelpunkt unverändert bleibt, wir also im ruhenden Bezugssystem einen Kreis beschreiben. In Physik haben wir gelernt, dass dort ein Kräfte-Gleichgewicht herrscht, nämlich jenes zwischen Zentrifugalkraft Fz und Zentripetalkraft Fg: die Anstiege der beiden Potentialkurven sind dort also entgegengesetzt gleich, ihre Summe bildet also einen lokalen Extremwert (oder einen horizontalen Wendepunkt). Hier ist es ein Maximum, von dem wie nach außen oder nach innen „abrutschen“ könnten.
In 3D-Ansicht sehen die Potential-Diagramme dann so aus:
Überlagert man die Summe von Gravitations- und Fliehkraft-Potential für einen symmetrischen Doppelstern, alos zwei gleich große Massen, erhält man folgendes Bild (links), für unterschiedlicheMassen ein entsprechend „schiefes“ (rechts):
(Das ist die Basis für die Abhandlung in 2.8.4 .)
Was passiert nun, wenn wir vom schmalen ringförmigen Potential-Maximum „abrutschen“?
Man sollte meinen, dass man dann entweder ins Schwerkraft-Zentrum stürzt oder ins Unendliche geschleudert wird! Wäre das ein statisches Potential, verhielte es sich genau so! Aber es ist ein „Schein-Potential“, in welchem auch die weitere „Scheinkraft“ Corioliskraft Fc wirkt, sobald eine Relativ-Geschwindigkeit v zu diesem Bezugssystem auftritt.
Fc = C4 * v x ω
Das „x“ steht hier für das vektorielle Kreuzprodukt. Das bedeutet, dass die errechnete Kraft senkrecht auf der durch die Geschwindigkeit v und die Winkelgeschwindigkeit ω (längs der Achse gerichtet!) gebildeten Ebene steht (Unterstriche sollen Vektoren bezeichnen!), also auf der Unterlage stets im gleichsinnig rechten Winkel zur Geschwindigkeit wirkt. Dadurch verändert diese Kraft den Betrag der Geschwindigkeit nicht (verrichtet also keine „Arbeit“) und führt dazu, dass sich die Masse auf einem Kreis bewegt, sofern nicht weitere Kräfte wirken können!
Interessanterweise ist diese kreisähnliche Kurve ähnlich jener, die eine gravitative Ellipse im konstant rotierenden Bezugssystem (mittlere Winkelgeschwindigkeit als 2π/Umlaufzeit benutzt) beschreibt! (Die elastische Ellipse beschreibt einen exakten Kreis im rotierenden System. Siehe unten!)
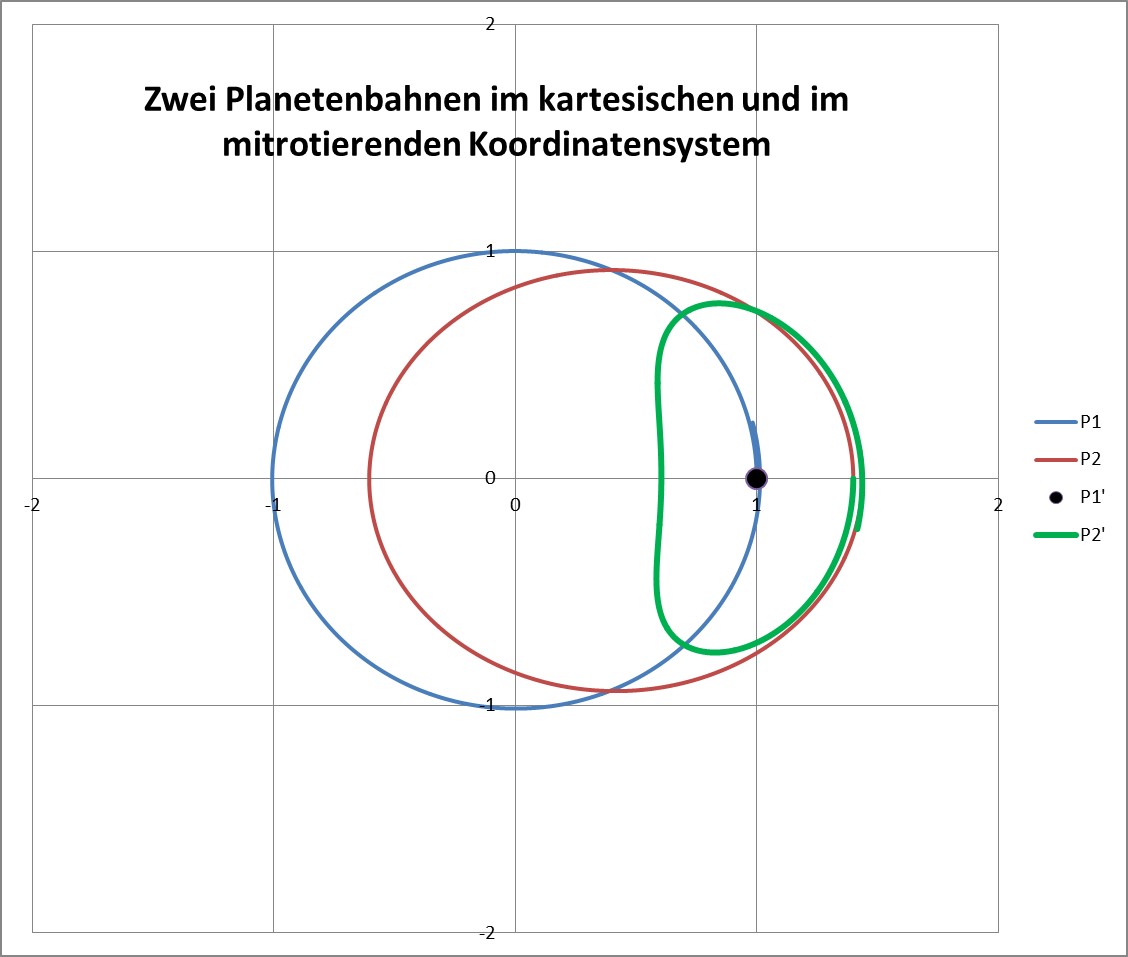
Ein auf einer elliptischen Bahn laufender Planet P2 würde sich also im Vergleich zu einem Kreisbahn-Planeten P1 (gleicher Umlaufzeit!) im mitrotierenden Bezugssystem auf einem Coriolis-Kraft-Kreis bewegen, wenn nicht die weiteren Potentialwölbungen (siehe oben!!) vorhanden wären! Durch diese wird der Kreis ein wenig zu einem (an den Schnitt eines roten Blutkörperchens oder Pantoffeltierchens erinnernden) nierenförmigen Kissen deformiert, wie eine numerische Integration mit etwa 6000 Stützstellen pro Umlauf zeigt. (Der Umlauf ist etwas überschritten, um die Größe der numerischen Artefakte sichtbar zu machen.)
Der Ellipsen-Planet P2 „überholt“ innen den Kreis-Planeten P1 und lässt sich dann „außen“ wieder zurückfallen. Da er dafür länger braucht, ist es eben im mitrotierenden System (mit Apostroph gekennzeichnet) kein exakter „Kreis“. P2′ beschreibt also das erwähnte „Kissen“ um P1′!
Je kleiner die Abweichung von der „wahren“ Kreis-Bahn ist, desto näher kommt auch die Bahnkurve im mitrotierenden Bezugssystem einem Kreise (erst wird sie fast eine Ellipse, dann ein infinitesimaler Kreis…).
So etwa kann man sich nun also die Bewegung der künstlichen Satelliten oder Asterioden in den Lagrange-Punkten der Systeme Erde-Sonne oder Erde-Mond vorstellen, in denen zusätzlich zur radialen Richtung auch azimutal ein lokales Extremum vorliegt, was in ihrer Nähe die Abweichung von kleinen Kreisbahnen in erträglichen Grenzen hält.
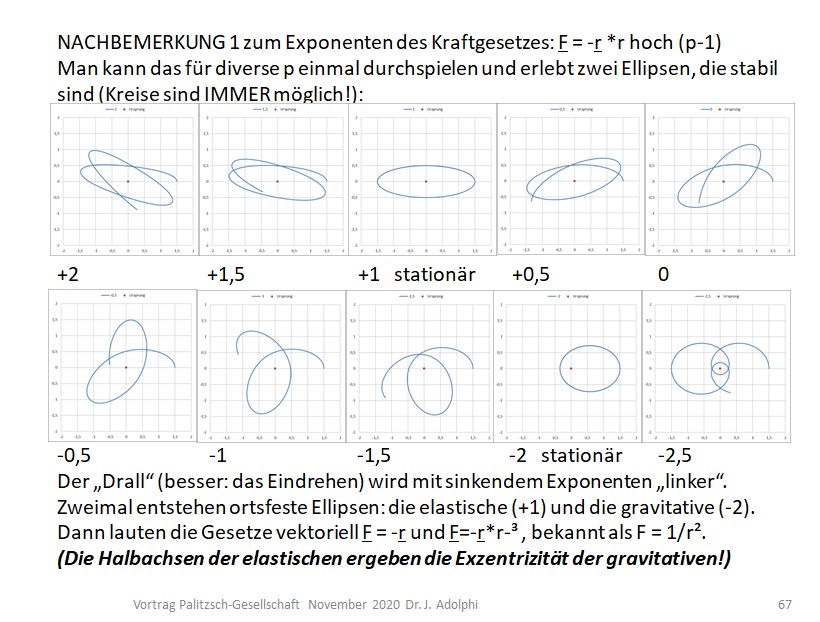
Heuristisch müssen wir uns aber auch hier wieder fragen, wie sich eigentlich der Unterschied zwischen gravitativen und elastischen Ellipsen-Bahnen auf das konstant rotierende Koordinatensystem auswirkt! Hier die Gegenüberstellung für noch exzentrischere Bahnen:
Der „grüne Kreis“ der elastischen Bahn (linkes Bild) wird bei einer Umdrehung zweimal durchlaufen, die „grüne Niere“ (rechtes Bild) nur einmal. Auch dies ist wieder ein Hinweis darauf, dass die gravitative Ellipse die niedrigste ganzzahlige „Vorwärts-Apsidendrehungsfrequenz“ besitzt (siehe dort: 2.8.3.2 Spiel mit der Kepler-Ellipse!):
Die (alle „linksdrehenden“) elliptischen Bahnen erreichen beim Exponenten -2 durch heftige Vorwärts-Apsidendrehung die erste „Vorwärts“-Überdeckung der beiden großen „elastischen“ Halbachsen.
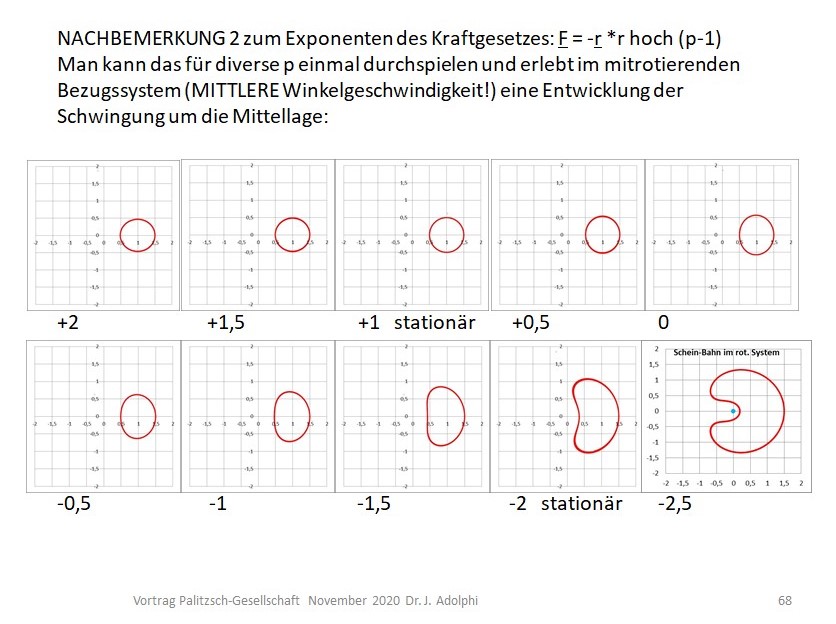
Im (mit der mittleren Winkelgeschwindigkeit) mitrotierenden Bezugssystem sieht diese Entwicklung dann so aus:
Hier noch die interessante Entwicklung des elastischen Kreises in Abhängigkeit von der Exzentrizität (Umlaufdauer elastisch stets physikalisch synchronisiert, da unabhängig von Schwingweite; Auswahl willkürlich für stets gleichgroße Große Halbachse der Vergleichsellipse)
im Gegensatz zum gravitativen Fall der Nierenform, ebenfalls in drei Ausprägungen:
(Hier ist die Synchronizität – im Gegensatz zum elastischen Fall – nur durch jeweilige Gleichheit der Großen Halbachse mit dem Kreisradius (Kepler!) zu erreichen. Andernfalls hätte man zwei unterschiedliche Winkelgeschwindigkeiten ansetzen müssen.)
Philosophisches FAZIT zu gravitativen Trajektorien:
- Die Bahnkurven im rotierenden Bezugssystem verraten uns etwas über die Stabilität der Zustände, denn sie zeigen eine verallgemeinerte Schwingung um einen Gleichgewichtspunkt, der allein durch einen Abstand definiert ist.
- Abstände sind verhältnisskalierte Größen, also absolut. Raumpunkte sind intervallskaliert, also relativ. Ob eine Bahnkurve eine raumfeste Keplersche Ellipse ist oder eine präzedierende Ellipse (Rosette), spielt im rotierenden System keine Rolle. Im sogenannten „ruhenden“ System ist die (stationäre!) Kepler-Ellipse somit eine zufällige Ausnahme, die sowohl an einen bestimmten Exponenten des Kraftgesetzes als auch an eine bestimmte Geometrie der Zentralmasse gebunden ist.
- Das Zwei-Körper-Problem kann auch bei abweichendem Kraft-Exponenten bzw. bei nicht kugelsymmetrischer Zentralmasse im rotierenden System wie ein Pendeln um einen Gleichgewichtszustand aufgefasst werden. Eine im zwei- oder dreidimensionalen Raum wirkende „rücktreibende Kraft“ kann über einen begrenzten Stabilitätsbereich (Gesamtenergie kleiner als Null) wirken. (Es existiert im übertragenen Sinne ein „Lagrange-Ring“).
- Im Drei-Körper-Problem (oder mit noch mehr Körpern) wird der Stabilitätsbereich um „Lagrange-Punkte“ immer kleiner, abhängig von der Masse-Verteilung auf die Teilnehmer und von deren Symmetrie.













Kommentar abgeben