4.2.1.1 Geometrie-Strukturelement 1: Punkt als Kreuzung
Der streng geometrische Punkt ist unsichtbar, weil er keine Ausdehnung hat. Wir zeichnen ihn gewöhnlich so klein wie möglich oder stilisieren ihn zum gefüllten Kreis oder zur gefüllten Kugel: ohne Vorzugsrichtung kollidiert er auf solche Weise nicht mit anderen Elementen.
Als Strukturelement kann er natürlich (sofern sichtbar) Strukturen bilden:

vorsichtig geschüttelte Stahlkugeln wechseln ihre Plätze in Richtung des potentiellen Energieminimums

Modellierung (205 Schritte) einer anisotropen und konzentrationsabhängigen 2D- Diffusion: Fluktiationen führen systematisch zu strichartigen Anhäufungen
Der streng geometrische Punkt kommt natürlich in seiner exponiertesten Form alsKreuzung von
- Linien (mindestens zwei im Zweidimensionalen)
- Flächen (mindestens drei im Dreidimensionalen)
- Räumen (mindestens vier im Vierdimensionalen)
usw. usf. und auch als „normales“ Element aller dieser höheren Dimensionen vor.
(Mathematisch wären das die Gleichsetzungen von 2 Geraden- oder anderen Funktionsgleichungen, 3 Ebenen- (…) gleichungen, 4 Raumgleichungen usw. usf.)
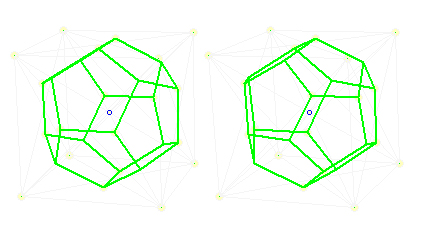
Pentagondodekaeder mit 20 Ecken als Kreuzungspunkte von je 3 der 12 Flächen oder 3 der 20 Kanten
Das bedeutet im Umkehrschluss:
Die Strukturierung einer Anzahl von Punkten (absichtlich nicht „Gruppe“ genannt) erfolgt durch Beziehungen, die über die Dimension des Punktes selbst hinausgehen müssen (da er eine „innere“ Struktur nicht haben kann), also durch strukturierte Abstände (gedachte „Linien“) und/oder Winkel zwischen diesen.
Lineare Punktmuster
Die denkbar einfachste Beziehung besteht zwischen zwei Punkten: Der Abstand. Das ist noch keine „Struktur“, da das Wesen der Wiederholung oder Variation o.a.m. fehlt.
Schon im eindimensionalen Fall können Punkte auf einer gedachten Geraden Rhythmen bilden.

Punkt-Struktur auf einer Geraden: Als „Werden“ dieser Struktur vermutet man „automatisch“ eine stehende oder laufende Welle von pendelartigen Schwingungen
Ebene Punktmuster
Zweimal zwei Punkte sind streng genommen auch noch keine Struktur von Punkten, sondern ein Paar von Strecken und das gehört nicht hierher. Ab drei Punkte können wir aber schon von Struktur sprechen (auch, wenn wir die zwei Punktpaare punktweise in Beziehung setzen). Dann können die drei möglichen gedachten Verbindungslinien Winkel zueinander bilden oder die drei Punkte zu ihrem Schwerpunkt (als gedachter vierter) in Beziehung treten. Das ist nie mehr als zweidimensional. Jeder weitere Punkt auf dieser Ebene erhöht die Zahl der Beziehungen. Am Ende könnte man das mathematisch (gruppentheoretisch) mit Symmetrieoperationen versehen, um „Strukturen“ systematisch zu „ordnen“.
Hier kann man auch sehr „ästhetische“ Figuren bilden, z.B. die auch die Vorstellungskraft herausfordern oder anregen: Welche Struktur („Muster“) bilden die Kreuzungspunkte der Diagonalen regelmäßiger n-Ecke? Man vermutet, dass alle wieder auf n-Ecken oder m*n-Ecken liegen müssten, die das Auge mit dem Kopf vielleicht zu Kreisen oder lokalen Gruppierungen abstrahiert? Wollen wir es probieren?

n ist ungerade beim 13-Eck, das Zentrum ist leer und auch ein 13-Eck

n ist gerade beim 14-Eck, das Zentrum ist ein 14-Stern aus den Mittelsenkrechten eines um pi/14 verdrehten 14-Ecks
Die Geraden stören richtig. Kriegt man sie weg? Da muss man dafür die Schnittpunkte berechnen, was etwas aufwändiger ist:

Huch?! Auch bei einem Denk- oder Schreibfehler im Programm kann es eine Struktur geben! Aus der Abweichung vom Erwarteten sollte man eigentlich auf den Programmierfehler schließen können! (Ein Gesicht hineingedacht und das ganze zum gebundenen Kopftuch im Wind oder mit Krause erklärt: hübsch!)

Die dazugehörigen Diagonalen des 23-Ecks

Die Schnittpunkte der Diagonalen des 23-Ecks nun richtg: Die Schachtelung der vier Schleifen zur Schnittpunktermittlung war fehlerhaft: Sie hatte einen einzigen Dreher.
Gibt man dem Punkt die außergeometrische Eigenschaft der Farbe, kann man mit dieser spielen und „Strukturen“ erzeugen. Hier ein Beispiel von 1000 x 1000 Punkten mit einer Farbvorschrift, die sich als Kombination der Koordinaten darstellen lässt:
Das ist hier „live“, und da passieren Leichtsinnsfehler: Die quadratische Struktur im linken Bild ist NICHT mit der Bildungsvorschrift der Farben zu erklären, denn man sollte Hyperbeln erwarten. Und siehe da: Im Rot-Anteil war das Produkt beider Koordinaten nur einmal durch 100 geteilt statt zweimal, und schon hat die schwebende Rundung der heftigen Sinusfrequenz zu artefaktischen Mustern geführt. GUT, dass solche Fehler auftreten, sie sind eine Warnung! Rechts das korrigierte Bild mit dem Teiler 100*100=10000 (Korrektur im Quelltext fett hervorgehoben).
For i = 1 To 1000
For j = 1 To 1000
farbe(i, j) = RGB(100 + Int(100 * Sin(i * j / 10000)), 100 + Int(100 * Sin(i / 100 + 1)), 100 + Int(100 * Sin(i / 100 + 2)))
Next
Next
For i = 1 To 1000
For j = 1 To 1000
Circle (2000 + 6 * i, 2000 + 6 * j), 6, farbe(i, j)
Next
Next
Räumliche Punktmuster, z.B. Kristalle
Für mich ganz persönlich ist das Objekt „Punkt“ aber spannender als Eckpunkt eines Kristalls (oder eines anderen, eben begrenzten Körpers wie denen der Architektur), in welchem mehrere Kanten zusammenlaufen, die ihrerseits wieder Schnitte von je zwei Ebenen darstellen, wodurch der Eckpunkt auch als Schnittpunkt aller dieser Ebenen aufgefasst werden kann.
Unter dem Gesichtspunkt der höchsten „nicht-strukturellen“ Forderung an alle Eckpunkte eines Kristalls, nämlich den gleichen Zentralabstand zu haben (also alle auf der Umkugel liegend), kann man sich fragen, wieviel Typen von Eckpunkten es eigentlich geben kann, oder anders ausgedrückt, wieviel kongruente regelmäßige n-Eck-Flächen können sich eigentlich in ihm schneiden?
Man merkt schnell, dass die Frage auch einfacher gestellt werden kann: Wieviele Kanten können von einem Punkt ausgehen, die untereinander den gleichen Winkel haben und zu regelmäßigen n-Ecks gehören?
In der Ebene ist die Lösung schnell gefunden: 6 Dreiecke, 4 Quadrate oder 3 Sechsecke.
Das ist dann aber keine 3-dimensionale „Ecke“!
Im Raum ist die Bedingung, dass die Summe der Innenwinkel der anliegenden Flächenecken kleiner als 360° sein muss. Das kennt man von Schnittmustern, von man einen „Keil“ aus einer Ebene ausschneiden muss, damit man den Rest zu einer Spitze wölben kann.
Die Lösung ist komplexer als in der Ebene:
3 Dreicke werden zur Tetraederecke (3*60°=180° < 360°)
4 Dreiecke werden zur Oktaederecke (4*60°=240° < 360°)
5 Dreiecke werden zur Ikosaederecke (5*60°=300° < 360°) (ein 6. ergäbe 360°)
3 Vierecke werden zur Würfelecke (3*90°=270° < 360°) (ein 4. ergäbe 360°)
3 Fünfecke werden zur Dodekaederecke (3*108°=324° < 360°) (ein 4. ergäbe mehr als 360°)
Wir sind also bei den „Platonischen Körpern“ gelandet. Für einen Kristall gibt es aber eine unverzichtbare Zusatzbedingung: Seine Elementarzellen müssen gestapelt werden können, was man mathematisch Translationsinvarianz nennt: Das Gitter muss bei einer Translation um ganze Elementarzellen in sich selbst übergehen. Da scheiden Ikosaeder und Pentagon-Dodekaeder aus!
Wenn wir aber zwei andere Zusatzbedingungen aufheben, nämlich dass alle Flächen regelmäßige n-Ecke sein sollen und dass alle Punkte auf der Umkugel liegen müssen, so erschließt sich uns die weite Welt der tatsächlich vorkommenden Kristalltrachten im weiten Feld der Kristallografie.
Fazit:
Als Struktur-Element kann der Punkt auf unterschiedliche Weise dienen oder „entstehen“. Er kann außerdem, wenn man ihn nicht mathematisch als unendlich klein ansieht, Eigenschaften unserer realen Welt wie Durchmesser und Farbe oder sogar Farbstruktur haben und hat dann meist die Form eines Kreises oder einer Kugel. Im übertragenen Sinne ist der Punkt auch ein Element grafischer Darstellungen von Zusammenhängen. Der Punkt dient auch als Ersatz-Ort für Gruppierungen oder Strukturen (Schwerpunkt, Mittelpunkt, …).


Kommentar abgeben