AAA 1: Trajektorien und Geschwindigkeiten in Galaxien
Adolphis Astronomie-Abend 1
Bevor wir zu konkreten „Berechnungen im warmen Kämmerlein“ kommen, müssen wir uns noch einmal klar machen, was wir in der Astronomie „wissen“ können:
Welche Bedeutung haben Hypothesen bei der Erkennung der Welt? Ist das Erkennen eines Musters schon eine Hypothese? Welche Muster standen in der Astronomie am Anfang?
Jedes autark bewegliche Lebewesen („Tier“) trifft Entscheidungen auf Grund einer strukturierten Erwartung („Erwartungsbaum“) und greift dabei auf ein Muster zurück, das eine Mischung aus vorgegebenen („Instinkt“, Gene) und erworbenen („Erfahrung“) Handlungen als Reaktion auf Umweltwahrnehmungen darstellt.
(Z.B. Fluchtverhalten von Krähen… im Punkt 3.5.1 dieser Website)
Der Mensch fügt diesem Muster
-eine abstrakte „Draufsicht“ als Über-Muster
und
-den Wunsch nach „Kausalität“
hinzu.
Die menschliche Reaktion hängt zusätzlich von eigenen „Zielen“ ab und kann deshalb individuell sehr unterschiedlich sein:
-Gleichgültigkeit
-Flucht
-Eingriff (z.B. Angriff)
Dabei entsteht dann neue „Erfahrung“ als Grundlage für zukünftiges Handeln!
MENSCHLICH typische Beispiele komplexer Erwartung:
Nonverbale Synchronisierung des inneren Ablaufs mit dem äußeren:
Musik-Hören mit Hilfe des Rhythmus und mit Hilfe des harmonischen Erwartungbaumes (Spannung durch Dissonanz-Konsonanz)
Verbale Synchronisierung des inneren Ablaufs mit dem äußeren:
Sprache hören (i. U. zum Lesen!) mit Hilfe des inhaltlichen Erwartungsbaumes (Spannung durch Rhetorik!)
Beispiel Astronomie:
TIER: Ist an Tag-Nacht-Wechsel gewöhnt und fertig.
MENSCH: Woher kommt das „wirklich“?
(Mensch hat das Bewusstsein von scheinbaren und echten Zusammenhängen UND das Kausalitäts-Bedürfnis!)
(Aber: Auch Tiere sind punktuell neugierig!)
MENSCH:
Erlebt
– Tag-Nacht-Wechsel wie Tiere als zuverlässige Ordnung
– Mondphasen als Ordnung
– Jahreszyklus als Ordnung
Benötigt für landwirtschaftliche Erfolge genaueres Wissen um Jahreszeit (Voraussetzung: Übertragung von Erfahrungen mittels Sprache und Speicher)
– Himmelsscheibe von Nebra
– Steinkreise
Himmel „gibt Zeichen“ für irdischen Erfolg!
MENSCH:
Erlebt neugierig neben Sonne und Mond unterschiedliche Sterne: Fixe und wandelnde
Mit viel Akribie lassen sich Grundmuster der Bewegung aller Planeten ermitteln.
Mit noch mehr Akribie lassen sich Muster der Abweichungen vom Grundmuster ermitteln.
Da keine Einflussmöglichkeit durch den Menschen erkannt wird, ist alles unmittelbar „göttlich“.
Beispiel Mond:
-wandelbare Phase (eigener Rhythmus)
-wandelbare Höhe über dem Horizont (Jahresrhythmus)
Beispiel Wandelsterne:
-Mars: Ringsum-Bewegung vor der Himmelskugel mit rhythmischen Schlaufen
-Venus: Pendelbewegung um die Sonne
Versuch der mechanischen Konstruktion der Bewegung aus Rotationen auf Kreisen („astronomische Uhren“)
Hypothese des heliozentrischen Weltbildes (Antike!)
Erkenntnis, dass man exakte Messungen benötigt, um Hypothesen zu prüfen.
Was ist messbar?
Winkel über Horizont und Winkel zur Nordrichtung
(räumliche Polarkoordinaten auf der Himmelskugel)
Was kann man daraus berechnen?
Keplers Hypothesen:
– Kreise? Nein…
– exzentrische Kreise? Kreis-Überlagerungen? Nein…
– Ellipse mit konstanter Geschwindigkeit? Nein…
– Ellipse mit ganz konkretem Geschwindigkeits-Mittelpunktabstands-Gesetz? Nein…
– Ellipse mit ganz konkretem Geschwindigkeits-Brennpunktabstands-Gesetz!
Wie kam Kepler darauf?
Exakte Messung der relativen Koordinaten durch Tycho Brahe
räumliche Polarkoordinaten auf der Himmelskugel mit Zeit:
Zeit Höhe Azimut
6.4.23 22:34:15 23,5° 44,5°
7.4.23 22:20:45 23,0° 43,0°
Aus diesen lokalen Daten sind die absoluten (Äquatorebene) Winkel-Koordinaten bestimmbar, aber NICHT die Raumkoordinaten einer „Bahn“!
Struktur-Hypothese für gemessene Daten und Rechnungen
Keplers jahrelange Rechnerei: Daten von Tycho Brahe als räumliche Polarkoordinaten zu bestimmten Zeitpunkten
Diese Daten müssen interpretiert werden als
-Projektionen eines beweglichen Objektes aus der Sicht eines bewegten Objektes auf einen festen Hintergrund
-Da beide Bewegungen unbekannt sind, muss man Hypothesen aufstellen, berechnen und mit den bekannten Daten vergleichen
-Als Nebenbedingungen müssen alle bekannten Rhythmen erfüllt werden
-Je 7 geometrische Freiheitsgrade beider Ellipsen müssen iterativ genähert werden:
(3 Ortskoord. MP, gr. u. kl. HA, Neigung gegen Ebene, Drehung um Achse (dynamisch: SP-Brennpunkt))
Keplers Rechen-Ergebnisse als Struktur-Hypothese für allgemeine Planeten-Bewegungen
– absolute Bahnorte von Erde und Mars liegen auf Ellipsen
– Sonne befindet sich in einem Brennpunkt jeder Ellipse (enthält indirekt den Satz der Impulserhaltung)
– Geschwindigkeitsgesetz jeder Ellipse als Flächensatz (enthält direkt den Satz der Drehimpulserhaltung)
– Umlaufzeit-gr. HA-Gesetz (enthält indirekt zweimal Newton: Äquivalenz von träger und schwerer Masse in Trägheits- und Gravitationsgesetz)
Keplers Hypothesen für die Ursache dieser Bewegungs-Muster sind mystischer Art.
Keplers Hypothesen für die Abstandsreihe der Planeten ist ebenfalls esoterisch begründet.
KEPLER hat also die richtigen MUSTER gefunden, nicht aber deren URSACHE angeben können.
Mit Galileis Arbeiten zu
-Fallgesetz (Artillerie, Auftragsforschung)
-Schwingungen (z.B. Musik, zusammen mit seinem Vater)
war der geometrische Gedanke der Zerlegung in Komponenten auf die Physik bewegter Objekte übertragen worden.
Newton konnte mit den physikalischen Ergebnissen von Galilei und den mathematischen von Kepler seinen hypothetischen Gravitationsansatz prüfen. Mit seinem Verständnis der Differential- und Integral-Rechnung war er in der Lage, auf einer höheren Abstraktionsstufe zu arbeiten und die Ergebnisse seiner Vordenker als Spezialfälle unter der Vielfalt der Lösungen zu erkennen.
Was kam nach Newton?
Messung einer endlichen Lichtgeschwindigkeit
-Problem der „Gleichzeitigkeit“ erkannt
-Transformationen in einer „Raum-Zeit“ betreffen auch die Masse
Messung der Rotverschiebung
Unklarheit der Hintergrundstrahlung, Schwarze Löcher
Neue kosmologische Modelle wurden erarbeitet und werden ständig über Kreuz auf Widerspruchsfreiheit überprüft. (Kein Labor…)
ZIEL dieser Vortragsreihe:
Verständnis der rein klassisch-mechanischen WW in Galaxien auf Basis der Newton-Dynamik:
Geschwindigkeits-Profile (heute: AAA 1)
Statistische Ansätze (nächstes Mal, siehe: AAA 2!)
Heute beschränken wir uns also auf
- Kreisbahnen und ihre Geschwindigkeiten
- Wechselwirkung von „Probemassen“ mit diversen stetigen Masseverteilungen
Dazu greifen wir am Anfang auf die in vergangenen Vorträgen (Trajektorien um nicht-kugelsymmetrische Masseverteilungen) dargestellten Kraftfelder zurück und variieren dann die damals als homogen verteilten Massen zu analytisch beschreibbaren Dichteverteilungen. (Ähnlich dort nachlesbar)
Unsere Vorstellungskraft ist im allgemeinen überfordert, wenn wir uns gravitative dynamische Wechselwirkungen ausmalen sollen. Ein einfaches Beispiel soll das demonstrieren:
Es sei eine Kepler-Ellipse gegeben, der Planet befinde sich in der Apoapsis. Hier wird er plötzlich stark beschleunigt, so dass es ihn weit hinausträgt. Wie sieht seine Bahn jetzt aus?
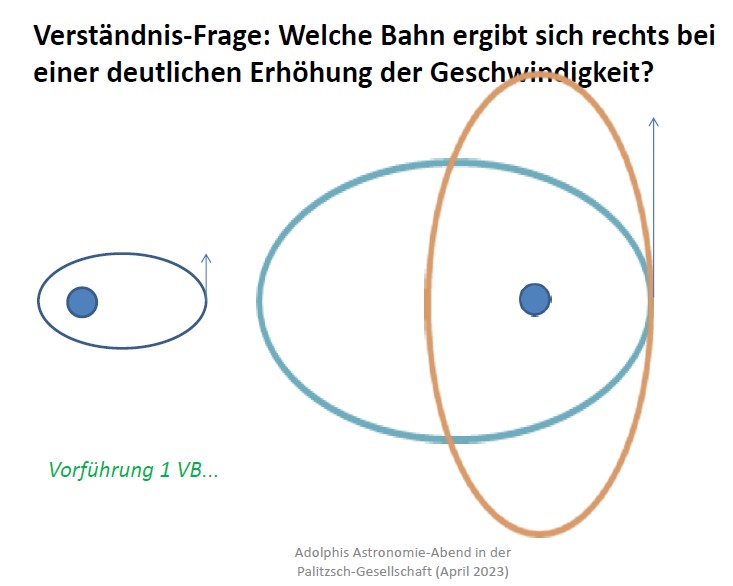
Man ist geneigt, die hellbraune Bahn zu wählen, weil der neue „Schwung“ in diese Richtung zeigt. Richtig ist aber, dass die Apsidenlinie erhalten bleibt, wenn es keine radiale Komponente der Beschleunigung in den Apsiden gibt. Nur in diesen Punkten ist durch den Rechten Winkel des Fahrstrahls räumliche (und also auch zeitliche) Symmetrie bezüglich des Brennpunktes der möglichen Ellipsenschar gegeben. Die hellbraune Ellipse verletzt die Brennpunkteigenschaft der gravitativen Ellipse.
Hieraus folgt, dass man mathematisch sehr genau die Physik umsetzen muss, wenn man „im warmen Kämmerlein“ astrophysikalische „Experimente“ machen will.
FRAGE: Welche Bahn ergibt sich um mehr als eine Masse?
ANTWORT: Auf den ersten Blick chaotische Bahnen, die analytisch nicht beschreibbar sind.
FOLGERUNG: Schrittweise vorgehen:
–BERECHNUNG idealisierter Kreisbahn-Geschwindigkeits-Profile in stetigen Masseverteilungen (heute)
–ABSCHÄTZUNG statistischer Verfahren unter Berücksichtigung diskreter Stern-Stern-Wechselwirkungen (nächstes Mal)
Berechnung der Geschwindigkeits-Profile
Vorgehensweise:
- Kraftprofile von Masseverteilungen berechnen
- Schwere-Trägheits-Äquivalenz für Kreisbahnen einsetzen
- Geschwindigkeitsprofil ableiten
Erinnerung an vergangene Vorträge: Kraftprofile diverser Masseverteilungen
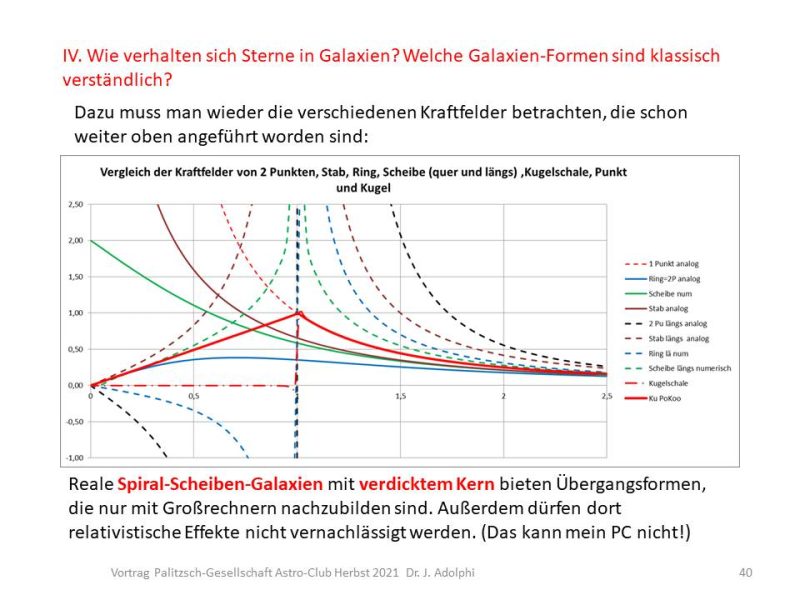
Hier einige Ergebnisse von eigenen Berechnungen der Kreisbahn-Geschwindigkeits-Verläufe über den Radius in Abhängigkeit von der Masseverteilung in Galaxien.
Sie bieten eine knappe Übersicht über den Zusammenhang zwischen Galaxien und ihren Grund-Formen und ihren Geschwindigkeitsverteilungen, die dann beliebig überlagerbar wären (Superpositionsprinzip der Vektorrechnung):
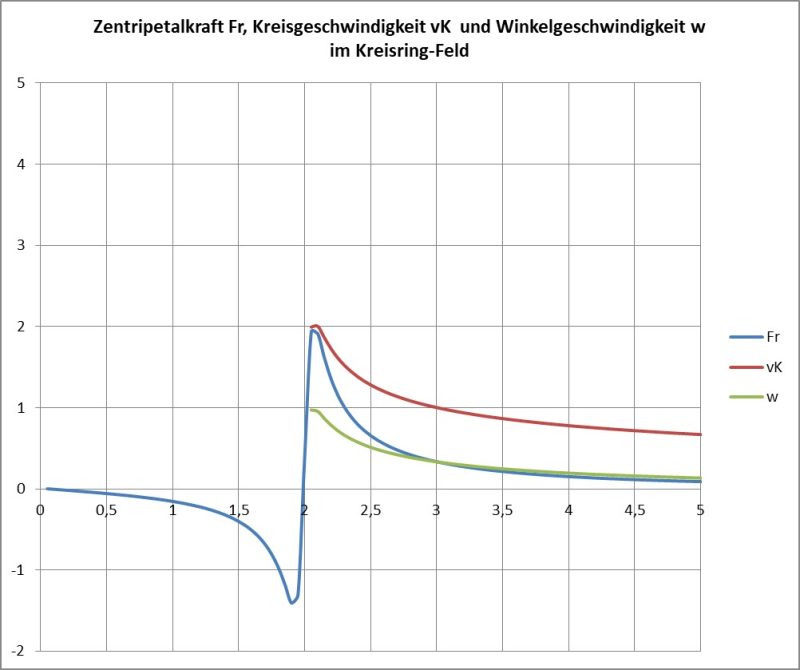
Die Singularität des Ringes weist auf seine strukturelle Instabilität hin, der Richtungswechsel der Kraft allerdings lässt auf statistische Stabilität schließen.

In manchen Publikationen wird aus konstanter Geschwindigkeit auf konstante Kraft geschlossen und daraus „dunkle Materie“ abgeleitet…

Hier ist ein fast fließender Übergang am Kugelrand einer hinreichend großen Kugel (absolut sind alle gleich schwer!) festzustellen, weil die Dichte sehr stark sinkt.

Hochinteressant ist die konstante Winkelgeschwindigkeit aller frei beweglichen Punkte im Inneren!!! (Nicht zu verwechseln mit einer festen Kugel!)

Konstante Kraft über einen weiten Radiusbereich bedeutet NICHT konstante Geschwindigkeit oder konstante Winkelgeschwindigkeit!!!

In der Folge werden nun Rotations-Ellipsoide betrachtet, die einer „typischen“ Galaxie schon näher kommen.





Hier ist eine Form gefunden worden, die schon in „Rein-Form“ (also ohne Superposition) einen großen Bereich konstanter Geschwindigkeit aufweist.


Im homogenen Fall treten die schon bekannten Ähnlichkeiten mit der Kugel (in der Rotationsebene!) auf.



Nun kann man auch noch den Grenzfall einer flachen Scheibe mit diversen Dichtefunktionen betrachten:

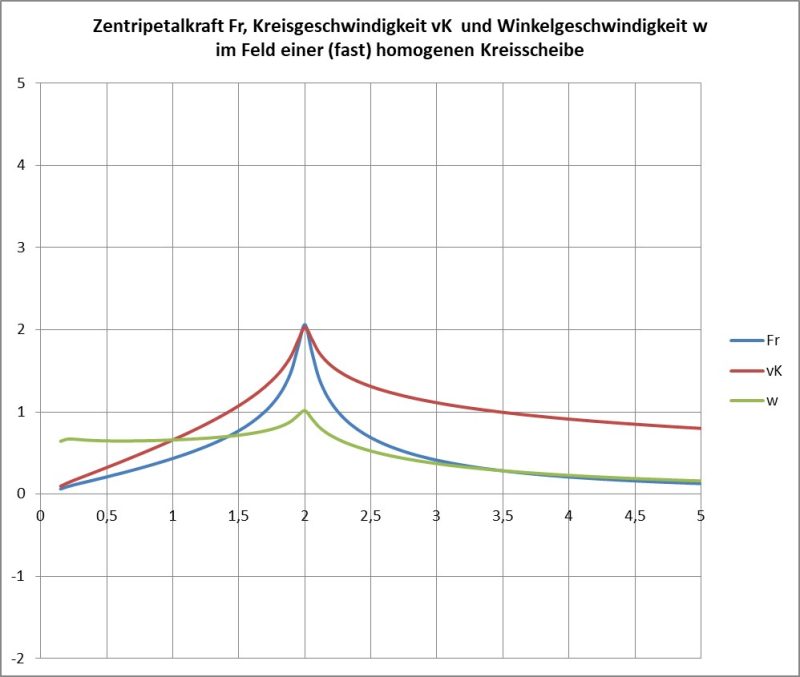

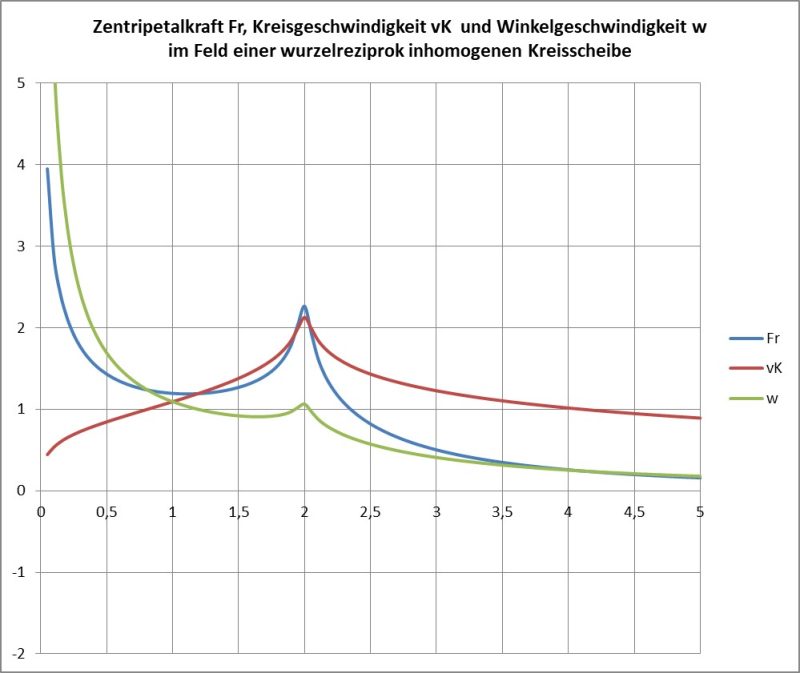
Für den Ring aus diskreten Massen kann man verschiedene Annahmen treffen:
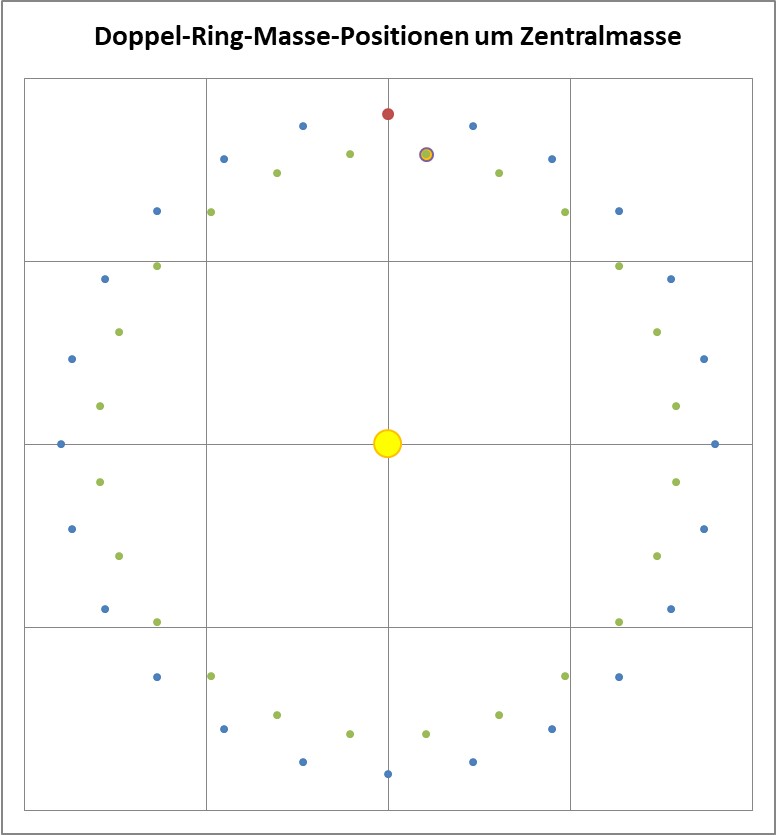


Gruppiert man die Ergebnisse, kann man u.a. folgende Übersichten gewinnen:



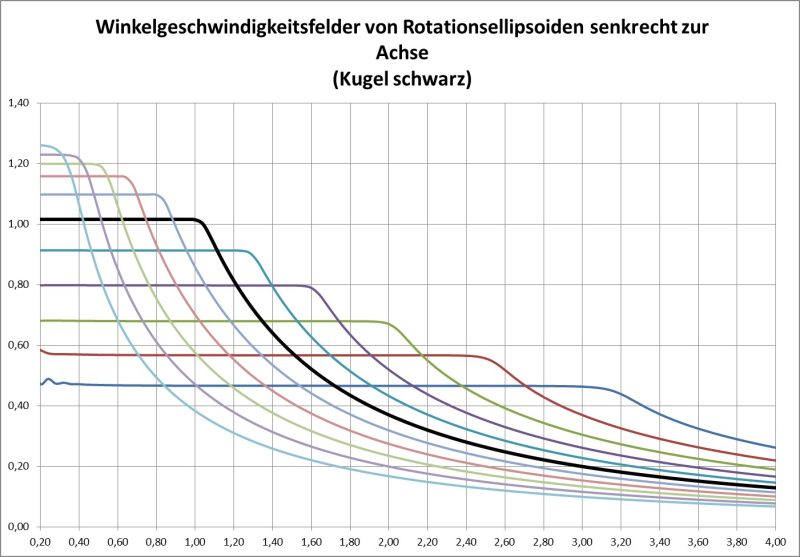

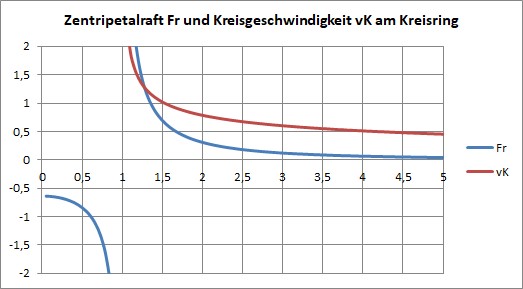


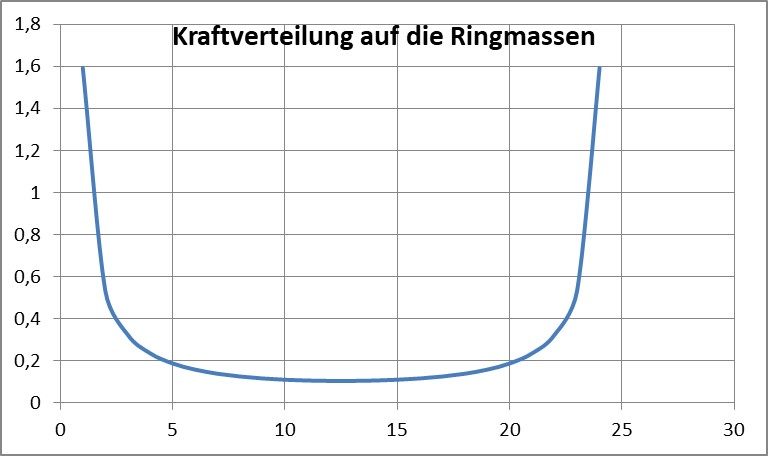


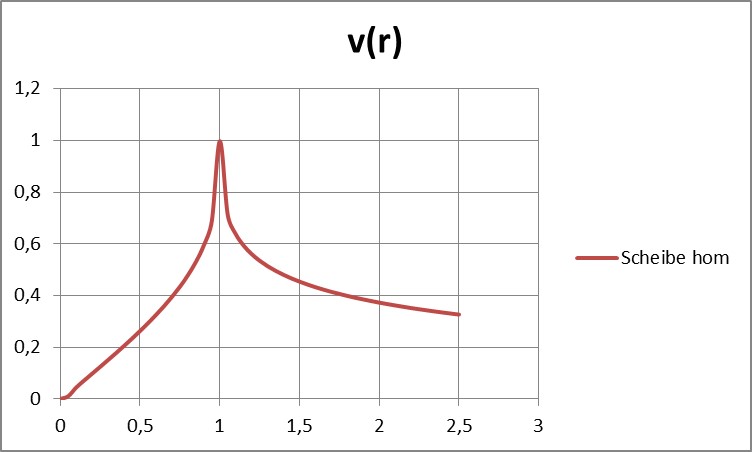

In der Diskussion sollte man besonders beachten, dass es Radius-Bereiche geben kann, in denen die Geschwindigkeit konstant ist, OHNE dass die Kraft konstant ist (was ja physikalisch auch ein Unding wäre, aber in diversen Veröffentlichungen so formuliert worden ist…)
Mit Hilfe der Überlagerungsmöglichkeit ist es also grundsätzlich auch rückwärts möglich, aus jedem erzeugten oder beobachteten Geschwindigkeitsfeld auf eine ursächliche Masseverteilung zu schließen. Kann man entsprechende Massen nicht „sehen“, beginnt das Feld der Spekulation…
Kommentar abgeben