2.4.1.1.2.4 Reiner Schwerkraft-Fall: Ästhetik pur
Zusammenfassend betrachten wir noch einmal Biegung und Stauchung im natürlichsten aller Fälle, nämlich allein durch die Schwerkraft oder eine andere konstante Beschleunigungskraft verursacht, die plötlich einschaltbar sein soll. Dann wird der entspannte Balken oder Stab plötzlich belastet und reagiert elastisch. Diese Reaktion wollen wir unterschiedlich dämpfen und beobachten, was passiert.
Mit den Erfahrungen der vorangegangenen Abschnitte ahnen wir schon, was passiert.
1. Zuerst die ungedämpften Formen
a) Biegeschwingung
Es entsteht eine Schwingung, die ziemlich „harmonisch“ aussieht und auch eine schwache erste Oberfrequenz aufweist, die etwa beim 6,3-fachen der Grundfrequenz liegt (15,5/2,5 in 0,00001Hz), wie in den vorigen Abschnitten schon erarbeitet worden ist. Die einspannungsnahen Schwinger machen eine Trapezform-ähnliche Bewegung.
b) Längsschwingung
Zuerst mehrere Perioden durch eine stärkere Federkonstante und Beschleunigung, um das Spektrum der Massen zu bestimmen, die dicht an der Einspannung liegen, denn deren Bewegung sieht sägezahnförmig aus. Das Spektrum zeigt wirklich die ungeraden (3-, 5-, 7- und schwach 9-fache Grundfrequenz) Oberwellen, die zu erwarten waren.
Hier die zum Vergleich mit den folgenden Diagrammen geeigneteren Paramater-Einstellungen für nur zwei Schwingungen (im Vergleich hängend und stehend):

Hängend
Stehend
In beiden Fällen sind die „Dreieck-Schwingungen“ der nahe der Einspannung liegenden Massen zu sehen, die sich in der Fourier-Analyse als die Wirkung der ungeradzahligen Oberschwingungen erweisen. (Dass die geradzahligen fehlen, liegt an der Einspannung.)
2. Leicht gedämpfte Schwingungen
a) Biegeschwingung
Das „Überschwingen“ ist deutlich geringer geworden und man ahnt schon den Gleichgewichtswert von 12. Die Oberschwingung der oberen Massen ist nur noch schwach zu erkennen.
b) Längsschwingung

Die Dreieckschwingung der oberen Massen ist noch gut zu erkennen.
Beim Vergleich beider Schwingungstypen ist zu beachten, dass im Diagramm der Biegeschwingung der Abstand zwischen den Massen konstant ist und das Schwingungs-Diagramm lediglich die Abweichung jeder Masse von der ursprünglichen Geraden (Horizontalen im Diagramm) anzeigt, während das Strobogramm die jeweils echte Form zu verschiedenen Zeitpunkten darstellt. Das Diagramm der Längsschwingung zeigt die tatsächlichen Orte (und damit ihre zeitlichen Änderungen der Abstände zwischen den Massen) an.
3. Aperiodischer Grenzfall
a) Biegeschwingung
Jetzt ist der Endwert von „Durchbiegung 12“ schnellstmöglich stabil erreicht. Wie nicht anders zu erwarten, ist im ausgeschwungenen Zustand das statische Gleichgewicht dadurch erreicht, dass die Teile in der Nähe der Eispannung ein größeres Biegemoment durch eine größere Krümmung ausgleichen.
b) Längsschwingung
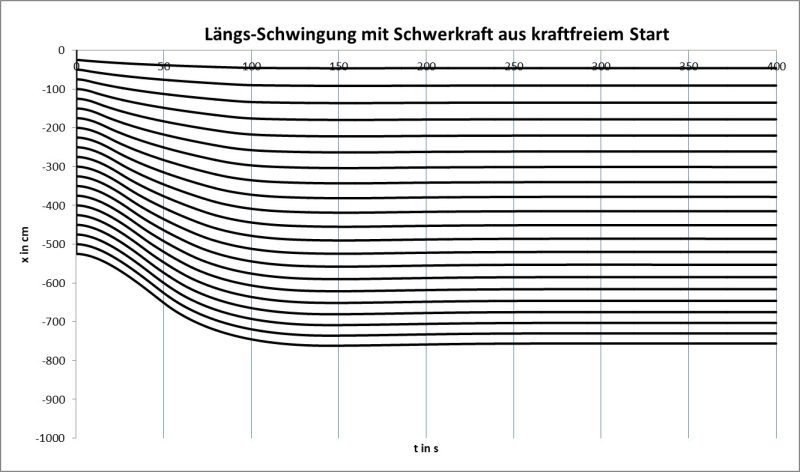
Bei scharfem Hinsehen erkennt man, dass die mittleren Massen keinen „rein fließenden“ Übergang hinkriegen, hier ist ein Rest an Oberwelle zu ahnen.
4. Stärker gedämpfte Schwingung
a) Biegeschwingung
Der Endwert wird erst später erreicht. Das Strobogramm ist auch weniger gespreizt. (Die theoretische Linie zur Prüfung des Modells – Funktion 4. Grades: [y = K * (x^4 – 4*x^3 + 6*x^2)] liegt durch die starke Diskretisierung des Modells, dessen Krümmung quasi erst in der ersten Masse nach der Einspannung beginnt, etwas unter der Modell-Linie.)
b) Längsschwingung

Wie nicht anders zu erwarten, müssen die oberen „Federn“ stärker gedehnt sein als die unteren, weil oben „mehr schwere Masse“ durch die Federkraft ausgeglichen werden muss. Das statische Gleichgewicht ist nun erreicht. Der Rest von „Welle“ ist mit gutem Willen noch zu vermuten… Bei stärkerer Dämpfung ist er dann „weg“.
Die Umkehrung der Beschleunigungskraft würde zu einer Stauchung führen, wie sie bei einer Reihenschaltung von stehenden (statt hängenden wie oben! – man stelle sich das Diagramm auf den Kopf gestellt vor…) Federn und Massen zu erwarten ist:

Einschub: Überschlagsrechnung zur Prüfung des Modell-Ergebnisses:
Alle Funktionen sind offenbar linear, so dass wir mit Mittelwerten leicht rechnen können. (Die unbelasteten Federn ergäben eine Länge von 21*25=525. Stimmt.)
21 Massen der Größe 1 hängen bei einer Beschleunigung von 0,2 an 21 Federn der Länge 25 und der Konstante 0,2. Wie lang ist die Kette dann?
Im Mittel hängen 11 Massen an jeder Feder, welche im Mittel somit um 11*0,2/0,2 Einheiten gedehnt wird, was 21*36 = 756 als Position für die letzte Feder ergibt, was mt dem Diagramm der Dehnung übereinstimmt. Bei der Stauchung wirkt die Kraft in die Gegenrichtung und ergibt eine Kettenlänge von 21*14=294, was ebenfalls übereinstimmt.
Alle diese Bewegungs-Formen haben einen großen ästhetischen Reiz, den wir alle empfinden, ohne ihn alle begründen zu können. Das liegt in unserer animalischen Geschichte als Art begründet, in der wir, wie auch heute noch viele Tiere außer uns, Schwingungen und Ausgleichsprozesse ständig um uns haben und berücksichtigen müssen: Im Winde oder unter unserer Last schwingende Äste, durch unsere Muskeln abzufangende Sprung-Landungen, unsere Trägheit und die der Beutetiere beim Kurvenlauf usw. usf. Überall begegnen uns Bewegungen, die mit Kräften, Trägheit und Elastizität verbunden sind. Im weiteren Sinne gehören z.B. auch Wärme-Übergänge dazu, die aber weniger zu sehen, als vielmehr zu fühlen sind. Wir haben also ein „ganz natürliches“ Verhältnis dazu und können es also als „schön“ oder „ästhetisch“ oder eben auch ganz einfach als „natürlich“ empfinden, was Mathematiker und Physiker durch Differentialgleichungen zu beschreiben gewöhnt sind!
Damit wird dieser Abschnitt über die Schwingungen eines Stabes/Balkens abgeschlossen. Wer weitere Ideen hat, das einmal erfolgreich aufgebaute und getestete Modell auszuschlachten, bitte melden!!












Kommentar abgeben