2.8.3.2 Spiel mit der Kepler-Ellipse
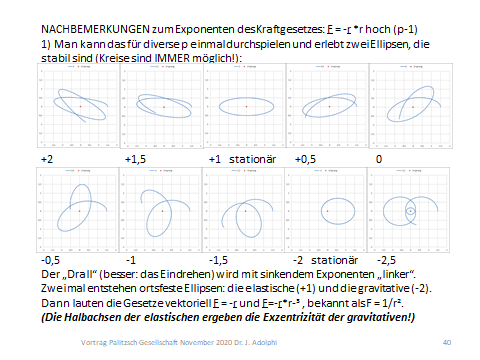
Die Kepler-Ellipse ist (das sei hier vorweggenommen) eine von nur zwei stationären Ellipsen, die bei der Variation des Exponenten eines Kraftfeldes, das NUR vom Abstand abhängt, entstehen:
– elastische Ellipse (Kraftzentrum im Mittelpunkt MP) mit F prop. r (diese physikalische Ellipse hat die volle geometrische Ellipsen-Symmetrie, nämllich zwei senkrecht zueinander stehende Achsen)
– gravitative Ellipse (Kraftzentrum im Brennpunkt BP) mit F prop. 1/r² (diese physikalische Ellipse hat nur eine Symmetrieachse, denn die Kräfte und Geschwindigkeiten sind um beide Brennpunkte verschieden, die Ellipse aber zeitlich in beiden Richtungen durchlaufbar)
(Geht man von Einsteins Hypothese aus, dass „Gott nicht würfelt“, so entsteht die philosophische Frage, nach welchem Prinzip einer der beiden Brennpunkte für die Zentralmasse ausgesucht wird… Die Lösung dieser Frage ist hoch-theoretisch: Versteht man diese Ellipse als perfekte Apsidenliniendrehungs-Überlagerung, erübrigt sich die Frage von selbst.)
Ich habe diese Variation einmal durchgespielt, wozu ein kleines VBA-Programm reicht, welches eine EXCEL-Tabelle zum Zwecke der Diagramm-Erstellung füllt. Die Zeit habe ich in 100.000 Abschnitte geteilt, um die Fehler der numerischen Integration zu minimieren, gebe aber nur jeden 100. Punkt an EXCEL weiter. 1.000 Punkte reichen für ein hinreichend „glattes“ Bild im Diagramm, auch wenn man mehrere Perioden überstreicht, um die Stationarität zu veranschaulichen.
Damit die unterschiedlichen Kraft-Felder und ihre Wirkungen gut nachvollziehbar sind, wird neben den Bahn-Plots und den Bahnparametern (kartesische Koordinaten x und y, Zentralabstand, Geschwindigkeitsbetrag, Krümmung und Drehimpulsbetrag auch das dazugehörige Potential (quasi als die Symmetrieachse enthaltenden „Schnitt“ durch den Potential-„Topf“) ausgegeben.
Man muss sich etwas einlesen, aber dann hat man viel Spaß. Bei den Bahn-Plots und den Potentialen sind alle drei Varianten (Gravitation (1), Elastik (2) und freier Exponent (3)) übereinander gelegt, bei den Parametern sind die Diagramme einzeln angelegt, um die Übersicht nicht zu verlieren.
Interessant ist besonders die Gegend um den Exponenten -2 herum, also die Gegend der geringen Abweichungen vom Gravitationsgesetz:
Hier noch ein Pärchen von rückwärts und vorwärts drehenden Rosetten, die vorwärts drehende dabei mit neuer, fast stationär eingestellter Figur:
Die wichtigste Erkenntnis ist, dass die beiden unterschiedlich ausgeformten Krümmungsmaxima nur bei der gravitativen Ellipse F prop. r hoch-2 gleich hoch sind (bei der elastischen ist das trivial ebenso). Nur bei diesem Exponenten gleichen sich die veränderten Anziehungskräfte und Winkelgeschwindigkeiten aus. Der Drehimpuls ist bei allen hier aufgezeigten Beispielen im Startpunkt identisch und über die Zeit konstant.
Zwei Nachbemerkungen:
Erstens: Selbstverständlich sind für alle rotationssymmetrischen Felder Anfangsbedingungen einstellbar, für welche sich eine Kreisbahn ergibt – bei dieser ist naturgemäß keinerlei Apsidendrehung erkennbar!
Zweitens: Selbstverständlich kann man nur dann von einer allgemein stationären Ellipse sprechen, wenn diese nicht nur für einen einzigen, sondern für alle Parametersätze gebundener Zustände stationär ist! (Das muss man also hinreichend durchspielen! Einen dritten Exponenten dafür habe ich noch nicht gefunden…)
Drittens: Eine systematische Veränderung des hypothetischen Kraft-Exponenten ergibt das folgende, eine Gesetzmäßigkeit offenbarende Bild (die Vergleichs-Potentiale zur Besseren Vergleichbarkeit der Entwicklung der Formen einfach einmal weggelassen):
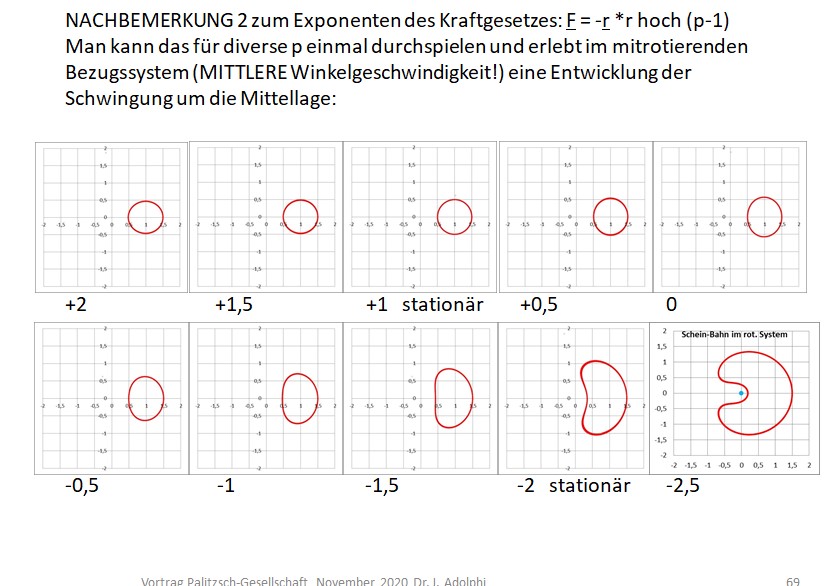
Die Winkelgeschwindigkeit des mitrotierenden Systems wurde jeweils einer Abstands-Periode angepasst, was nur im stationären Fall -2 im festen Bezugssystem einem Winkel von 360° entspricht! Im Fall +1 entspräche das nur 180°.
Erstaunlich ist bei dieser Anpassung der Winkelgeschwindigkeit, dass diese nicht so sehr schwankt, wie man vermutet. Das hängt allerdings von den Anfangsbedingungen (Ort und Geschwindigkeit) der Probemasse ab. Hier der Plot für die oben verwendeten Daten:
Das kosmologisch wirklich Interessante an dieser gesamten Betrachtung ist der Umstand, dass man für einen gegebenen Abstand von einer nicht-sphärischen Zentral-Masse-Verteilung einen „hypothetischen Ersatz-Exponenten“ für das Gravitationsgesetz bezüglich einer zentralen Punktmasse finden kann, der die gleiche Rosette ergibt wie die „wirkliche“ Masseverteilung beim Standard-Exponenten -2. (s. oben Punkt 2.8.1) Dass dieser hypothetische Exponent auch noch Abstands-abhängig ist, macht „das Kraut richtig fett“!
Fragt man sich weiterhin, ob es auch andere „stationäre Bahnen“ bei anderen Kraftfeld-Exponenten geben kann, so lautet die eingeschränkte Antwort „ja“: Es gibt sie für angepasste Drehimpuls-Werte. Hier (in Fortführung der obigen Übersicht) einige Beispiele:
Die Symmetrie wechselt zwischen 1-achsig und 2-achsig. Im dritten Fall ist der Drehimpuls etwas erhöht worden, um Numerik-Artefakte in der Nähe des Zentrums auszuschließen.
(Vergleich mit Quanten-Zuständen in Elektronenhüllen nicht abwegig: „Eigenfunktionen“.)




















Kommentar abgeben