Energie-Satz
Kann man verstehen, warum der Energie-Satz schlechthin als Kernsatz der Physik gilt? Es gibt doch auch viele andere Erhaltungs-Sätze!
Das Besondere ist, dass mit ihm die unterschiedlichsten Energie-Formen in Zusammenhang gebracht werden können, dass die „Energie-Umwandlng“ einfach formulierbar wird und die Vorstellung vom „Verschwinden“ oder vom „Erzeugen“ von Energie als oberflächlich entlarvt wird.
Aber schon bei einfachen Fragen zu den mechanischen Energieformen der kinetischen und potentiellen Energie taucht das Problem des Bezugs auf: Das weist darauf hin, dass wir es entweder mit einer intervallskalierten Teil-Größe zu tun haben wollen oder den „Welt-Formel-Ansatz“ nicht zu Rate ziehen wollen.
Die Lösung ist, dass wir immer das System angeben müssen, in welchem wir die Energie betrachten, und dass wir unterscheiden, ob es abgschlossen ist oder nicht.
Und selbst da gibt es Größen, die viel anschaulicher sind. Nehmen wir die Mechanik: Da ist es der Impuls. Er ist anschaulicher als die kinetische Energie, weil er zwei unmittelbar einsichtige Proportionalitäten enthält:
- Impuls proportional zur Masse (verhältnisskaliert: Masse Null ist absolut)
- Impuls proportional zur Geschwindigkeit (intervallskaliert: Bezugssystem)
also: Impuls ist Masse mal Geschwindigkeit: p = m*v
(p: Impuls im Bezugssystem, m:Masse, v: Geschwindigkeit im Bezugssystem)
Der Impuls ist jedem Tier als „Schwung“ oder „Wucht“ körperlich erfahrbar und also eine unmittelbar in der Vorstellung verhaftete Größe. („Der ist leichter als ich, den renne ich um!“, „Der ist genauso schwer wie ich, da muss ich schneller anrennen als der!“)
Auch die potentielle Energie auf der Erdoberfläche ist in unserem Erfahrungsbereich dreifach (intervallskaliert: Bezugssystem) proportional:
- Wpot = m*g*h
(g: Erdbeschleunigung im Betrag und Richtung konstant, h: Höhe im Bezugssystem parallel zu g)
Die potentielle Energie ist den meisten Land-Tieren als „Kletter-Aufwand“ oder als „Sturz-Folge“ körperlich erfahrbar.
Die kinetische Energie einer bewegten Masse ist NICHT unmittelbar als quadratisch von der Geschwindigkeit abhängig erlebbar. Eher sogar ist das allgemein logarithmisch angelegte Empfindungssystem unserer Sensoren kontraproduktiv. Wir wissen zwar, dass es mehr weh tut, aus großer Höhe herabzufallen als aus kleiner, dass es mehr weh tut, mit großer Geschwindigkeit gegen eine Wand zu rennen als mit kleiner, aber wir ordnen das nicht einer bestimmten Potenz der Geschwindigkeit im entsprechenden Zusammenhang zu.
Eine einfache Probe unserer unsicheren Vorstellungskraft von kinetischer Energie möge das verdeutlichen:
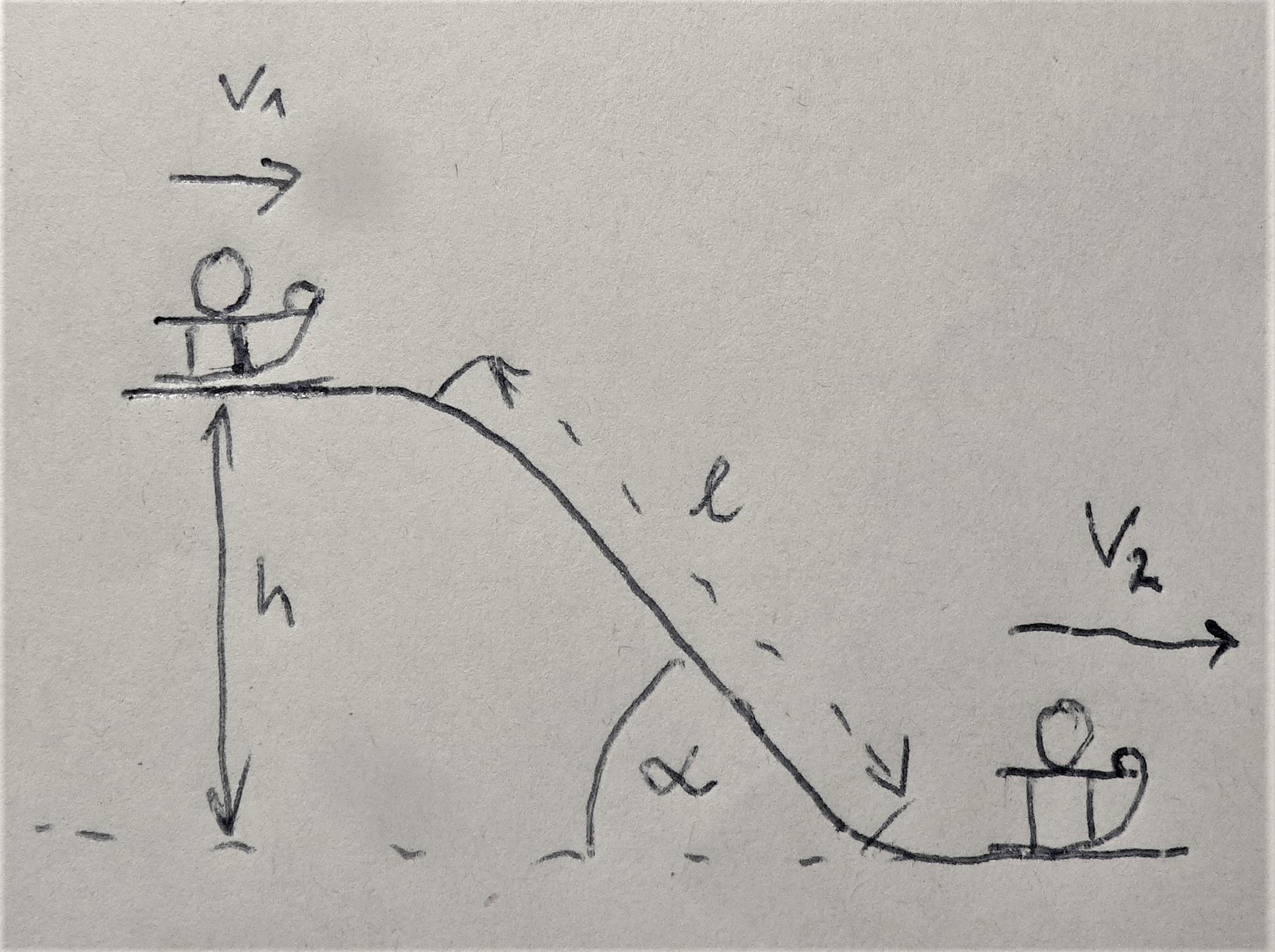
Zwei gleich schwere Kinder rodeln mit gleichen Schlitten („Bauchklatscher“) am gleichen Hang. Kind A startet aus der Ruhe, Kind B mit Anlauf. Kind A kommt unten mit 18 km/h an, Kind B mit 22 km/h. Wie schnell war die Anlaufgeschwindigkeit von Kind B?
Aus dem Gefühl für den Energiesatz schließen wir: 4 km/h (Addition als Berechnungs-Grundlage wegen einer Additivität im Erhaltungssatz).
Nun, wir ahnen es bereits: Das Ergebis ist falsch, selbst wenn wir alle Reibung in Luft und auf dem Schnee vernachlässigen.
Warum ist das falsch?
1. Gedankengang: anschaulich mit einfacher Proportionalität
Der langsame A konnte die Hangabtriebskraft viel länger auf sich wirken lassen als der schnelle B. Er hat also einen größeren Impuls durch das Bergabfahren erhalten können als B. Das heißt im Umkehrschluss, dass die Startgeschwindigkeit von B größer als 4 km/h gewesen sein muss.
Der physikalische Zusammenhang
Kraftstoß = Impuls (F*dt=m*dv)
mit
F = m*g*sin(alpha) als Hangabtriebskraft
zeigt, dass bei unterschiedlichem dt auch das dv unterschiedlich sein muss.
2. Gedankengang: abstrakt mit Energie-Formeln
Der für beide gleiche Energiegewinn aus der potentiellen Energie der gleichen Höhendifferenz führt wegen der quadratischen Abhängigkeit der kinetischen Energie von der Geschwindigkeit zum Erfordernis des Wurzelziehens aus der Summe beider Energieanteile. Der Zuwachs der Endgeschwindigkeit durch die Startgeschwindigkeit fällt also kleiner als die Startgeschwindigkeit selbst aus. Das heißt im Umkehrschluss, dass die Startgeschwindigkeit von B größer als 4 km/h gewesen sein muss.
3. Rechnerische lösung
Kind A kommt mit 5 m/s = 18 km/h unten an.
Das ist eine kinetische Energie von 12,5 m²/s² * Masse, die einer vorherigen potentiellen Energie von 1,25 m * Masse * 10 m/s² entspricht.
Kind B kommt mit 6,11 m/s = 22 km/h unten an.
Das ist eine kinetische Energie von 18,67 m²/s² * Masse, also 6,17 m²/s² * Masse mehr als Kind A. Dieser Überschuss stammt vom Anlauf, der also eine Geschwindigkeit von der Wurzel aus 2*6,17 m²/s² gehabt haben muss:
3,51 m/s = 12,65 km/h
Kind B ist also dreimal so schnell gestartet, wie wir vermutet haben. Das ist eigentlich ziemlich schlimm, wie wir hier von unserem Gefühl irregeleitet werden! (Siehe auch „Lernen und Verstehen„)
Da entsteht doch gleich eine heuristische Frage:
Kann man auf dieses Ergebnis auch kommen, wenn man vom Impuls, der „erfühlbaren Größe“, ausgeht?
Antwort: JA!
Wir müssen uns nur fragen, wie sich ein Impuls ändert, wenn eine Kraft wirkt, wie in unserem obigen Beispiel die Hangabtriebskraft. Eine Änderung beschreiben wir hier mit einem kleinen „d“ (Differenz) und setzen ohne Widerspruch zur „fühlbaren“ Erfahrung:
m*dv = m*(v2-v1) = F*dt = F*(t2-t1)
„Ein Kraftstoß (Kraftwirkung im Zeitintervall dt) bringt eine Impulsänderung (Geschwindigkeitserhöhung dv einer Masse).“
In unserem Fall kommt die Kraft als Komponente der Schwerkraft parallel zum Hang mit dem Winkel alpha als Hangabtriebkraft zur Wirkung:
Fh = m*g*sin(alpha)
Die Zeit, die diese Kraft wirken kann, ergibt sich aus der mittleren Geschwindigkeit vm und der Länge l des Hangs:
dt = l/vm
Die mittlere Geschwindigkeit ist die Mitte zwischen Startgeschwindigkeit v1 und Endgeschwindigkeit v2:
vm = (v1+v2)/2
Jetzt können wir die Impuls-Entwicklung durch Einsetzen so schreiben:
p2 = m*v2 = p1 + F*dt = m*v1 + m*g*sin(alpha)*l/((v1+v2)/2)
Die Gleichung kann mit (v1+v2) multipliziert werden:
m*v2² + m*v1*v2 = m*v1² + m*v1*v2 + 2*m*l*g*sin(alpha)
Mit der Hanghöhe h = l*sin(alpha) wird daraus:
m/2 * v2² = m/2 * v1² + m*g*h
oder (durch Vergleich mit unserem Schul-Wissen!)
Wkin2 = Wkin1 + Wpot
der Energie-Satz!
(Für Eingeweihte ist die kinetische Energie „das Geschwindigkeits-Integral des Impulses“.)
(UND: Die Masse kürzt sich raus, weshalb die Forderung, dass beide Kinder A und B gleich schwer sein sollen, überflüssig wird, solange keine Reibungen auftrteten.)
Die wichtigsten Umformungen der Energie, die uns im Alltag begenen, sind von den Gesetzgebern durch Festlegung der Maßeinheiten so berücksichtigt worden, dass die Umrechnung trivial ist:
1 Nm = 1 Ws = 1 J
(NewtonMeter = WattSekunde = Joule)
(mechanische = elektrische = kalorische Energie)
Mit dieser Gleichsetzung könnten wir nun berechnen, welche elektrische Energie die Rodel-Kinder beim Bremsen mit einer Dynamo-Maschine „erzeugen und in der Schlitten-Beleuchtung verbrauchen“ könnten oder wieviel Wasser sie in ihrem Rucksack um wieviel Kelvin erwärmen könnten.
Potentielle Energie gibt es in allen Kraftfeldern:
gravitativ, elastisch, elektrisch, magnetisch, …
Potentielle Energie kann auch indirekt über Bindungsenergie in der Thermodynamik oder Teilchenphysik sehr vielfältig verwendet werden.
Somit ist mit der Energie wirklich ein zwar nicht sehr anschaulicher, dafür aber sehr leistungsfähiger Begriff bzw. eine tragfähige physikalische Größe gefunden worden.
Wer das hochintelligent vertiefen will, studiere den Lagrange-Formalismus für die Bestimmung der Bewegungsgleichungen (schließlich befinden wir uns hier auf einer „Struktur“-Seite!!) unter:
https://de.wikipedia.org/wiki/Lagrange-Formalismus
Kommentar abgeben