2.4.1.1.2.3 Biegeschwingung eines inhomogenen Balkens
Kann man das Verhalten eines Anblas-Blättchens eines Holz-Blasinstrumentes mit dem gleichen Modell untersuchen?
Zu diesem Zweck lassen wir einmal testweise die Biegesteifigkeit des einseitig eingespannten „Balkens“ (in der Statik heißt er „Kragbalken“) linear zum freien Ende hin abnehmen. Man kennt ja den Ton eines vom Instrument abgelösten Mundstücks und weiß, dass er unangenehm schrill ist…
Das „Mess-Ergebnis“ mit unserem Modell ist demenstsprechend (Start mit Biegelinie des homogenen Balkens):
Die äußeren Massen zum Rand des Blättchens hin flattern gewaltig…
Die vielen Zwischenwerte habe ich hier nicht dokumentiert, aber wie zu erwarten steigt die Frequenz des ohne Instrument schwingenden Blättchens mit seiner Härte, während die Schwingungsform unverändert bleibt und eine kleine Hoffnung auf Obertöne zulässt. (Aus numerischen Gründen ist der Zeittakt für größere Härte verkürzt worden, die Diagramm-Einstellung aus Vergleichsgründen aber beibehalten worden.)
Das ist natürlich gut so, denn durch die Rückkopplung mit dem Instrument schwingt es beim Spielen teilweise erzwungen mit und stört die eigenen Obertöne des Instruments nicht durch die seinigen.
Hier der ermittelte Zusammenhang zwischen Härte und Eigenfrequenz:

Auf der Abszisse ist eine nicht normierte Härte angegeben, die Frequenz ist auf den Wert der „Härte 10“ normiert. Beim Spielen eines Holz-Blasinstruments bemerkt man, dass man wesentlich tiefere Töne als die des Mundstücks spielen kann (das Instrument ist ja auch viel länger!). Die gewählte Härte das Blättchens ist dann vom Bläser und vom Charakter der Musik abhängig…
Ein „echt konisch“ geformtes Blättchen aber hat einen anderen Verlauf der Biegesteifigkeit, weil das Flächenträgheitsmoment von der dritten Potenz der Dicke abhängt und die zu bewegende Masse von der ersten. (Das Integral über die freie Restmasse ist quadratisch von der freien Länge abhängig – es wird also etwas komplizierter.) Die lokale Biegsteifigkeit ist dann also eine quadratische Form der Länge.
Die so ermittelten Frequenz-Werte weichen naturgemäß von den obigen ab. Sie sind an der „Wurzel“ beim Vergleich einer konischen Zunge mit einem Balken gleicher Gesamtmasse in ihrem inneren Verhältnis, am Ende der Zunge aber vor allem in der Intensitätsverteilung völlig anders.
Zuerst muss aber über eine sinnvolle Anregung des Blättchens gesprochen werden. Die Biegelinie eines homogenen Balkens hat sich nicht als sinnvoll erwiesen, ebenso nicht eine „verschobene“ quadratische Funktion (also eine mit Linearterm). Am besten erweist sich eine rein quadratische Form, die dann in der Schwingung auch gut reproduziert wird, ohne ganz auf Oberwellen verzichten zu müssen. Das Spektrum ist am klarsten dircht an der Wurzel und weist eine Besonderheit bei der vorletzten diskretisierten Masse auf, wie wir gleich sehen werden.
(Die Untersuchungen sind sehr zeitaufwändig, um für jeden Schwinger 1.000 Frequenzen über 40.000 Stützstellen laufen zu lassen, also 40.000.000 Rechnungen für ein einziges Spektrum… Das dauert länger als die Berechnung von je 40.000 Positionen für z.B. 29 Schwinger. Für noch mehr Schwinger bräuchte man nochmehr Zeittakte, um mehr als eine Periode abbiden zu können. Größere Biege-Steifigkeit beschleunigt zwar die Schwingung, lässt die Numerik aber eher aufschwingen, das hebt sich also auf. Deshal sind allein Frequenzverhältnisse interessant und nicht die reinen Frequenzen…)
Das „Flattern“ des Blättchenrandes, das wir oben bemerkt haben, ist jetzt verschwunden und weist nur noch eine Spiegelung am fast glatten Schwingen der vorletzten Teilmasse auf:

29-Massen-Zunge im Schwingungsbild (dem des homogenen Stabes mit schwerer Endmasse sehr ähnlich, bis auf die äußere Masse selbst!)

Start (gestrichelt wie immer) mit einer (flachen!!) Parabelform, wie immer stark überhöht dargestellt.
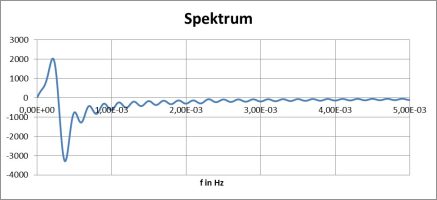
Die Spektren der einzelnen Massen sind interessant (hier am Beispiel einer 21-m-Zunge):
Man erkennt, dass die inneren Massen ein klares Obertonspektrum haben, die äußeren nicht. Daraus zu schließen, man könne diese Töne hören (oder sie trügen wesentlich zur Klangfarbe bei), wäre ein Trugschluss, denn erstens liegt der erste Oberton um einen Frequenzfaktor von über 20 darüber (also mehr als 4 Oktaven!), und zweitens sind die Amplituden ganz innen zu klein gegen die Grundschwingung außen, um wesentlich zum Energiehaushalt beitragen zu können. (Das wäre übrigens einer gesonderten Betrachtung wert!)
Das Obertonspektrum ist etwa so aufgebaut und ändert sich im Bereich zwischen einer Diskretisierung in 11 bis 29 Massen nur unwesentlich):
| f/f2 | f/f1 |
| 1,00 | |
| 1,00 | 20,79 |
| 3,17 | 65,86 |
| 6,73 | 139,86 |
| 8,93 | 185,74 |
| 11,53 | 239,76 |
| 16,80 | 349,28 |
| 23,17 | 481,74 |
| 30,85 | 641,58 |
Die reichlich 20-fache Frequenz ist in den oben angeführten Schwingungsbildern gut als Wellenform innerhalb der schönen Halbwellen zu erkennen. Die höheren Frequenzen sind nur Gezappel, erinnern in ihren Relativwerten aber verrückterweise an den symmetrisch schwingenden homogenen Balken, frei oder beidseitig eingespannt (Deshalb ist auch zusätzlich der relative Wert zur zweiten Frequenz angegeben!). Die Grundfrequenz ist weniger gut aus dem Spektrum abzulesen, dafür aber die Schwingzeit gut aus dem Schwingungsbild.
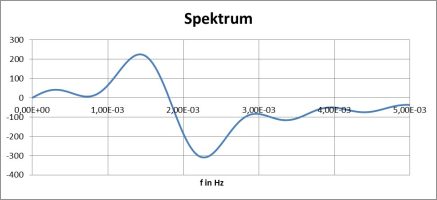
Das gestreckte Spektrum sieht dann so aus:

gestreckte Abszisse für Masse 4
Ein interessanter Fall ist übrigens der Übergang vom stabilen Schwingen zur numerischen Instabilität:
Hier schwingen die inneren Massen direkt gegeneinander. Die Grundschwingung ist fast nicht zu erkennen, aber wenn man die Abszisse staucht, erscheinen erst die sehr schwachen und aber „verschmierten“ Grundschwingungen und dann die ganz hohen „Molekülschwingungen“:


Daraus ergibt sich sofort die Frage, ob das schon alles sei? Also weiter stauchen:

Und siehe da, wir haben wieder etwas über den Übergang von physikalischen und numerischen Effekten beim Modellieren gelernt: Diese fast harmonisch aussehende Obertonreihe (0,26 + n*0,5)Hz ist reiner Fake oder „Artefakt“. Das müsste auch in einem stark gespreizten Schwingungsbild zu sehen sein:

Und tatsächlich: Bei 50-facher Spreizung erkennt man den Beginn des numerischen Aufschwingens nach 700s mit etwa 1/164 Hz, was aber noch nicht zu Chaos führt, sondern die Frequenz langsam steigen lässt. Das sieht dann so aus:

Hier erkennt man schon das langsame steigen der numerischen „Grundfrequenz“.
Und das numerische Chaos? Das ist lustig, wenn man es langsam beginnen lässt, knapp über den metastabilen Werten, hat aber keinerlei physikalischen Sinn:
Zusammenfassung:
Man kann mit etwas Mühe auch einen inhomogenen Stab (hier u.a. ein Blättchen mit rechteckigem Querschnitt, dessen Höhe linear bis zum Ende auf Null abnimmt) modellieren, um seine Schwingungseigenschaften am Modell zu „messen“. Man sollte aber auch ermitteln, wo die numerischen Grenzen des Modells liegen, um keinen Trugschlüssen zu unterliegen.
Ein solches Blättchen zeigt sehr interessante Eigenschaften, die seit den ersten abendländischen physikalischen Experimenten zur Schwingungslehre der Musikinstrumente von Galileo Galilei vor 400 Jahren (ich halte das für die größere Leistung als die astronomischen Beobachtungen, obwohl letztere viel mehr am Weltbild gerüttelt haben als die Verbesserung der Saiteninstrumente das konnte…) immer wieder Liebhaber herausfordern.















Kommentar abgeben