2.8.1.0 Vergleich der nichtstationären Ellipsen von Rotationsellipsoiden und veränderten Kraftgesetzen
Im Abschnitt 2.8.1 wurde der gedankliche Original-Einstieg in das Spiel mit nichtstationären Ellipsen (Rosetten) dargelegt. Hier sollen systematische Vergleiche zwischen den geometrisch ähnlichen Erscheinungen der Rosetten um Rotationsellipsoide (in der Ebene senkrecht zu ihrer Achse) und um Punktmassen bei verändertem Kraftexponenten folgen.
Kann man verstehen, warum beide so ähnlich sind? Und worin bestehen die kleinen Unterschiede?
Zuerst die Fakten für übersichtliche Beispiele, später dann die Überlagerung beider Effekte zum Zwecke ihrer Auslöschung. Dabei sollen aus Vergleichsgründen Parameter verwendet werden, die eine ähnliche geometrische Konsequenz haben.
1. Vorbetrachtung
Grundsätzlich gibt es zu jeder rotationssymmetrischen Situation in einem Feld mit beliebigem Zentral-Abstands-Exponenten einen bestimmten Vektor der Bahngeschwindigkeit zu jedem Zentralabstand, der exakt zur Gleichheit von Anziehungskraft und Trägheitskraft führt, also eine Kreisbahn ergibt.
Das gilt also auch, wie man an den fünf obigen Beispielen sieht, für ein Schwerefeld um ein Rotationsellipsoid, wenn die Bahnebene senkrecht zur Rotationsachse des Ellipsoids liegt. (Die jeweilige Startgeschwindigkeit senkrecht zum vorgegebenen Zentralabstand 2,0 wurde iterativ „erspielt“.)
Jedes andere Paar von Abstand und Geschwindigkeit führt zu einer Schwingung um den passenden Abstand und um die passende Geschwindigkeit, wobei sich ein Austausch zwischen potentieller und kinetischer Energie abspielt.
Die sich ergebende Trajektorie ist im allgemeinen Fall eine Rosette und nur im speziellen Fall von Kugelsymmetrie eine Ellipse.
2. Rotationsellipsoide
Die Anziehungskraft eines flachen Rotationsellipsoids ist in seiner Symmetrieebene größer als die einer Kugel gleicher Masse. Es ergibt sich eine „vorwärts“ präzedierende Ellipse, hier bei 130 % des Durchmessers einer Kugel gleicher Masse. Das VSZ liegt aus der Sicht der umlaufenden Masse „vor“ dem Schwerpunkt der Zentralmasse:
Bei einem schlanken Rotationsellipsoid (80 % Durchmesser) ist die Anziehungskraft kleiner, es ergibt sich eine „rückwärts“ präzedierende Ellipse. Das VSZ liegt aus der Sicht der umlaufenden Masse „hinter“ dem Schwerpunkt der Zentralmasse:
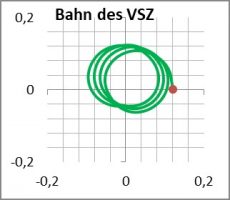
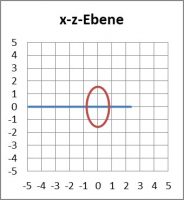
Zur besseren Verständlichkeit sind jeweils vier Bilder angeführt: Die Bahn in der Symmetrieebene xy und senkrecht dazu in xz, die Schein-Bahn in einem konstant mitrotierenden Bezugssystem und die Bahn des „Virtuellen Schwerezentrums“, welches den Ort angibt, an dem sich eine Punktmasse gleicher Kraftwirkung befinden müsste.
3. Kraftfelder abweichender Abstands-Exponenten
Abweichende Exponenten des Kraftgesetzes (rein hypothetisch!) ergeben schon für die Kugel (oder adäquat für die Punktmasse) ähnliche Bilder. Für den Exponenten -1,8 ergibt sich eine Rückwärts-Drehung der Apsidenlinie:
Für den Exponenten -2,1 ergibt sich eine Vorwärts-Drehung:
(VSZ und Schwerpunkt fallen bei der Kugel zusammen.)
Aus diesere Erekenntnis ergibt sich die spannende Frage, ob sich beide Effekte etwa aufhaben können?
4. Trajektorien um Rotationsellipsoide bei abweichenden Kraftfeldern
Tatsächlich lassen sich Paare von Exponenten und Abplattungen finden, die sich aufheben. Hier zwei Beispiele, zuerst der schlanke Fall (80%) mit Exponent -2,1:
Hier der abgeplattete Fall (130%) mit Exponent -1,9:
In beiden Fällen ist eine ortsfeste Ellipse entstanden, deren Schwingungsbilder im mitrotierenden System (nierenförmige Schein-Bahn durch die Coriolis-Kraft!!) auf die Stabilität des Systems hinweisen.
(Der rote Startpunkt bei der grünen VSZ-Bahn zeigt gut an, ob das VSZ „vor“ oder „hinter“ dem Schwerpunkt des Ellipsoids liegt!)
(Bei allen hier behandelten Fällen sind etwa drei Umrundungen durchlaufen worden, um eine gute Vergleichbarkeit zu erzielen.)























Kommentar abgeben