3.1 Anordnungs-„Strukturen“ bei Pflanzen und niederen Tieren
Kann man das Prinzip erkennen, nach welchem sich Sonnenblumenkerne, Muschelschalenflecken oder pflanzliche Individuen untereinander oder mit fremden anordnen?
Wenn wir einmal von einfachen Minimal-Prinzipen wie der Anordnung „auf Lücke“ absehen, die einer Energie-Minimierung gleich kommen, finden wir in der Natur trotzdem fantastisch anmutende „Muster“, die an strukturelle Ursachen denken lassen. Auch der manchmal vorkommende „Goldene Schnitt“ ist noch rein physikalisch-geometrisch zu erklären, wie zum Beispiel als Winkelteilung der Sonnenbumen-Kern-Anordnung oder der Stacheln eines Kaktus (hier in EXCEL in Polarkoordinaten beispielhaft berechnet mit r = Wurzel(n) und phi = n*137,5031° {„Goldener Winkel“} für n= 1 bis 1000, was eigentlich eine radial zwar sehr enge, azimutal aber sehr weit diskretisierte Spirale ergibt, die unübersichtlich wäre, wenn sie nicht intern eine Überstruktur mehrerer anderer „steilerer“ Spiralen enthielte, sofern man die Teilung mit Fibunacci-Zahlen angeht):
Mit markierten Kernen (wenn auch hier nach Fibonacci-Zahlen abgezählt!) kann man Spiralen finden, auch bei den Kakteen:
Bilder-Quelle: Jürgen Meier, Hamburg: http://www.3d-meier.de/tut22/Sonne/Seite1.html; http://www.3d-meier.de/tut22/Kaktus/Seite1.html; http://www.3d-meier.de/
Der Vorteil des Kaktus‘ ist zweifellos, dass man ihm beim Wachsen der Struktur zusehen kann, während der Korb der Sonnenblume fertig aus der Blüte kommt. Der Kaktus verfügt dabei über zwei interessante Gegebenheiten:
– er wächst beim Aufblähen so, dass sich in der Nähe seines Pols neue Stachelwarzen bilden können, die sich den besten freien Raum suchen dürfen (beim Drängeln suchen „müssen“! Siehe Rechteck-Vereinfachung dort!)
– er wächst beim Aufblähen so, dass sich alle seine Oberflächenelemente ähnlich zu sich selbst vergrößern können, was der Form der Über-Spiralen nicht widerspricht:
(Andere Spiralen-Exponenten siehe auch dort!)
Auch die Anordnung auf einer Kugeloberfläche (Kaktus) zeigt in der Projektion noch Spiralen, die nach außen aber enger werden.
Doch woher weiß der Kaktus, wo der richtige neue Warzen-Stachel-Punkt sein muss?
Ist hier wieder ein Perspektiv-Wechsel vonnöten, wie er uns schon bei der Behandlung der Sechs-Eckigkeit der Basaltsäulen geholfen hat??
In der Tat ist das möglich! Wir zeichnen einmal nur die inneren fünf Kaktus-Punkte ein und überlegen, wo ein neuer Platz hätte. Wir erkennen, dass die bisherigen Nummern 2, 3 und 5 in einem Dreieck um einen mathematisch erforderlichen (Winkel um einen Goldenen Winkel zurück, Abstand ebenfalls rückgerechnet) neuen Punkt 0 liegen. Welche einfache geometrische Eigenschaft liegt in der Nähe dieses Punktes? Der Umkreis-Mittelpunkt der drei Punkte 2,3 und 5! Dieser hat den gleichen Abstand zu allen drei Punkten, drängelt also am wenigsten! Ist auch noch die geringe Abweichung von UK-MP und GS-Warzenpunkt zu erklären? JA! Denn erstens sind die drei „alten“ Warzen schon unterschiedlich weit ausgewachsen, wodurch der UK-MP ebenfalls verschoben werden müsste, und zweitens liegt wieder schräg gegenüber (genauer: auf der positiven x-Achse!) die nächst-folgende Warze auf Entwicklungs-Lauer“! Beides veschiebt in jedem Takt den UK-MP in die richtige Richtung. Geometrisch sieht das dann so aus:
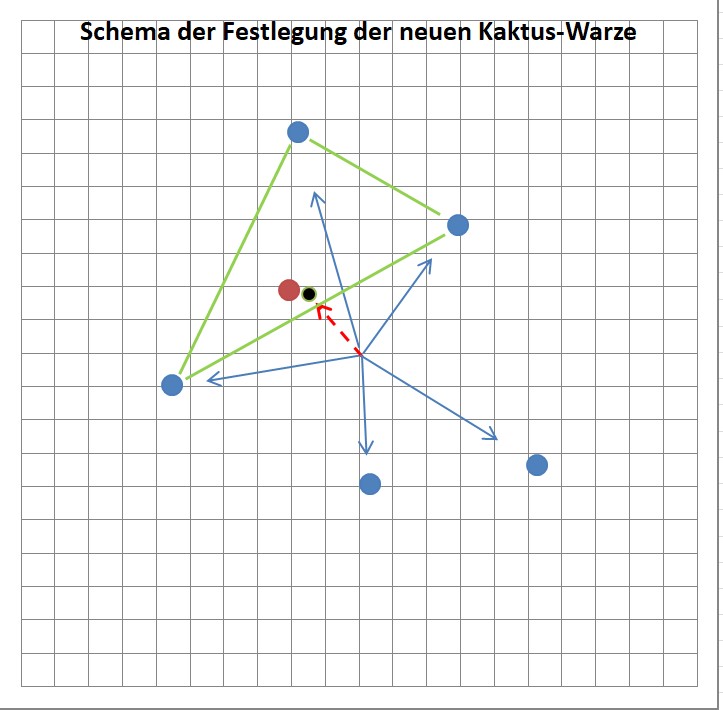
Die oberen drei Punkte sind von links nach rechts die „früheren Warzen“ Nr. 3, 5 und 2, der Rote ist der theoretische neue Warzenpunkt, der schwarze der Umkreis-Mittelpunkt UK-MP des grünen Dreiecks
FAZIT:
Wie schon bei den Basalt-Säulen ist es möglich, durch einen Perspektiv-Wechsel zu zeigen, dass die für den Gewohnheits-Mathe-Menschen kompliziert aussehenden Dinge der Natur „ihrer Natur“ nach eigentlich einfach sind. Der Folgen-Aufbau des Goldenen Schnitts ist über den Fibunacci-Gedanken geometrisch unterschiedlich einfach umsetzbar, eben durch einen Algorithmus, der erst durch seine Wiederholung zu eleganten mathematischen Ausdrücken konvergieren kann und dann auch tatsächlich konvergiert.
Im Abschnitt 1.1.1 wurde ein diskretes Programm vorgestellt, das einem Kegelschnecken-Schalen-Muster sehr nahe kommt:
Quelle: https://ig-meeresaquaristik.de/index.php/Thread/179-Gifte-der-Kegelschnecken/
Quelle: https://www.apotheke-adhoc.de/nachrichten/detail/pharmazie/kegelschnecken-gift-statt-morphium-schmerztherapie/
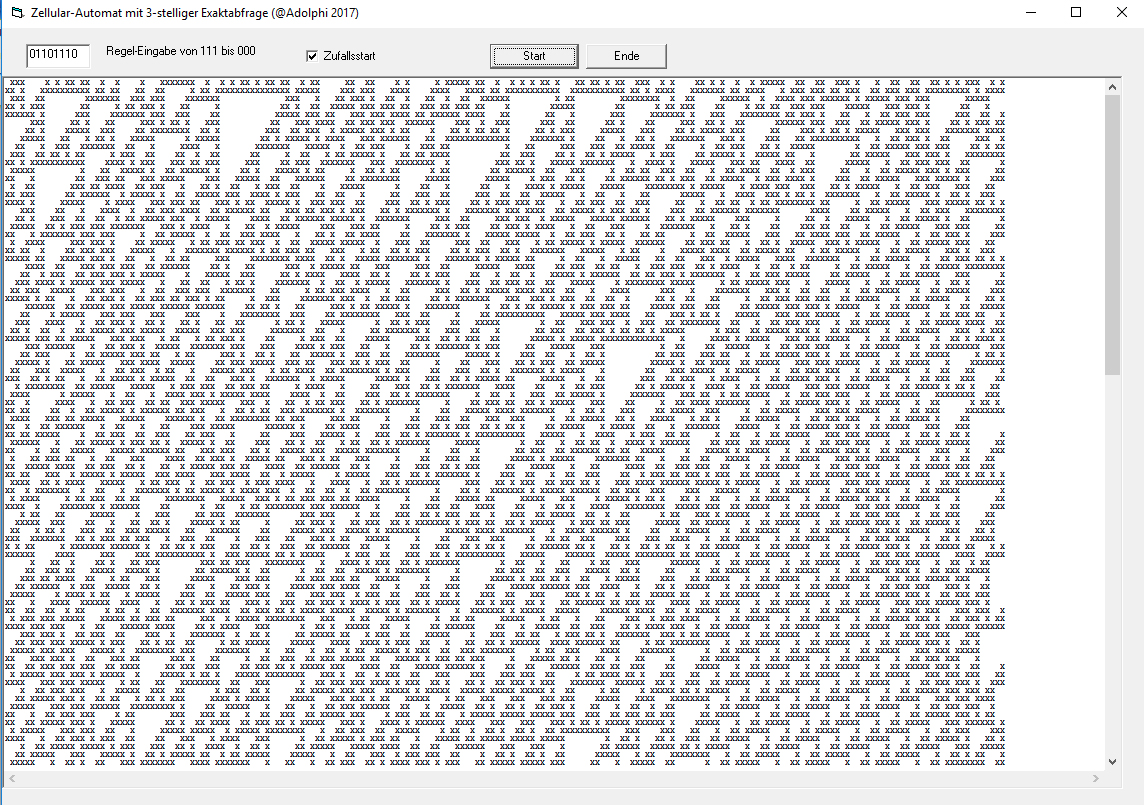
Schiefe Dreiecke und schräge Streifen der Regel (0110 1110) beim endimensionale zellulären Automaten
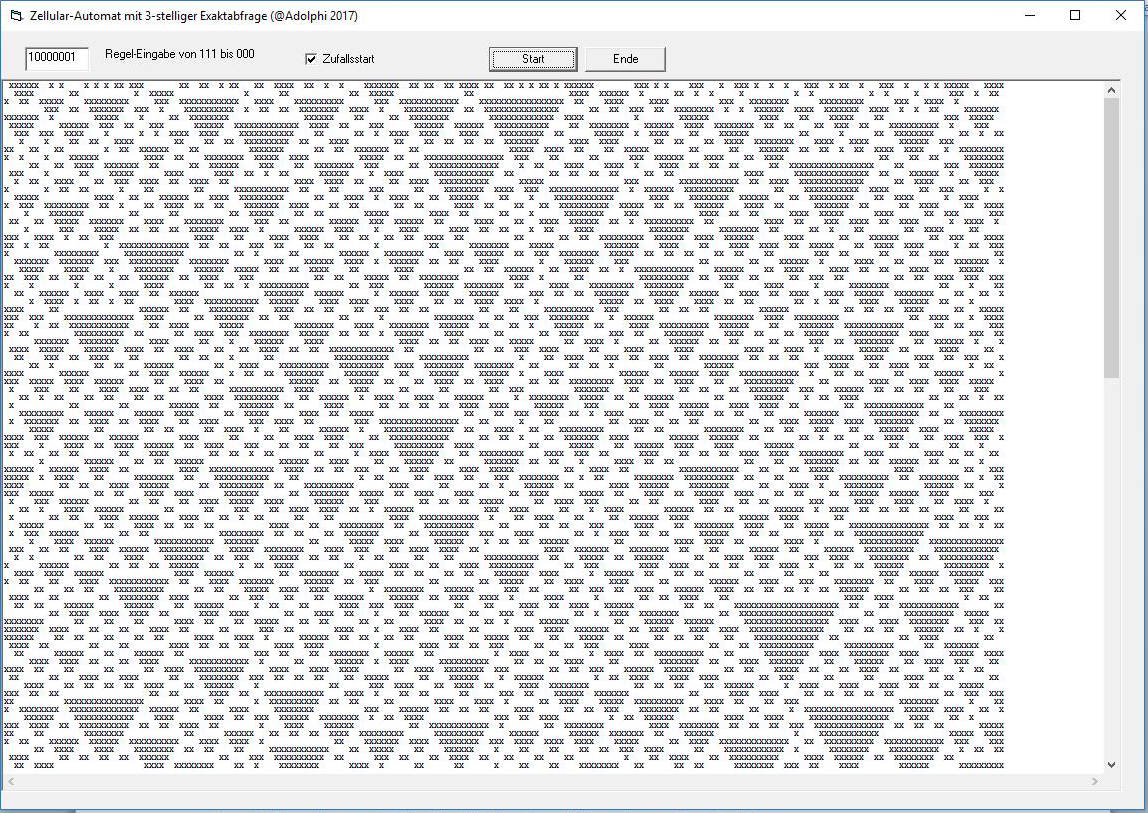
Die Regel (1000 0001) ergibt ebenfalls ein Dreiecksmuster: Existenz nur bei entweder drei oder null Vorgängern.
Das gegenseitige Überlappen aber fehlt. Offenbar ist der genetische Code etwas komplizierter als unser primitiver Computer-Code für die allerersten Muster-Spielchen mit zufälligem Start.
(wird bald fortgesetzt!)









Kommentar abgeben