Problem-Analyse und Lösungs-Synthese
Am allerschwierigsten ist für den Ungeübten die Analyse eines Problems, einer „Textaufgabe“ oder „Sachaufgabe“.
Das heißt, man muss das Zerlegen eines komplexen Erscheinungsbildes in seine einzelnen kausalen Zusammenhänge erst lernen. Erst nach der Zerlegung des Problems können die einzelnen Zusammenhänge bearbeitet und ihre einzelnen „Lösungen“ zur Erklärung des gesamten Erscheinungsbildes wieder zusammengesetzt werden. Am besten gelingt das mit der sehr aufwändigen Methode der schrittweisen „Modellierung“. Aber manchmal genügt schon eine Näherung mit analytischen Ansätzen, um sich ein Bild vom Gesamtzusammenhang zu machen.
(An meinen Studenten erlebe ich immer wieder, dass die Hoffnung, für eine zusammengesetzte Problemstellung einen fertigen Lösungsansatz in einer Formelsammlung finden zu können, trotz vieler Such-Misserfolge nicht totzukriegen ist. In den folgenden Beispielen wird also der „echte“ Zick-Zack-Weg des Findens von Lösungen dokumentiert, mit allen typischen Fehlern, Trugschlüssen und Umwegen. Das ist somit ausdrücklich NICHTS zum Durchblättern für Sucher schneller Lösungen!!)
Beispiel 1
Beispielhaft betrachten wir einmal ein Glas Bier oder ein Glas Sekt oder Radler oder Limonade oder Sprudelwasser oder anderes CO2-haltiges Getränk:
Wird das Getränk aus einem Druckgefäß in ein Glas umgefüllt, sehen wir Perlenschnüre von Blasen aufsteigen.
Es kommt nun auf den Betrachter an, ob er sich über das konkrete Erscheinungsbild wundert oder ob er es schon immer (also gewohnheitsmäßig) einfach „hingenommen“ hat, dass da Blasen aufsteigen. Die Erwartungshaltung (das „Vorurteil“), dass da Blasen aufsteigen „müssen“, ist durch die Praxis bestätigt worden und basta.
Schaut man aber genauer hin, so gibt es doch ein paar Dinge, die verblüffen:
- es gibt Perlenschnüre aus winzigen Blasen, die beim Aufsteigen nicht größer werden
- es gibt Blasen, die größer und schneller werden beim Aufsteigen
- es gibt schnurgerade Perlenschnüre
- es gibt sich schlängelnde Perlenschüre
- es gibt ….
Alles passiert im selben Glas. Was ist da los? Kann man das verstehen? (Wenn ich diesen Blasenschnüren träumend zusehe, fragen mich meine Freunde, warum ich so traurig sei und mich nicht am Gespräch beteilige…)
Schritt 1: Suche nach Zusammenhängen, die eine Rolle spielen „könnten“
- Dass die Perlenschnüre von unbewegten Startpunkten ausgehen, könnte ein Hinweis auf „heterogene Keimbildung“ (Unebenheiten des Glases oder Verschmutzung) sein.
- Der Auftrieb einer Blase sollte in erster Näherung nur von ihrem Volumen abhängen.
- Das Volumen einer Blase hängt von der eingeschlossenen Gasmenge und dem Druck ab.
- Der Druck in einer Blase hängt von ihrer Krümmung (Oberflächenspannung) und dem Außendruck (Luftdruck plus hydrostatischer Druck) ab.
- Die Gasmenge in einer Blase wechselwirkt mit dem gelösten Gas in der Flüssigkeit, es gibt also einen Austausch, dessen Geschwindigkeit wiederum vom Partialdruck in der Blase und der Konzentration in der Lösung abhängt.
- Die Geschwindigkeit einer Blase sollte vom Auftrieb, der Reibung und dem „Windschatten“ vorausgehender Blasen abhängen.
- Die offensichtliche, aber kurzzeitige Formstabilität der Schlängelung mancher Schnüre deutet sowohl auf auslenkende als auch auf rücktreibende Kräfte hin.
Alle diese Zusammenhänge lassen sich in Gleichungen formalisieren (und nun endlich auch in Formelsammlungen finden!!). Einige davon sind Differentialgleichungen, wiel sie nur Geschwindigkeiten beschreiben (räumliche und solche von anderen Änderungen). Man kann mit Sicherheit ein System von Differenzengleichungen aufstellen, das sich numerisch integrieren lässt und somit zu einer Modellierung führt, deren Ergebnis (grafisch dargestellt) mit der Realität übereinstimmen sollte, wenn die Modellierung realitätsnah parametrisiert worden ist.
Schritt 2: Schrittweiser Aufbau der Modellierung
Ganz allgemein kann man sagen, dass die Reihenfolge der Schritte beim Modell-Aufbau in mehrfacher Hinsicht eine Rolle spielen kann:
– eine Plausibilitätsprüfung pro Schritt ist dann am einfachsten, wenn man mit dem „Groben“ beginnt und schrittweise verfeinert (setzt aber eine Abschätzung der Größenordnung der einzelnen Teil-Einflüsse voraus!)
– eine Steigerung von einfach zu formulierenden Einflüssen zu komplexeren lässt den Mut des Modellierers nicht zu schnell sinken und hat auch den Vorteil der anfänglich einfachen Prüfung des Einflusses der gewählten freien Parameter
Für unser Bierblasen-Modell heißt das, dass man (2.1) zuerst einmal nur den Zusammenhang zwischen Gasmenge, Druck und Volumen (und damit Radius bei angenommener isometrischer Form, also Kugel) untersucht, dann (2.2) die Geschwindigkeit hinzunimmt, schließlich (2.3) den Gasaustausch mit der Flüssigkeit modelliert und dann (2.4) die Wechselwirkung der Blasen untereinander zulässt. Dann wäre zwar das interessanteste Phänomen erst zum Schluss dran, aber man hätte dafür vorher klare Vergleichsmöglichkeiten mit der Natur, um das Modell zu „fitten“.
Schritt 2.1: Druck in der Gasblase
Der Innendruck pi in der Gasblase setzt sich aus drei Komponenten zusammen (siehe oben vierter Zusammenhang):
– Luftdruck po, der auf der Flüssogkeitsoberfläche lastet (konstant als 100.000 Pa angenommen)
– hydrostatischer Druck ph, der von der Höhe der Flüssigkeitssäule h, der Dichte rho der Flüssigkeit (1 g/cm³) und der Erdbeschleunigung g (10 m/s²) abhängt:
ph = rho * g * h
– von der Oberflächenspannung gamma (0,07 N/m für Wasser an Luft) herrührender Innendruck, der von der Krümmung der Oberfläche (Kugel mit Radius r) abhängt:
ps = 2*gamma/r
Geht man davon aus, dass bei konstanter Temperatur das Produkt von Druck und Volumen einer Gasmenge konstant ist, so kann man alles auf eine Blase bei Luftdruck beziehen, indem man ihre dortigen Werte mit Vo und ro und po bezeichnet.
po*Vo = pi*Vi
Mit dem Kugelvolumen V = 4/3*pi*r³ ergibt sich dann für den Innendruck pi
pi = po + ph + ps
und
po*Vo = (po + ph + ps)*Vi
oder
po/(po+ph+ps)*ro³ = ri³
und wegen der Abhängigkeit des ps von ri
(Glg. 1): (po + rho*g*h) * ri³ + 2*gamma * ri² – po*ro³ = 0
Diese Gleichung zeigt schon durch ihre „Struktur“, dass es ein ri geben kann, wo sich die Wirkungen der dritten und zweiten Potenz von ri in ihrer Wichtigkeit abwechseln. Wir haben es also mit einem klassischen Beispiel dafür zu tun, dass unterschiedliche „Dimensionszahlen“ die realen Erscheinungsformen eines allgemeinen Zusammenhanges bestimmen können.
Setzt man die oben erwähnten Größen in die Gleichung ein und setzt überschlagsweise ro=ri, kommt man zu dem Ergebnis, dass zwischen 1 und 10 Mikrometer Blasenradius bei einer Wassertiefe (oder Biertiefe) von 20 cm (hohes Glas, aber trotzdem nur unwesentliche 2% vom Luftdruck…!) der Druck durch die Oberflächenspannung dem Luftdruck vergleichbar wird:
(po + rho*g*h) = 102.000 N/m²
2*gamma/ri = 0,14 N/m / ri
po = 100.000 N/m²
Damit der zweite Wert mit den anderen beiden in die gleiche Größenordnung kommt und dadurch die linke Seite der Gleichung 1 wesentlich von 0 verschieden macht und eine Neu-Berechnung (anstelle der Näherung ro=ri) von ri erzwingt, muss ri=ro etwa 0,00001 m = 10 um oder noch kleiner sein.
Im Umkehrschluss zeigt aber schon diese Überschlagsrechnung, dass die beobachtete Zunahme der Größe großer Blasen und das Gleichbleiben der Größe sehr kleiner Blasen NICHT mit dem sinkenden hydrostatischen Druck beim Aufsteigen zu tun haben kann, denn das müsste erstens ziemlich größenunabhängig und zweitens bei 20 cm Tiefe als Start im Bereich der 3. Wurzel des Volumenverhältnisses von 1,02 sein, also bei einem nicht mehr erkennbaren Radius-Zuwachs von weniger als 1% liegen.
Für die exakte Lösung der kubischen Gleichung (1) gibt es verschiedene Verfahren, analytische (Cardanische Formel zum Beispiel) und numerische (Newton-Verfahren zum Beispiel). Bei der Modellierung ist sicher die numerische Variante vorzuziehen, wie sie auch hier verwendet worden ist.
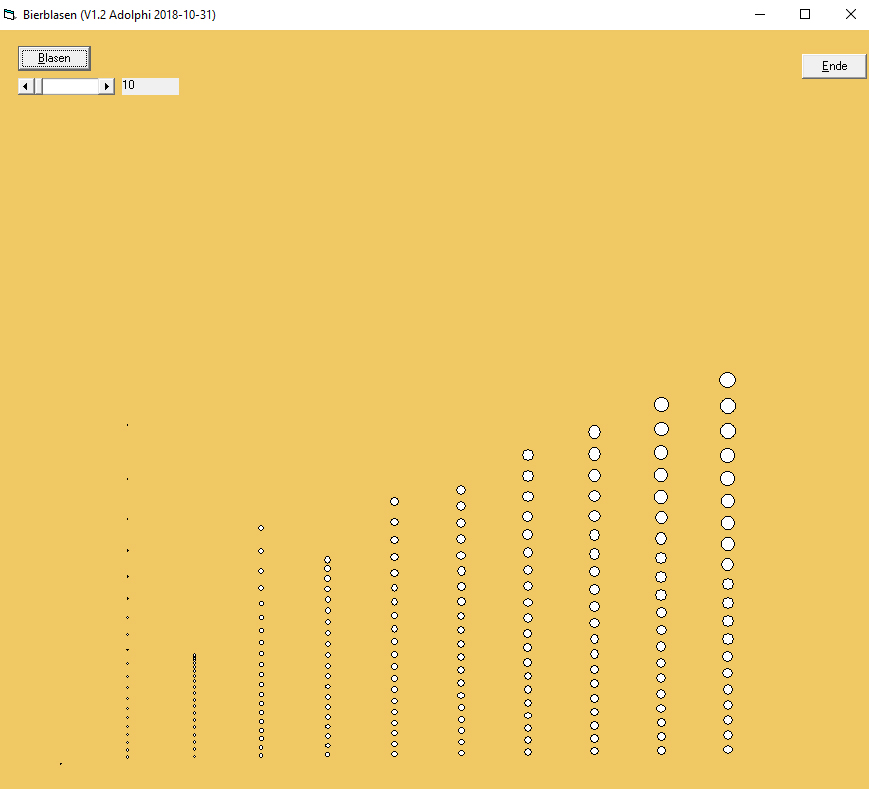
Hier das Ergebnis der Berechnungen für logarithmisch gestaffelte Wassertiefe und Normaldruck-Radien der Blasen:
Die typische Bier-Tiefe in einem Bierglas (20 cm) ist die 5. weiße Teilungslinie von links. Die dort kreuzenden weißen Linien der Blasen unterschiedlicher Normaldruck-Radien (von 1 um bis 5 mm ebenfalls logarithmisch) haben quasi konstante Radien bis 20 cm Tiefe und werden erst ab 1 m deutlich zusammengequetscht! UND: Nur unterhalb von 50 um Radius (5. weiße Teilungslinie von vorn) spielt die Oberflächenspannung eine merkliche Rolle, quetscht die Blasen also um mehr als 1% des Radiusses!
Schritt 2.2: Geschwindigkeit der Gasblase beim Aufsteigen
Da die Dichte des Gases etwa bei einem Tausendstel von der des Wassers (Biers) liegt, kann man ihre Masse gegenüber der des zu verdrängenden Wassers vernachlässigen und von einer sehr schnellen Erreichung der Gleichgewichts-Geschwindigkeit ausgehen.
Der Auftrieb als treibende Kraft der Bewegung ist Volumen-Proportional, der Wasser-Widerstand als Gegenkraft Querschnitts-proportional. Daraus sollte sich eine linear radiusabhängige Gleichgewichts-Geschwindigkeit ergeben.
Daraus wiederum sollte sich der Abstand von in konstantem Zeittakt erzeugten Blasen bei wachsender Größe der Blase innerhalb der beobachteten Perlenschnur ebenfalls vergößern, was der Beobachtung entspricht.
Die Gasblasengröße MUSS aber für ihr Wachsen einen anderen Grund als den des hydrostatischen Druckabfalles haben, da wir diesen oben ausgeschlossen haben. Sie kann also nur noch durch zusätzliche Aufnahme von gelöstem Gas wachsen. Nimmt man an, dass dieser Übergang proportional der Blasenoberfläche UND proportional der Übersättigung (Differenz von tatsächlichem „Partialdruck“ des gelösten Gases und Innendruck der Blase) ist, so wächst das Volumen zwar proportional zur Übersättigung UND quadratisch mit dem Radius, aber der Radius selbst wächst dann nur einfach proportional mit der Übersättigung (wieder einmal der hochinteressante Dimensionsunterschied!). Und da, wie oben schon erwähnt, der Druckanteil der Oberflächenspannung (besser eigentlich: Grenzflächenspannung) mit zunehmender Größe rapide abnimmt, wachsen deutlich überkritische Blasen zeitproportional im Radius, kritische gar nicht und die dazwischen liegenden beschleunigt.
Die Differenzengleichungen für eine numerische Rechnung sind somit linear:
neuer Radius = alter Radius + Konstante1 * Übersättigung * Radiusdifferenz zum Gleichgewichtsradius*Zeittakt:
(Glg.2) ri(t+dt) = ri(t) + k1*ü*(ri(t)-rk)*dt
neuer Blasenort = alter Blasenort + Konstante2*Radius*Zeittakt:
(Glg.3) z(t+dt) = z(t) + k2*ri(t)*dt
In der Konstanten stecken die Materialgrößen und der Zeittakt. In einem kleinen Biervolumen nimmt natürlich streng genommen die Gasübersättigung mit der Zeit durch die Blasenbildung selbst ab, das Bier wird dann schal und perlt nicht mehr. Aber uns geht es ja hier um ein Augenblicksbild. Wir nehmen also eine genpügend große Biermenge…
Macht man aus diesen Angaben nun das gewünschte „Augenblicksbild“ einer Reihe von Perlenschnüren von Blasenquellen konstanter gleicher Frequenz, aber unterschiedlicher Blasengröße (die Kerne für die heterogene Keimbildung sind also unterschiedlich gestaltet), ergibt sich folgendes Bild mit von links nach rechts wachsender Startgröße:
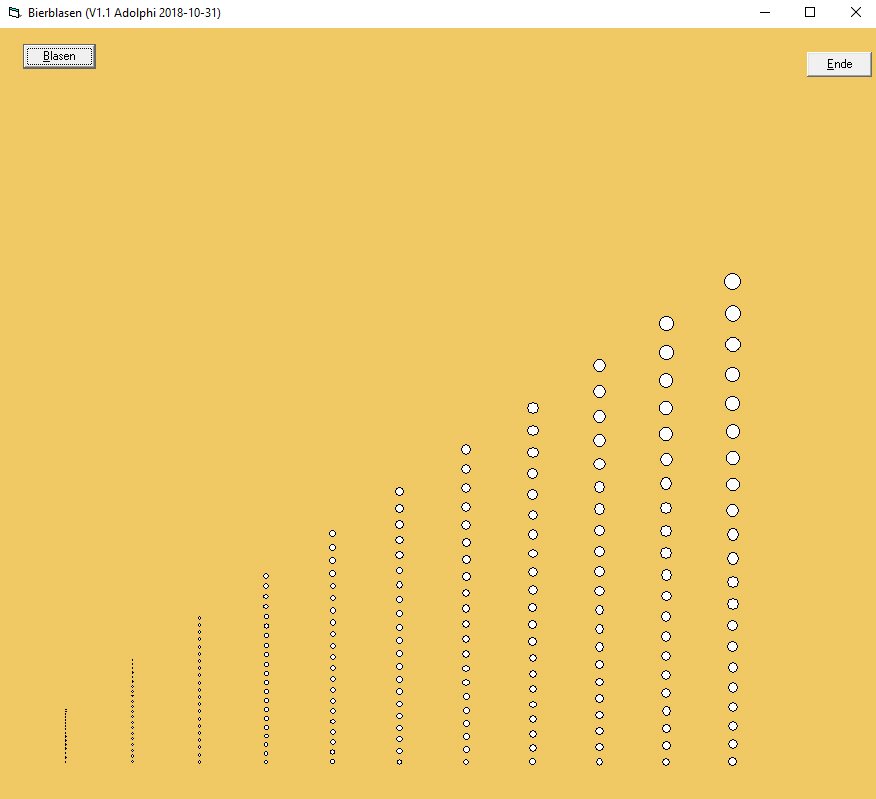
Bierblasen-Schnüre mit größenproportionaler Geschwindigkeit und größenabhängiger Wachstumsrate, aber ohne Wechselwirkung untereinander: Innerhalb einer Schnur ist das Verhältnis von Größe und Abstand der Blasen konstant. (Die kleinen sind unterkritisch gewählt und verschwinden, die großen wachsen gut.)
Es sieht schon „beinahe fast“ wie in der Wirklichkeit aus. Dort hat man aber den Eindruck, dass die Geschwindigkeit noch schneller wächst und die Blasenabstände nach oben also noch schneller als nur proportional zum Radius wachsen. Das muss am „Windschatten“ liegen! Also weiter:
Schritt 2.3: Versuch der Modellierung einer gegenseitigen Beeinflussung der Blasen
Zuerst untersuchen wir den Windschatten nur in der Hauptbewegungsrichtung von unten nach oben, ohne seitliche Komponente, also ohne Auslenkung.
Hier ergibt sich ein interessant zusammengesetzter Zusammenhang, der aus dem Muskel-Sport bekannt ist (Radfahren, Schwimmen, Skilaufen):
Je schneller der Vorauseilende, desto größer die Windschattenwirkung. In der Kette bedeutet das, dass auch der Vorauseilende schneller werden könnte, wenn er selber einen Vorauseilenden hätte (nur der Führende „steht“ im Wind oder im ganzen Wasserwiderstand). Das sieht wie eine positive Rückkopplung aus und ist auch eine, was dazu führen muss, das der Führende überholt wird. Lässt man nun im Modell keine große Reichweite zu, so dass nur der jeweils eine davor sich Bewegende den Schatten bietet (die Wirkung des übernächsten wird also vernachlässigt), ergibt sich trotzdem eine Fortpflanzung der Wirkung auf dem Umweg über die Geschwindigkeit, denn der Zweite ist schneller als der Erste und bietet damit dem Dritten eine höhere Schattenwirkung als er selbst erfährt und so weiter…
Im Sport wird das dadurch negativ überlagert, dass die dahinter sich bewegenden auf eine höhere Geschwindgkeit verzichten und stattdessen Kraft (besser: momentane Leistung als Kraft mal Geschwindigkeit und über die Zeit somit Energie) sparen. Das „können“ die Blasen aber nicht!
Wir müssen also eine ordentliche Kräfte-Bilanz aufstellen: Auftriebskraft, Reibungskraft im ruhenden Medium, Windschattenkraft. Abweichend von sonst üblichen Rechnungen fehlt hier die Trägheitskraft, weil wir die Blasenmasse vernachlässigen, und somit davon ausgehen, dass sich die Gleichgewichts-Geschwindigkeit augenblicklich einstellt. Lassen wir auch noch die „führende Blase“ weg, gehen also von einem stationären Zustand aus, so ergibt sich folgender Zusammenhang zwischen den drei gerichteten Kräften:
Reibungskraft (Geschwindigkeit, Größe (Zeit)) + Auftriebskraft (Größe(Zeit)) + Schattenkraft (Geschwindigkeit, Abstand, Größe(Zeit)) = Null
Man könnte die erste und die dritte Kraft mit geeigneten Koeffizienten zusammenfassen, wenn beide Partner genähert die gleiche Größe hätten. Da aber gerade die Größen- und Geschwindigkeitsentwicklungen von Interesse sind, müssen wir auf diese Vereinfachung verzichten. Über die Zeit kommen wir aber im stationären Fall aus der Geschwindigkeit auf eine neue Ortsabhängigkeit der Blasengröße und des Blasenabstands.
Glg.4 ist viel komplizierter, als sie auf den ersten Blick aussieht, selbst dann, wenn man die Reibungs- und die Schattenkraft nur einfach linear von der Geschwindigkeit abhängig sein lässt:
(Glg.4) Fr + Fa + Fs = 0
Fr(t,ri) = – k3 * v(t) * ri²(t) (ri kompliziert nach den Zusammenhängen ganz oben in Glg.1 oder Glg.2 zu berechnen)
Fa(ri) = k4 * rho * g * ri³(t)
Fs = k5 * v(t) * ri²(t)/(dz) (mit dz als Abstand zur vorausliegenden Blase)
dh ist selbst wieder von der Geschwindigkeit abhängig, wenn wir von einer konstanten Blasenbildungsfrequenz f (wie oben schon) ausgehen:
dz = v(t)/f
Damit wird die Gleichung für Fs einfach
Fs = k5 * f * ri²(t)
und die Gesamtgleichung sieht so aus:
(Glg.4a) (k4*rho*g) * ri³(t) + (k5 * f – k3 * v(t)) * ri²(t) = 0
Ohne Ärger dürfen wir durch den von Null verschiedenen Radius teilen und umstellen:
k4*rho*g * ri(t) + k5 * f – k3 * v(t) = 0
(Glg.4b) v(t) = (k4*rho*g * ri(t) + k5 * f) / k3
Die Differenzengleichung für den Blasenort z unterscheidet sich nun von Glg.3 durch einen konstanten Zusatzterm k7, der die Blasenbildungsfrequenz enthält:
(Glg.3) z(t+dt) = z(t) + k2*ri(t)*dt
(Glg.5) z(t+dt) = z(t) + (k6*ri(t)+k7)*dt
Damit kann nun auch der Blasenabstand zwar schneller,aber auch nur linear wachsen! Was passiert also, wenn wir die Widerstandskräfte (auch den Winddschatten also!) nichtlinear von der Geschwindigkeit abhängig sein lassen?
Würde also v(t) nicht in der ersten, sondern zum Beispiel in der 1,4-ten Potenz stehen, lautete Glg.5 als Glg.5a ganz anders:
(Glg.5a) z(t+dt) = z(t) + ((k6*ri(t)+k7)*dt)^(1/1,4)
Das ist alles blöd – ich muss neu nachdenken.
WARNUNG: Bisher ist alles nur Visualisierung, NICHT Modellierung, denn es wird keine konkrete Wechselwirkung mit dem individuellen Nachbarn errechnet, sondern der Weg einer Blase stellvertretend für alle berechnet und getaktet dargestellt, weil nach diesem Ansatz jede Blase gleich ist und ein zeitgetaktetes Bild einer einzigen Blase mit dem Augenblicksbild vieler Blasen identisch ist.
Folgendes gutes Bild erhält man auf diese Quasi-Weise, wenn man vor allem den Windschatten radiusabhängig macht, die Vereinfachungen der obigen Formel Glg.5 also aufhebt:
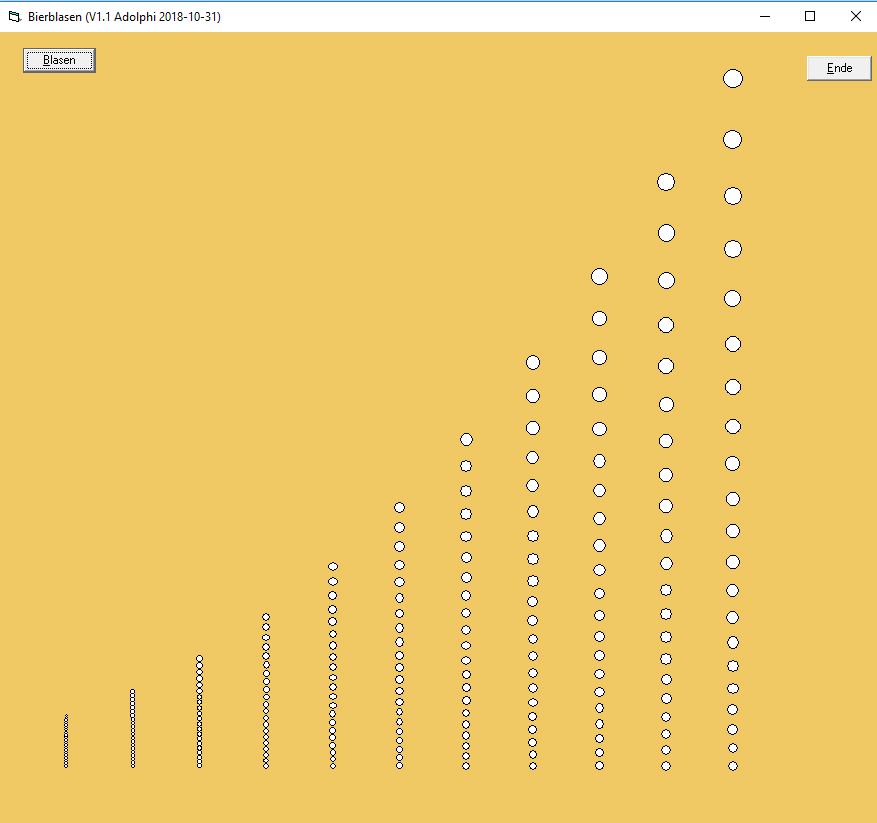
Überproportionale Geschwindigkeit durch verallgemeinerten (nicht diskretisierten!) Windschatten erhöht den Blasenabstand
Was ist die Physik dahinter? Bei einer reibungsfreien laminaren Umströmung kann man ganz auf Widerstand oder Windschatten „verzichten“. Lässt man aber Reibung zu, so hat zwar immer noch die Luftblase quasi keine Trägheit, wohl aber das verdrängte Wasser (Bier). Seine Wirbel sind auch noch hinter der vorbeigekommenen Blase vorhanden und die resultierende lokale Strömung wird in der Mitte der Spur im wesentlichen nach „vorne“ zeigen. Das wird mit dem Abstand exponentiell abnehmen. Man kann dann zusammengefasst etwa annehmen, dass direkt hinter der Vorläuferblase gar kein Widerstand existiert und nach einem bestimmten Abstand als spezielles Vielfaches des Produktes von Radius und Geschwindigkeit (Ähnlichkeitsprinzip: Halbwerts-Abstand) ein exponentieller Anstieg auf den halben „Widerstand ohne Vorläufer“ erreicht ist. Auf diese Weise sollte sich ein Abstand ergeben, der sowohl vom Radius als auch der Geschwindigkeit abhängt.
Aber: Man muss tatsächlich jede Blase einzeln in Abhängigkeit von ihrer Geschichte (sich daraus ergebende aktuelle Größe) und ihrem Vorgängerabstand (Geschwindigkeit) berechnen. Der Zeittakt muss dann so eng sein, dass es keine artefaktischen Schwingungen des Abstandes (Überschwingen der numerischen Berechnung) gibt.
Blasengröße nach obigem Ansatz:
Blasenradius = (Zeitintegral über die Differenz zum kritischen Radius) mal Konstante
oder differentiell:
dr = k8 * (r-rk)/r * dt = k8 * (1-rk/r) * dt
Aufstiegsgeschwindigkeit nach neuem Ansatz:
Blasengeschwindigkeit = Eigengeschwindigkeit (vom Radius linear abhängig) + Windschattengeschwindigkeit (vom Abstand zum Vorläufer (mit Index i-1 charakterisiert) exponentiell abhängig)
v(i) = vo(i) + v(i-1)*exp(-a/ao) mit ao als charakteristischem Abstand für v(i-1)/e
Dieser Ansatz allein wäre wegen seiner positiven Rückkopplung des Abstandes
a(t+dt) = a(t) + (v(i-1)-v(i))*dt
wegen v(i)>v(i-1)
unsinnig für die Erzeugung eines stabilen Zustands, weil dann jede Blase ihre Vorgängerin einholen und sogar überholen müsste, sofern diese keine bessere Vorgängerin hat (dann würde sie zunehmend zurückfallen und „abreißen lassen müssen“. Eine stabiler Zustand erforderte notwendig (noch nicht hinreichend!) eine negative Rückkopplung! Das bedeutet im Umkehrschluss:
1. Stationäre Blasenstränge sind NICHT durch Windschatten zu charakterisieren.
2. Windschatten mit dem hier benutzten Ansatz führt schon zu Instabilitäten, ohne dass man Wirbel einführen muss!
Es gibt noch eine zweite Bedingung für den stabilen (stationären Endzustand), dass nämlich Geschwindigkeit und Abstand die Bildungsfrequenz ergeben müssen, da unterwegs keine neuen Blasen entstehen.
a = z(i-1) – z(i) = v(i-1) / f
oder
v(i-1) = a*f
Damit ergäbe sich nun mit
v(i) = f(r(t)) = vo(r(t))(i) + a*f*exp(-a/ao)
ein eindeutiger momentaner Zusammenhang für jede Blase mit einem scheinbar freien Parameter a als unabhängige Variable. Da aber a die Verknüpfung mit der Nachbarblase darstellt und diese der gleichen Bedingung genügen muss, steht in Wirklichkeit ein Gleichungssystem für verschiedene Blasen (also implizit für verschiedene Zeiten!) da.
Für die Modellierung müssen alle Orte, Größen und Geschwindigkeiten aller Blasen als Daten vorgehalten und ständig neu berechnet und dargestellt werden, wie das in einem echt diskretisierten Modell erforderlich ist. Der Aufwand wächst enorm, dafür wächst auch der Grad der Unabhängigkeit des Modells von a-priori-Einstellungen. Es ist wegen der eigenartigen Rückkopplung also mit gewaltigem Durcheinander zu rechnen. Mal sehen…
Zuerst der zeitabhängige Blasenradius mit dem Parameter seiner relativen Größe zur kritischen Blase (die ist im Gleichgewicht mit der übersättigten Umgebung):
Die kritische Blase wächst nicht, die größeren gehen allmählich in ein konstantes Wachstum über (obigen Überlegungen entsprechend!), die kleineren „verdampfen“ beschleunigt.
Ist man noch faul und übernimmt das alte Quasi-Modell mit der Berechnung aller Blasen von unten nach oben, so ergeben sich schon leichte Instabilitäten (stärkere schwingen sofort total über!!) im Blasenbild:
Es muss also eine echte Diskretisierung erfolgen, indem die Blasen nacheinander erzeugt werden und dann wandernd von oben nach unten wechselwirken, während hier noch lediglich die Abstände und Größen interagierend zum selben „Zeitpunkt“ erzeugt werden, der Integrationsprozess also stark abgekürzt stattfindet.
Übrigens: Man darf sich jetzt erinnern, dass es auch den umgekehrten Fall gibt (Wasser in Luft statt Luft in Wasser):
Tropfen-Schnüre von Wasserhähnen, Dachrinnen, durchhängenden Telegrafenleitungen, Grashalmen an Felsvorsprüngen etc. Wenn es einem gelingt, mit dem Auge dicht neben die Schur zu gelangen und unter sich eine große Falltiefe zu haben, so kann man mit geringer Parallaxe dem Treiben der Tropfen zusehen:
- die Nachfolger holen die Vorgänger durch Windschatten ein
- es erfolgt entweder ein Kreiseln umeinander oder eine Vereinigung
- nach der Vereinigung kann der Tropfen so groß sein, dass er schwingt oder sogar zerplatzt
Es lohnt sich also, tatsächlich einen echt diskretisierten Ansatz zu wagen (bei den Tropfen käme die Trägheitskraft – Berücksichtigung ihrer individuellen Masse – noch dazu).
(geht bald weiter, muss erst wieder programmieren!)