4.1.1.2 Fehlleistungen trainierter Strukturen
Es ist gut, dass wir bewusst und unbewusst trainierte Leistungen abrufen können, um den Kopf für andere Dinge frei zu haben.
Das ist aber auch die Basis für diverse Täuschungen, wenn trainierte Zuodnungen auf Situationen angewendet werden, wo sie nicht passen. Das bekannteste Feld dafür sind die optischen Täuschungen, bei denen das trainierte Umdeuten von zweidimensionalen Bildern in dreidimensionale Realitäten in die Irre geführt wird.
Ich will hier nicht raffinierte Fälle vorstellen, sondern mich im Gegenteil an die Basis der Sache heranpirschen.
Nehmen wir den einfachen Fall eines schiefen Vierecks. Man hat zwei Möglichkeiten einer Unterteilung in kleine Vierecke (Parkettierung mit ähnlichen Vierecken ist unmöglich):
- konstante Teiling der Viereckseiten
- konstante Teilung des Winkels gegenüberliegender Seiten
Das sieht dann so aus:
Es fällt auf, dass in beiden Fällen das Viereck (unterschiedlich!) verzerrt erscheint, also als eine im Raum gebogen Fläche. Die Folge ist zum Beispiel, dass die Fluchtpunkte falsch erscheinen. Durch Anlegen eines Lineals kann man sich aber überzeugen, dass sie richtig liegen. Das gemischte Bild ist am schwersten umzuinterpretieren, weshalb die Fluchtpunkte „richtiger“ erscheinen. (Schon die alten Kupferstecher haben durch Schraffuren die interessantesten Wölbungen darstellen können…)
(Übrigens sind diese einfachen Schraffur-Vorschriften auf konvexe Gebilde beschränkt.)
Das Training der Zuordnung von optischen Eindrücken der Umgebung und dieser selbst findet mit Hilfe des Tastsinns der Säuglinge statt (Der später in der Schule konstruierte Konflikt durch „auf dem Kopf stehende“ Bilder der Netzhaut ist unsinnig, da die Drehung eines Fotos auf einem Abbildungsuntergrund – Iphone z.B. – keinerlei Umordnung der Bezüge der abgebildeten Objekte untereinander zur Folge hat, wie jedes Kind weiß.), mithin im „nonverbalen“ Alter. Spätere Änderungen der Zuordnungs-Algorithmen – berufich oder sportlich herausgefordert – sind viel schwieriger zu trainieren. Tiere, die sich im Dreidimensionalen bewegen (Luft oder Wasser), sind da besser gewappnet als wir Menschen. (Uns fällt sogar das zweidimensionale Einparken schwer, wenn kein virtueller Draufblick aus der dritten Dimension samt seinen Beziehungen zu den Handlungsabläufen trainiert ist.)
Genau genommen beginnt der Interpretations-Konflikt aber auch schon dann, wenn es gar nicht um die Zuordnung zu einer weiteren Dimension geht, nämlich in Fällen, wo eine rein 2-dimensionale Gegebenheit in 2 Erscheinungen gegliedert ist: Rand und umrandete Form oder Objekt und Zwischenraum. Der Übergang kann dann fließend gestaltet werden, um an sich selbst zu prüfen, wo der Umschlag stattfindet.
Hierzu ein einfaches Beispiel von Quadraten mit konstanter Strichstärke, deren Seitenlänge variabel ist und stetig zunimmt:
Man sieht, dass man unwillkürlich eine ordnende Priorität setzt: „Schwarze Quadrate auf hellem Grund“ bis „weiße Quadrate auf dunklem Grund“, dazwischen irgendetwas wie „dunkle Rahmen“ oder diverse „Gitter“. Daraus erwachsen noch nicht unmittelbar Interpretationsfehler, aber die unwillkürliche „Ordnung“ (=Prioritätensetzung) kann als Ausgangspunkt für bewusste „Irreführung“ in der bildenden Kunst oder der Werbung genutzt werden. Dass man dabei mit einem einzigen Parameter (hier die Strichstärke der Quadrate) große Effekte erzielen kann, zeigen die folgenden beiden Bilder im Vergleich zu oben (auch hier ein linearer Zusammenhang mit den Koordinaten einem radialen gegenübergestellt):
Nun kann man nun auch ein „helles Gitter“ in einem gewissen Streifen der Darstellung als Priorität erachten.
Sehr beliebt sind die optischen Täuschungen, die, unter Verzicht auf geometrisch exakte Projektion, durch Schraffur eine Zweideutigkeit in der räumlichen „Entscheidung“ offen lassen, wie die allseits bekannten Würfelstapel: (z.B. unterhttps://www.featurepics.com/online/Isometric-Cube-Pattern-3354810.aspx) .
Hier nun aber eine historische Version, die viel interessanter ist: (https://www.illusionen.biz/blog/?page_id=129) Bodenfliesen in der Basilika von St. John Lateran in Rom. (Es entsteht der Eindruck von zwei unabhängig beleuchteten Systemen dreidimensionaler Quader.)
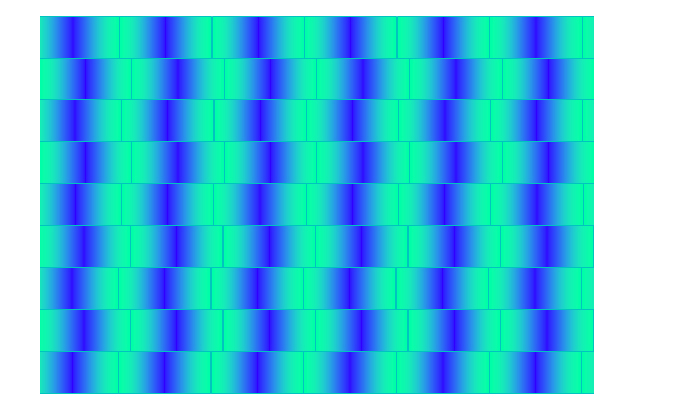
Auch durch Farbübergänge können 2-dimensionale Bezüge „verändert“ und quasi-3-dimensional „aufgelöst“ werden (https://de.wikipedia.org/wiki/Optische_T%C3%A4uschung), was bei einer Rück-Trafo ins 2-dimensionale zu scheinbaren Verzerrungen führt:
(die waagerechten Streifen sind exakt parallel!)
Es gibt Hunderte weiterer interessanter Beispiele im Internet.









Kommentar abgeben