2.1.1 Oberflächen-Risse

getrockneter Nilschlamm (von Wikipedia: bertramz)
Frage:
Kann man die im Alltag häufig beobachtete Struktur der Oberflächenrisse begreifen oder sogar modellieren?
Wenn sich ein äußerlich stetiges Medium zusammenzieht, weil es trocknet oder weil es abkühlt, so muss es reißen, sofern es irgendwo am „Rand“ oder am Untergrund festgehalten wird (ein Eierkuchen auf der fettigen Pfanne tut das üblicherweise nicht).
Hier fängt die spannende Physik an, wenn es denn doch eine Einspannung am Rande oder im Untergrund des sich zusammenziehenden Mediums gibt:
Es baut sich eine mechanische Spannung auf, die irgendwann die Festigkeitsgrenze übersteigt, und es kommt zum Riss. (In meinen Lehrveranstaltungen habe ich gern danach gefragt, welche Temperaturdifferenz durch Abkühlung notwendig ist, damit ein heiß eingespannter Stab beim Abkühlen reißt. Das ist das einfache eindimensionale Problem!)
Hier gibt es also immer einen kleinen Gegenspieler: die Festigkeit. Sonst würde der Riss ja schon beim kleinsten Anlass kreuz und quer laufen, was er aber offensichtlich nicht tut.
Es hat sich herausgestellt, dass eine energetische Sicht aufs Ganze oft hilfreich ist. Einen Riss zu erzeugen, kostet Energie, man muss nämlich die Bindungsenergie zwischen den beiden Riss-Rändern aufbringen. Wer ist „man“? Die elastische Energie in Form der elastischen Spannung. Aus der Sicht des Energie-Haushaltes ist es also ein „Ziel“, mit möglichst wenig aufgewendeter Riss-Energie möglichst viel Flächen-Spannung abzubauen. Ist der Riss erst einmal „gestartet“, pflanzt er sich in Richtung höchster Spannung fort, bis die Spannung nicht mehr ausreicht, weitere Rissenergie aufzubringen (am Rand des gesamten Mediums oder an dem eines Teilmediums, nämlich an einem anderen Riss, oder manchmal auch mitten drin, wie auf einem zugefrorenen Teich).
(In meiner Kristall-Sammlung befinden sich langprismatische Kochsalz-Kristalle mit mittiger Kerbe in der Basisfläche, die zu Riss-Ausbreitungs-Experimenten 1972 genutzt worden sind: Die Newtonschen „Ringe“ im Riss schillern durch den glasklaren Kristall. Das tun sie auch an inneren Rissflächen von Bergkristall sehr schön, die keine Verbindung zur Kristall-Oberfläche besitzen.)
Nun gibt es glücklicherweise zwei Zusammenhänge, die in die gleiche Richtung wirken:
A) Ist ein Riss einmal bei seiner Entstehung auf einen anderen „getroffen“, so wird an diesem „Abzweig“ die Spannung so gering sein, dass die Wahrscheinlichkeit, dass genau gegenüber ein neuer Riss entsteht, verschwindend klein ist. Das heißt im Umkehrschluss aber, dass es unwahrscheinlich ist, dass „Kreuzungen“ von Rissen entstehen. Es entstehen also wahrscheinlich nur Abzweige der Zahl Eins (eine einfache Kreuzung wäre ein Abzweig der Zahl Zwei, und höhere Kreuzungen wären gänzlich unwahrscheinlich – es sei denn, da liegt ein Stein im Schlamm…). Als „Zwickel“ zwischen drei Flächen hat der Abzweig im End-Bild natürlich die Zahl Drei, aber während der Bildung ist es die Zahl Eins der Abzweigungen, die uns philosophisch interessiert. Der Schlamm-Kobold muss also gar nicht bis Drei zählen können, um die Rissmuster zu machen! (Wenn man den Computer dreizählige Sterne statistisch um einen mittleren Abstand gestreut auf einer Fläche verteilen lässt und dann Verbindungslinien per Hand herstellt, so ergeben sich n-Ecke, deren mittlere Eckenzahl mit relativ geringer Streuung bei Sechs liegt.)
B) In der Fläche hat der Kreis das größtmögliche Verhältnis zwischen Rand und Flächeninhalt. Die geometrische Figur, die sowohl zur einheitlichen und vollständigen Parkettierung der Fläche geeignet ist (gleichseitiges Dreieck, Viereck und Sechseck) als auch dem Kreis am nächsten kommt, ist das Sechseck. Dieses ermöglicht also die günstigste Entlastung durch das beste Verhältnis von Fläche und Umfang. Und nun kommt’s: Die Zwickel zwischen den Sechsecken sind dreizählig! (Bei Vierecken sind sie vierzählig und bei Dreiecken sechszählig, was wir beides als unwahrscheinlich anzunehmen unter A) gelernt haben!)
Unser geschultes Auge hat zusammen mit unserem geschulten Verstand die komplizierteste Lösung anvisiert, nämlich die Zahl Sechs zu begründen. Dabei ist es so einfach, denn auch der Kreis ist einfach, weil der einfachste geometrische Ort im Zweidimensionalen: Konstanter Abstand zu einem gegebenen Punkt.
Nun wollte ich das Ganze natürlich auch modellieren. Und habe wie immer ganz einfach angefangen. ABER: Die triviale Statistik-Idee war blöd! Ich habe Zwickelpunkte statistisch auf eine Fläche verteilen lassen und anschließend Verbindungslinien zu den nächsten drei Nachbarn ziehen lassen und wollte die Eckenzahlen der entstehenden Vielecke statistisch auswerten. Hihi: Es entstehen dabei erstens natürlich auch viele Vielecke mit einigen konkaven Ecken, was dem Energie-Minimierungs-Prinzip nicht entspricht. Und zweitens entstehen entweder viele Zwickel mit mehr als drei Strahlen oder, wenn man das durch Bindungslängen-Einschränkung unterbindet, übrig bleibende Zwickelpunkte.
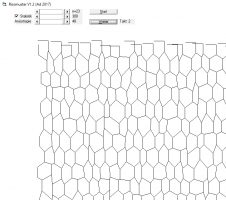
Die Versuche 1 (Bild 1) und 2 (übrige 3 Bilder mit Längenbeschränkung) zeigen, dass ein agenetisches Modellieren über Stochastik nicht zum Ziel führt, weil es nur ein Simulations-Versuch, aber keine wirkliche Modellierung ist.
(Aber auch Fehlversuche bringen Erkenntnisse und können bei guter Darlegung letzterer bei mir sogar als Diplomarbeit gelten!)
Die Genese ist wohl eher so: Die längste Ausdehnung einer Fläche wird durch eine leicht zickzackförmige „Mittellinie“ geteilt, die jeweils an einwärts liegenden Zacken der langen gegenüber liegenden Seiten beginnt. Es entstehen 2 Flächen. Jede dieser Flächen wird wieder auf gleiche Weise geteilt, wobei die beiden Startpunkte der auf „Mittellinie“ nicht identisch sein können, weil eine Zacke entweder in die eine oder in die andere Teilfläche zeigt. Setzt man diesen Prozess fort, so entstehen im Idealfall rechteckähnliche Flächen mit zwei Zusatzzwickeln auf im Mittel zwei der vier Seiten, so dass sie insgesamt von 6 Zwickeln (zwischen 4 und 8) eingefasst sind. (Sind es 7 statt 6, so fehlt dem Nachbarn einer und umgekehrt.)
Die auf diese Weise entstehenden „Sechsecke“ sind somit nicht automatisch gleichseitig, obwohl dies energetisch am günstigsten wäre, weil auf diese Weise die größte denkbare mittlere Nähe zum Kreis entstanden wäre (Kreis als ebene Figur mit dem kleinsten Verhältnis von Umfang zu Fläche).
In der Tendenz lässt sich aber folgern, dass eine Fortsetzung der Risse in die dritte Dimension genau in diese Richtung korrigiert werden würde: Statistisch sukzessive Anpassung an ideale Sechsecke! (Siehe die nächste Seite!)
Für die Modellierung bedeutet das folgendes:
- Festlegung einer Startsituation
- Rissbildung mit „Etappen“, die durch statistische Abweichungen von einer mittleren Teiletappenlänge bei statistischen Abweichungen von einem mittleren Zielwinkel (zwischen zwei in die Fläche ragenden Vorsprüngen) gekennzeichnet sind (als Variante auch von beiden Enden gleichzeitig ausgehend und sich in der Mitte treffen müssend)
- nächste Generation von Rissen bilden (fraktale Struktur!)
Problem ist die Datengrundlage: Objekte bilden oder Pixelabfrage (bmp als Datenbank? Siehe Erfahrung mit meiner ray-tracing-Variante…) oder hierarchische Indizierung mit entsprechend laufender Neuzuordnung? Letzteres wäre mir am sympathischsten.
Guter Plan für die Zukunft…
Übrigens: Bei einem „zweieinhalb-dimensionalen“ Problem (gewölbte Flächen!) ergeben sich neue Bilder, wie man auf gebrannten Glasuren (z.B. von Vasen, Tassen, Tellern) sehen kann:

Hauptrisse parallel und senkrecht

Hauptrisse nur teilweise parallel

kurios: ein Hauptriss ist sinusförmig
Schaut man genauer hin, findet man, dass Sattelpunkte anders aussehen als sphärisch oder zylindrisch gewölbte Stellen, und dass ein Torus offenbar etwas ganz Besonderes ist:

„Miro“-Tasse: wer malt kleine Dreiecke aus??

andere Ansicht

Konzentrische Startkreise im konkaven Teil, Satelliten-Kreise auf dem Torus-Teil

Übergang Mitte-Rand

Übergang Mitte-Rand

Torus-Satelliten im Detail
Diese Mischung von unterschiedlichen Krümmungen der Unterlage (in die sich die Risse NICHT fortsetzen können!) zeigt, wie eine Überlagerung von Stochastik und Gesetz zu „ästhetisch“ empfundenen Mustern mehrerer hierarchischer Ebenen führen kann.
Das legt die Frage nach der Genese nahe. Findet man vielleicht in einer Töpferei auch Objekte, wo Anfangszustände „eingefroren“ sind, weil die Spannungsenergie nicht ausreichte, die Risse zu bilden?
Da muss man nicht lange suchen:

Tasse 2 „unfertig“

Tasse 4 „unfertig“

Tasse 3 „unfertig“ (Untergrund offenbar noch unter Verwindungsspannung von der Töpferscheibe)

Vase 2 „unfertig“
Auch andere Materialien „machen“ ähnliche Muster bei ähnlich geformtem Untergrund:

Vase 3 mit anderer Glasur
Die zylindersymmetrisch konkaven Flächen auf dem Grunde einer Schale zeigen natürlich konzentrische Kreise, und wenn die „Innenhaut“ auch noch wellig unterlegt ist, sind primäre Kreismuster „vorprogrammiert“, die dann parallel verbunden werden (Vorrang für Rechtecke, also Vierecke statt Sechsecke):

Wellige Innenform einer Schüssel mit „Beeinflussung“ durch die Unterlage
Vorläufige Zusammenfassung der Beobachtungen:
Die Zahl 6 als näherungsweises Maximum einer „Eckenzahl“-Verteilung der Riss-Polygone ist NICHT ohne weiteres zu erkennen. Woran könnte das liegen?
Die weiter oben entwickelte Hypothese, dass je zwei „Vorsprünge“ auf gegenüberliegenden Viereckseiten die Startpunkte für neue Risse sind und damit im Mittel leicht doppelt abgefaste Vierecke zu Sechsecken werden, geht von einer relativ hohen elastischen Energie-Komponente aus. Ist diese geringer, wie zum Beispiel im trocknenden Schlamm, sind Viererzwickel „im Vorteil“ gegenüber Dreierzwickeln, weil an den im Dreidimensionalen bestehenden Kanten der „zweidimensionalen“ Zwickel der Trocknungsvorgang beschleunigt vorankommt: Jede zusätzliche Kante wirkt hier nun auf einmal strukturstabilisierend („positive Rückkopplung“).
Die These, dass mit der Tiefe der Vorzug von Sechsecken zunimmt, kann für Basalt (nächste Seite) gelten, aber eben nicht für dünne Glasurhäute auf Keramik. (Und deren Entstehung ist außerdem auf unterschiedliche Trocknungsverluste beim Brennen zwischen Glasur und Keramik selbst angewiesen – es gibt ja schließlich auch rissfreie Tassen – oder?)
Eine Modellierung müsste also alle diese Parameter als frei einstellbar enthalten – uff….
Fangen wir also wieder ganz einfach an, indem wir uns dumm stellen und mit Bleistift und Papier die einfachstmöglichen Situationen durchspielen.
Wir nehmen zwei Reihen von je zwei Viereck-Rissen als „Keime“ und lassen einige Zwickel sich ändern und verschieben und sehen nach, ob sich andere Vielecke bilden lassen, ganz ohne Lineal und Mathematik.

Hypothetische Ausgangssituation mit parallelen Rissen und den daraus folgenden „Vierer“-Zwickeln als „Keim“-Struktur
Gut, das geht wirklich. Es sind 1 Stück 5-Eck, 2 Stück 6-Eck und 1 Stück 7-Eck aus den 4 Stück 4-Eck im Inneren entstanden. Nun wollen wir es schrittweise ein wenig quantifizieren.
Wir nehmen nun fünf Reihen von je fünf Quadraten (da gibt es jetzt echte „Innere“) und verschieben zwei Reihen eine halbe Quadratseite. Auf diese Weise sind aus den 4-er-Zwickeln 3-er-Zwickel geworden. Jetzt lassen wir zu, dass die Zwickel sich zu regelmäßigen Sternen (3*120°) verformen, indem sie sich längs ihrer Symmetrieachse verschieben. Die Verbindungslinien bleiben Geraden. Aus einer ehemaligen Quadratseite der Verschiebungslinie wird somit ein Dach (oben und unten), die beiden anderen (rechts und links) werden lediglich verkürzt.

Verschiebung der Quadrate
Da sich weder die Zahl der Flächen noch die Gesamtfläche verändern, bleibt also die Fläche des entstehenden Sechsecks so groß wie die ehemalige Quadratfläche, und wir müssen uns „nur“ um die Länge der Umrandung kümmern, wenn wir das Verhältnis von Fläche und Umfang (das sollte bei der energetischen Betrachtung ja eine Rolle spielen, weil die längenproportionale Riss-Energie von der flächenproportionalen Verspannungsenergie aufzubringen ist) bewerten wollen. Wenn man der Einfachheit halber die Länge der Ausgangs-Quadrate auf 1 setzt, erhält man für die Sechseckseiten folgende Längen (Pythagoras und/oder Winkelfunktionen nutzen und selber nachrechnen!):

Verschiebung der Zwickel unter Beibehaltung der Fläche
Die Länge des Daches ist jetzt
2/Wu(3) = 1,155
und die Länge der verkürzten Seite
(1-1/(2*Wu(3)) = 0,711
Der Umfang ist somit von 4,000 auf 3,732 gesunken, also immerhin um 6,70%!
Ein regelmäßiges Sechseck der Fläche 1 für die komplette Parkettierung der Fläche mit der höchstmöglichen Symmetrie UND der geringstmöglichen spezifischen Rissenergie hätte einen Umfang von
6 * 1/3*Wu(2*Wu(3)) = 3,722
also nur um 0,25% besser (man erhielte es durch leichte Stauchung unserer länglichen Sechsecke, deren Mittelpunkte immer noch in den Mittelpunkten der ehemaligen Quadrate liegen, und die können nun einmal untereinander kein regelmäßiges -„gleichseitiges“- Dreieck bilden…)
Die Idealfigur mit minimalem Umfang bei gegebener Fläche, der für die Parkettierung allerdings ungeeignete Kreis, hätte bei der Fläche 1 einen Umfang von
2*Wu(Pi) = 3,545 (11,38% weniger als Quadrat)
Das heißt, mit unserem Bleistift-Papier-Test haben wir schon mehr als die Hälfte zum unmöglichen Idealfall und etwa 26/27 zum ideal möglichen Parkettierungsfall zurückgelegt!
Eine erste vorsichtige Modellierung, die den energetisch günstigsten Fall als „stabile Endsitutaion“ erreichen soll, müsste also mit einer deutlich nicht stabilen Anfangssituation starten (zum Beispiel eben mit den verschobenen Quadraten, die allerdings vom „realen“ Startfall nacheinander entstehender Risse immer noch meilenweit entfernt sind) und dann mit beweglichen Elementen (zum Beispiel mit gedämpften federähnlichen Interaktionselementen ohne Längenabhängigkeit der Federkraft, deren innere Energie damit ebenfalls nur linear längenabhängig ist) die „Rissenergie“ minimieren. Hört die Schwingung auf, ist die stabile Lage erreicht! Im ersten Test könnte man die „Sterne“ nur auf den Senkrechten bewegen lassen und müsste zu spiegelsymmetrischen Sechsecken kommen (aber wahrscheinlich mit Sternen, die keine dreizählige Rotationsachse haben!), bevor man alle Komponenten der Sterne freigibt und zu regelmäßigen Sechsecken kommt, wenn der Einfluss des Modellgebiet-Randes verschwindet (die Zahl der Zellen also wächst!).
So sieht der allererste Versuch in Version 1.0 aus:

Richtig. Es kommt genau das vermutete Muster heraus, da keine statistische Abweichung von der Symmetrie eingebaut ist.
Der Randeinfluss ist unterschiedlich zugelassen worden und gut sichtbar.
Nun sollte aber die Kernposition der Zellen statistisch bis zu einem Drittel Abstand schwanken können (Version 1.1):
Die Struktur wird relativ schnell glattgezogen, obwohl die Zugkräfte NICHT längenabhängig angesetzt worden sind!
Verändert man nun in der Version 1.2 auch die Streckung oder Stauchung der rechteckigen Mittelpunktverteilung (also die Anisotropie zwischen x- und y-Richtung), so werden wieder untereinander ähnliche Sechsecke entstehen, im Idealfall fast isometrische (regelmäßige):
Nun ja, die Ränder sehen noch komisch aus, aber im Inneren funktioniert es ziemlich gut.
Die Risse auf der Tasse haben offenbar keine Chance zum Ausgleich, weil die Glasur-Schicht sehr dünn im Vergleich zum Riss-Abstand ist. Das Thema „Ausgleich“ gehört also eigentlich in den nächsten Abschnitt, zum Basalt!! Dort pflanzen sich die Risse vom kalten Bereich in den abkühlenden warmen fort und können sich seitlich „bewegen“…
FAZIT bis hierher:
Am Anfang stand die Frage, ob Risse in einer Oberfläche zu bestimmten Strukturen neigen. Die Antwort ist eindeutig „JA“, wobei zu beachten ist, dass unterschiedliche Nebenbedingungen zu unterschiedlichen Mustern führen. Existiert ein Mechanismus, der zur Minimierung der Risslänge führen kann, sind Risse bevorzugt, die im Mittel 6-eckige Flächen einschließen.
NEBEN-ERKENNTNISSE
1.
Dynamisiert man ein hypothetisches stochastisches Anfangs-Rissmuster mit der Simulations-Idee von Kräften längs der Risse und lässt eine gebremste Beweglichkeit der Zwickel zu, um das energetisch wahrscheinlichste Muster zu erzeugen, so kommen diese Zwickel dort „zur Ruhe“, wo sich alle Kräfte aufheben. Das ist bei gleich großen Kräften dann der Fall, wenn der Zwickel regelmäßig ist, seine Strahlen also gleiche Winkel einschließen. Für den Dreier-Zwickel sind das 3 * 120°. Das bedeutet im Umkehrschluss, dass die Kraftkomponenten der beiden jeweiligen „Gegenspieler“ in Richtung des „Spielers“ zusammen so groß sein müssen wie die Kraft des „Spielers“ selbst, denn sonst gäbe es ja noch eine weitere Bewegung! Und weiter: Aus „Symmetrie-Gründen„, wie der Physiker sagt, sind sie untereinander gleich groß, also je halb so groß wie die des Spielers. Da bei gleich großen Kräften der Winkel 360°/3=120° ist (auch wieder aus Symmetriegründen!), so folgt ohne komplizierte Rechnung, dass bei 60° Abweichung von der Verlängerung der Spieler-Kraft die Gegenkraftkomponente der Gegenspieler halb so groß ist, und wenn man diese Aufteilung „Cosinus“ nennt, so ist cos(60°) = sin(30°) = 1/2. Und mit dem Pythagoras folgt dann für cos(30°) = sin(60°) = 1/2*√3. Damit haben wir neben den ganzzahligen rechtwinkligen Dreiecken 3-4-5, 5-12-13, 7-24-25 usw. ein weiteres leicht zu merkendes Dreieck gefunden.
2.
Man kann auch anders – jetzt wirklich völlig elementar – mit dem Dreier-Zwickel spielen, indem man einfach drei beliebige Punkte vorgibt und zwischen ihnen denjenigen Punkt sucht, dessen Verbindungslinien zu den gegebenen drei Punkten untereinander die Winkel 120° bilden. Das kann man mathematisch analytisch versuchen oder wieder „dynamisch“, nämlich durch eine echte „Modellierung„, was hier wie ein Suchprogramm aussieht, das den Verbindungslinien gleich große Kräfte zuschreibt und den Punkt so lange durch die resultierenden Kräfte verschieben lässt, bis er zur Ruhe kommt. Dann „müssten“ die Winkel alle 120° sein. (Man kann dem Punkt auch eine träge Masse zuweisen und die gebremste Bewegungskurve aufzeichnen… ) Der Vorteil dieser Modellierung ist, dass der gefundene Punkt nicht nur einfach eine analytische Lösung bezüglich diverser Bedingungen ist, sondern gleichzeitig als dynamisch „stabiles Gleichgewicht“ ausgemacht ist, weil ja jede Abweichung von ihm zu rücktreibenden Kräften geführt hat.
Start ist im blauen Punkt. Der rote Punkt schwingt zum Vergleich und zur Unterscheidung elastisch in den Schwerpunkt des Dreiecks, der grüne Punkt findet mit konstanten (im Betrag abstandsunabhängigen, aber auf die Eckpunkte gerichteten) Kräften den Winkel-Symmetrie-Stern-Punkt.
Übrigens: Wie sollte dieser Punkt in einem Dreieck heißen? Hat jemand einen Vorschlag?
Man merkt schon, dass es ihn nur in Dreiecken geben kann, deren stumpfester Winkel kleiner als 120° ist. In den anderen Fällen kreist der Grüne suchend auf der Ecke des stumpfen Winkels, wie man hier erkennen kann, denn aus dem Schwerpunkt (rot) kann man auf den unsichtbaren dritten schwarzen Dreiecks-Punkt schließen:

Schein-Lösung im unmöglichen Fall

Dreistern eingezeichnet

Stern und Dreieck eingezeichnet
Nun haben wir mit einer Stunde Programmier-Spaß (wie immer so elementar wie möglich in VB) auch noch nebenbei einen Satz der Technischen Mechanik (Statik) dynamisch visualisiert, nämlich dass im Schwerpunkt die Summe der Schwerkraft-Drehmomente Null ist: diese sind ebenso abstandsproportional wie die hier verwendeten Federkräfte!
(Die vier Ausgangspunkte sind zufällig generiert und die beiden Bewegungs-Endpunkte sind in 100 Schritten mit dem getakteten Newtonschen Gesetz – mit Dämpfung – numerisch integriert erreicht worden.)
Neuer Plan: Dynamik der Rissausbreitung modellieren (als Vorstufe zur energetischen Muster-Optimierung in die Basalt-Tiefe hinein)
Nun soll es also nach dem weiter oben schon erwähnten Plan passieren. Es ist spannend, ob das auch gelingen wird.
(in Arbeit…, bitte Geduld!)

















Kommentar abgeben