2.7.2.3 Gefüge mit zonierten Kristallen (Seigerung)
Jeder hat schon einmal zonierte Feldspat-Kristalle in einem Porphyr, Gneis oder Granit sehen können oder gar wirklich gesehen, denn diese liegen als Fußwegplatten oder als norddeutsche Kopfsteinpflaster ständig vor unseren Augen. Zuerst fallen die Feldspäte aber durch ihren Glanz auf, denn sie brechen gern in den bevorzugten Spaltebenen und bieten dem Auge dann – zufällig – den Brechungswinkel zum Sonnenlicht an. Das funktioniert, wenn die Bruchfläche – zufällig – in geringem Winkel zur Spaltebene steht, denn sie ist dann mikroskopisch als spiegelnde „Treppe“ ausgebildet (selbst wenn die Oberfläche, wie bei Kopfsteinen, makroskopisch leicht gewölbt ist). Eine geringe Änderung des Blickwinkels lässt den Glanz sofrt verschwinden. Gehen wir spazieren, ändern wir durch unsere Bewegung aber ständig die Winkel zu Pflasterstein und Sonne, so dass irgendwelche Steine ständig aufblitzende Feldspäte zeigen. (Diese heißen „Spat“, weil sie leicht spaltbar sind. Das ist in ähnlicher Form von den Geologen anderer Sprachen aus dem Deutschen übernommen worden.)
Die manchmal auftretende Zonierung unterscheidet sich von denen schöner Amethyst-Kristalle dadurch, dass sie nicht durch wechselnde Versorgung von außen, also unabhängig vom Wachstumsprozess im engeren Sinne, sondern von innen, also rückgekoppelt durch eine Verarmung der Restschmelze, herrührt.

Feldspatwechsel (gelber Plagioklas in der linken unteren Ecke des großen Kalifeldspats, der dunkle Entmischungsstreifen rechts zeigt) in einem einzigen Kristall-„Einsprengling“ (Osterzgebirge) (BILD zur Vergrößerung anklicken!)
Diesen Vorgang der „Seigerung“ (Konzentrationsänderung mit eventuell sichtbarer Schichtbildung während des Phasenübergangs) berechnet und veranschaulicht man am einfachsten in einer eindimensionalen Anordnung eines Zweistoffsystems, wie es beim Reinigungsverfahren der Zonenschmelze von Metallen oder bei der Destillation von Alkohol aus einem Alkohol-Wasser-Gemisch verwendet wird, was mathematisch keinen Unterschied ausmacht. Voraussetzung ist, dass zwei unterschiedliche Aggregatzustände des Gemischs im Gleichgewichtz bei einer gegebenen Temperatur unterschiedliche Zusammensetzung aufweisen. Im Temperatur-Konzentrations-Zustandsdiagramm zeigt sich das durch ein „augenförmiges“ und schräg stehendes Zwei-Phasen-Gebiet:
Hier könnte links der Alkohol und rechts das Wasser stehen. Man sieht, dass bei einer gegebenen Temperatur die beiden Phasen Dampf und Flüssigkeit eine unterscheidliche Konzentration aufweisen, und zwar mehr Alkohol im Dampf als in der Flüssigkeit. In grober Näherung kann man den Augenwinkel ganz links als zwei Geraden auffassen und daraus ein konstantes Verhältnis der Wasser-Konzentrationen im Alkohol flüssig/dampfförmig innerhalb eines kleinen Bereiches der Konzentration oder der Temperatur machen. (Dieser Wert heißt dann „Verteilungskoeffizient“.)
Würde man ein Wasser-Alkohol-Gemisch komplett durch den Destillationsapparat jagen, so hätte man danach die gleiche Mischung wie davor. Man muss also zum „richtigen“ Zeitpunkt aufhören. Wo dieser liegt, hängt von den Prioritäten ab: Will man viel wenig konzentrierten Alkohol oder wenig stark konzentrierten haben? Dann kann man überlegen, wie oft man das Ganze mit der entsprechend kleiner werdenden Teilmenge wiederholt oder ob man zur großtechnischen „fraktionierten Destillation“ übergeht, einem kontinuierlichen Verfahren in einer Destillations-„Kolonne“. (Bei der Zonenschmelze will man ebenfalls die „Verunreinigung“ weg haben, die sich am Ende in der Schmelz-Zone gesammelt hat, und verwirft diesen letzten Abschnitt nach dem Erstarren vor einem erneuten – eventuell gespiegelten? – Durchlauf.)
Mathematik-Einschub ähnlich der numerischen Integration:
Die mathematische Modellierung kann man wieder in EXCEL abwickeln, indem man den Prozess in lauter kleine Schritte zerlegt und diese nach der jeweiligen Korrektur-Rechnung aller beteilgten Elemente aneinander fügt.
Wir nutzen dieses Beispiel, um ganz grob zu untersuchen, welchen Fehler man bei starken Vereinfachungen macht. Deshalb fangen wir ganz primitiv an und wählen total einfache Zahlen für eine Kopfrechenübung. Wir wollen die Phase B reinigen, das heißt, Phase A verringern.
Kopfrechen-Überschlag 1:
Wir nehmen einen Fall an, wo Komponente A im Dampf (hier der Einfachheit halber konzentrationsunabhängig) halb so konzentriert vorliegt wie in der Flüssigkeit. Wir beginnen mit 3 Litern der Mischung 2 Liter B und 1 Liter A, also etwa 33% A in der flüssigen Mischung. Jetzt verdampfen wir 1 Liter und erhalten nach dem Kondensieren eine etwa 16%-ige Mischung, bestehend aus 160 ml A und 840 ml B. In den verbleibenden 2 Litern Ausgangsmischung müssen also noch 840 ml A sein, was jetzt 42% entspricht. Der zweite verdampfte Liter bringt ein 21%-iges Kondensat, gemischt mit dem ersten Liter ein Kondensat von 2 Litern 18,5%-ige Flüssigkeit. Den dritten Liter verdampfen wir NICHT mehr, weil sonst alles wieder wäre wie vor dem Start.
Kopfrechen-Überschlag 2:
Wir halbieren die Schrittweite und prüfen, was passiert. Der erste halbe Liter Kondensat ist wieder 16%-ig. Es fehlen nun 80 ml A, es sind also noch 920 ml in 2,5 Litern vorhanden, also 36,8%. Der nächste halbe Liter Kondensat von 18,4% enthält somit 92 ml A, was den Rest von 2 Litern auf 828 ml A, also 41,4%, schrumpfen lässt. Nun kommen 20,7% = 104 ml A herüber, macht zusammen einen Rest von 724 ml auf 1,5 Liter = 48 %. Im vierten und letzten Schritt (dann sind es zum Vergleich wieder 2 Liter Umsatz!) kommen 24%=120 ml herüber, was insgesamt zu 396 ml A in 2 Liter Kondensat, also 19,2 % geführt hat. Dieses Ergebnis ist schlechter als das im 1. Überschlag. Das muss auch so sein, weil wir ja so getan haben, als ob während des Verdampfen des ersten Liters nichts passiert. Wenn wir aber schrittweise zu einem kontinuierlichen Prozess übergehen (bei 1 Liter Dampfphase über der kochenden Mischung entspräche das bei Normaldruck etwa 1 ml Flüssigkeit, wäre also schon fast kontuinuierlich, wenn es von dort sofort zum Kondensieren in den Kühler geht), so verschlechtern sich die Bedingungen „während“ jedes Liter- oder Halb-Liter-Schrittes in Wirklichkeit schon stetig.
EXCEL-Überschlag mit 100, 1000 und 10.000 Schritten als Überschlag 3:
Es ergeben sich nach tabellarischer Rechnung in gleicher Schrittfolge wie oben 21,08% bei 100 Schritten und 21,13% bei 1000 Schritten und immer noch 21,13% bei 10.000 Schritten.
Diese Genauigkeit ist aber trügerisch, weil in Wirklichkeit die beiden Kurven für Taupunkt und Kochpunkt gekrümmt sind und somit einen konzentrationsabhängigen Verteilungskoeffizienten ergeben, wenn man ihn auf eine Phase allein bezieht. Für eine wirklich exakte Rechnung müsste man diese Kurven also analytisch beschreiben und in die Berechnung einbeziehen (oder tabellieren und mit der EXCEL-Tabellenverweisfunktion auslesen). Außerdem arbeitet man in der Praxis aus Zeitgründen nicht im Gleichgewicht der Phasen, was einen weiter verringerten Verteilungskoeffizienten ergibt. Dennoch haben wir gezeigt, dass das Gedankenexperiment grundsätzlich funktioniert!
Hier das EXCEL-Ergebnis, wenn man konzentrationsabhängig mit 100 Schritten numerisch arbeitet, den Kopf stetig kondensiert (und also aus dem Gleichgewicht herausnimmt) und langsam (also dem Gleichgewicht nah) destilliert: bei 2/3 Umsatz (wieder 2 von 3 Litern) liegt man dann nur bei etwa 24,5 %, also schlechter als im Kopfrechen-Überschlag oben. (Am Ende muss die Kopfkonzentration der Anfangskonzentration des Sumpfes entsprechen – das Diagramm endet aber bei 2/3 laut Aufgabe!)
Bei den „echten“ Gesteinsbestandteilen ist es natürlich viel komplizierter, weil mannigfach zusammengesetzt. Schon allein die Plagioklas-Reihe von NaAlSi3O8 zu CaAl2Si2O6 zeigt mehrere Zonierungsmöglichkeiten an:
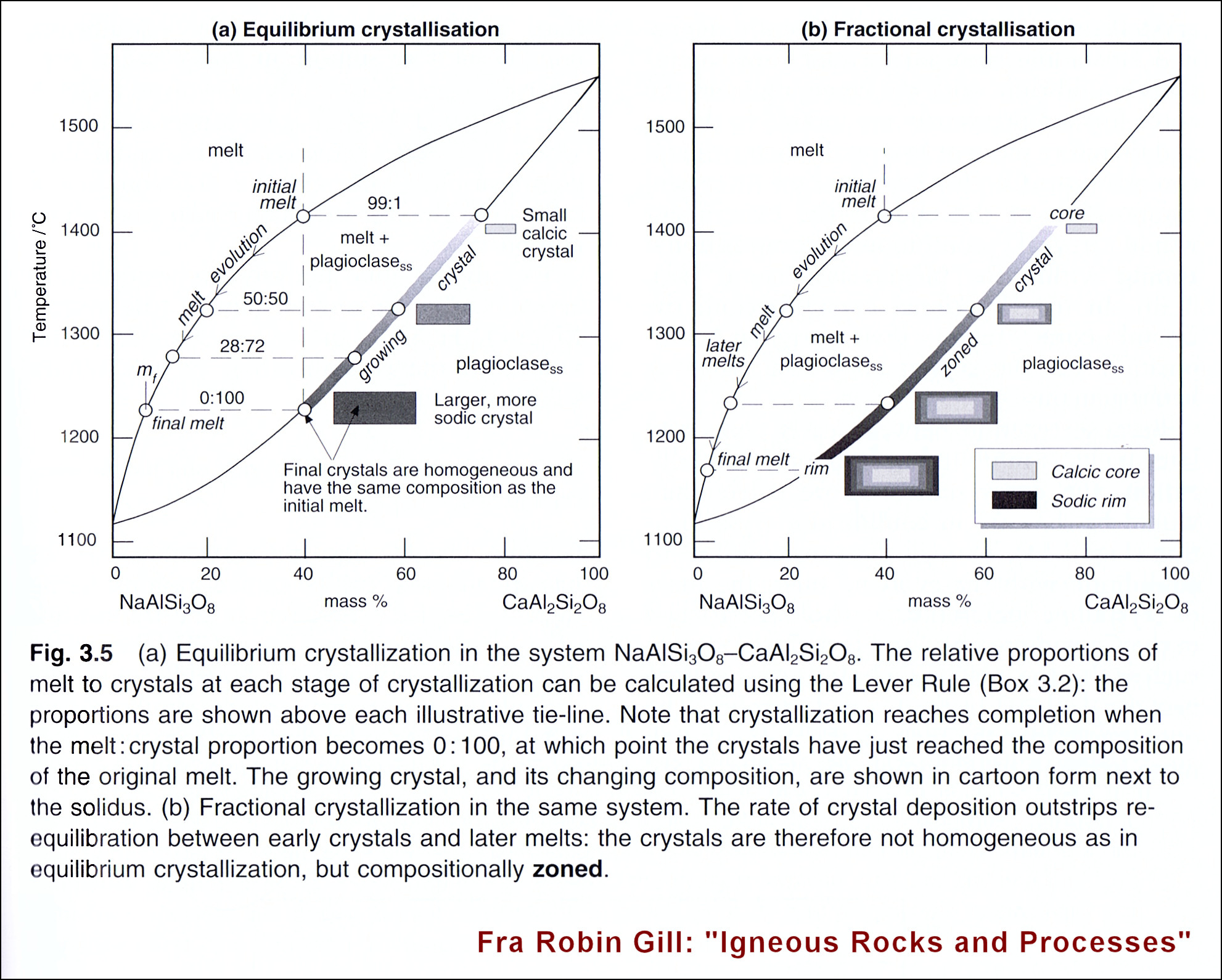
Vergleich von superlangsamem Wachsen mit ständigem Diffusions-Austausch zum Gleichgewicht im festen Zustand mit dem energetisch gehemmten Zonarwachstum

Dreieck der drei Feldspate mit Mischungslücke zwischen K und Ca, aber mehreren Phasen zwischen Na und Ca, die für die Zonierung gut sind. Bei Normaltemperaturen gibt es auch links eine Mischungslücke zwischen Orthoklas (K) und Albit (Na)! (Wiki)
Die Kali-Feldspäte haben nun Pech, weil eine Mischungslücke bei Normaltemperatur und Normaldruck dazu führt, dass sie in der festen Phase entmischen müssen und dünne Lamellen ausbilden (vergleiche nächstes Kapitel zum Eutektikum!), die manchmal farblich schwach zu erkennen sind. Das wird „perthitische Entmischung“ genannt.
Man erkennt wieder die begrenzte Reichweite der Lamellen. Oft stehen sie, anders als im Schema oben rechts, senkrecht zur langen Seite des Kristalls und sehen aus wie Risse (solche Risse aber gibt es ebenfalls, nämlich durch tektonische Einflüsse…). Das hat mit dem leichteren Eindringen der Wachstumsfront von der langen Seite her zu tun, auf der sie senkrecht stehen müssen (siehe nächstes Kapitel).













Kommentar abgeben