Extremwertaufgaben
Man kommt im Leben oft in die Situation, unter allen möglichen Varianten die Beste wählen zu wollen. In welchen Fällen kann dabei die einfache Mathematik helfen?
Aus der Beschäftigung mit der Differentialrechnung wissen wir, dass man den (lokalen oder manchmal auch globalen) Extremwert einer Funktion y(x) dadurch ermitteln kann, dass man eine Stelle sucht, wo deren Anstieg Null ist:
y'(x) = 0
Können wir also eine differnzierbare Funktion aus dem zu bearbeitenden Problem formulieren, so finden wir auf analytischem Wege die Lösung!
Beispiele
Beispiel 1: Technologisch und matarialeinsatzmäßig optimale Verpackung finden
Wir nehmen mal der Einfachheit halber eine zylindrische Verpackung an, deren Boden und Mantel aus dem gleichen Material bestehen und die als offene nahtlose Form hergestellt werden kann, und setzen einen Deckel drauf, der pro Flächeneinheit (z.B. cm²) den dreifachen Kosten-Aufwand erfordert wie der für den Rest. Wir geben zweitens ein Fassungsvolumen von 0,5 Litern vor. Welche Höhe und welchen Durchmesser hat das Gefäß dann im Falle optimaler (also minimaler) Kosten?
Oberfläche eines Zylinders:
Oz = Mantel + 2 * Boden = 2*pi*r*h + 2*pi*r²
Kosten als „gewichtete Oberfläche“:
Kz = Ko*(Mantel + 1*Boden + 3*Deckel) = Ko*2*pi*(r*h + 2*r²)
Es gibt zwei Variablen, nämlich r und h, die allerdings nicht unabhängig voneinander sind, wenn man sie über das gegebene Volumen V verknüpft (zweite Gleichung!!):
Vz = Boden * h = pi*r²*h
Damit gilt:
h = Vz/(pi*r²)
In die Kostengleichung eingesetzt:
Kz = Ko*(Mantel + 1*Boden + 3*Deckel) = Ko*2*pi*(r*Vz/(pi*r²) + 2*r²) = Ko*2*(Vz/r + 2*pi*r²)
Jetzt ist nur noch eine Variable übrig und wir können nach dieser differenzieren und Null setzen:
dKz/dr = Ko*2*(4*pi*r – Vz/r²) = 0
Daraus ergibt sich, dass die Klammer Null sein muss, und umgestellt nach r bedeutet das:
4*pi*r = Vz/r²
r³ = Vz/(4*pi)
und mit Vz = 500 cm³
r = (500cm³/(4*pi)) hoch (1/3) ) = 3,41 cm oder d = 2*r = 6,82 cm
h = Vz/(pi*r²) = 500 cm³/(pi*r²) = 13,7 cm
Probe: pi*r²*h = 500 cm³
Die gesuchte Verpackung ist also relativ schlank, was am teuren Deckel liegt.
Für einen nur doppelt (statt dreifach) teuren Deckel ergäben sich r = 3,76 cm und h = 11,3 cm und für gleiche Flächenkosten r = 4,30 cm und h = 8,60 cm, also Höhe gleich Durchmesser!

Kostenkurve als Funktion des Radiusses für diverse Aufschlags-Faktoren (Faktor 1, 2 und 3) für den Zylinder-Deckel bei gegebenem Zylinder-Volumen
Das ist gleichbedeutend mit dem Satz, dass der Zylinder mit quadratischem Querschnitt die geringste spezifische Oberfläche (als Quotient von Oberfläche und Volumen) oder das größtmögliche spezifische Volumen (pro Oberfläche) aller denkbaren Zylinder hat.
Und: Je aufwändiger der Deckel ist, desto teurer wird die Verpackung, selbst wenn sie dafür schmaler werden darf, aber eben länger werden muss.
Beispiel 2: Optimalen Winkel fürs Kugelstoßen finden
Beim Kugelstoßen kommen zum „normalen“ schrägen und reibungslosen Wurf aus der Schulmathematik noch mindestens zwei Aspekte hinzu:
- Armlänge
- Aufteilung des Energie-Aufwandes in kinetischen und potentiellen Anteil
Macht man das schrittweise, ergibt sich ein interessantes Diagramm:
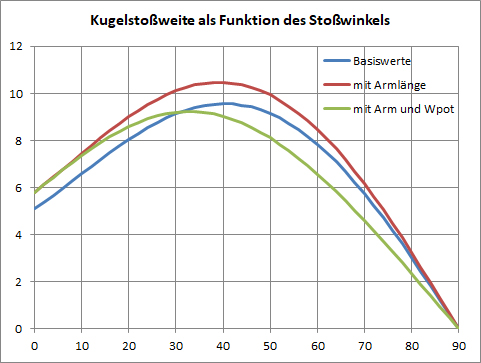
Schrittweise Annäherung an die Realität beim Kugelstoß: Der optimale Abstoßwinkel (Richtung der Armbewegung) liegt deutlich unter 45°!
Schon bei den so genannten „Basiswerten“ ist die Höhe des Abstoßes berücksichtigt (was man auch an der Weite von etwa 5 m beim Abstoßwinkel 0° erkennen kann) , weshalb auch hier schon ein optimaler Winkel unter 45° erscheint. Nimmt man die Armlänge hinzu, wird nochmals etwas auf die Weite (winkelabhängig!) aufgeschlagen. Und schließlich ist berücksichtigt worden, dass ein Teil der Armarbeit in das Anheben der Kugel inverstiert werden muss, wenn der Winkel mehr als 0° beträgt, was sowohl die Weite als auch den optimalen Winkel veringert. (Die Kurven sehen zwar wie Flugbahnen aus, sind aber NICHT solche, denn in der Abszisse steht der Abstoßwinkel und in der Ordinate die Stoßweite!!)
Die Berechnung erfolgte mit folgenden Zusammenhängen (quasi als EXCEL-Formeln wiedergegeben):
Berücksichtigung der potentiellen Energie durch Verminderung der Abstoßgeschwindigkeit vo auf voreal (Armlänge la und Abstoßwinkel beta bei Erdbeschleunigung g):
| voreal = Wurzel(vo²-2*g*la*sin(beta)) |
Berechnung der Flugzeit tb als Funktion von beta und der Abstoßhöhe h:
| tb(beta) = – v0real*sin(beta)/g + Wurzel(voreal²sin²(beta)/g² + 2*(h+la*sin(beta))/g) |
Berechnung der Flugweite der Kugel (ohne Luftwiderstand) aus der Flugzeit:
| sb = la*cos(beta) + v0real*cos(beta)*tb = (la + voreal*tb)*cos(beta) |
Schrittweise eingesetzt ließe sich daraus auch eine analytisch Lösung ermitteln, indem man wieder differenziert (nach beta) und Null setzt:
sb = (la + voreal*tb)*cos(beta)
Ersetzen von tb:
sb = (la + voreal*(- v0real*sin(beta)/g + Wurzel(voreal²sin²(beta)/g² + 2*(h+la*sin(beta))/g)))*cos(beta)
Ersetzen von voreal:
sb = (la + Wurzel(vo²-2*g*la*sin(beta))* (- Wurzel(vo²-2*g*la*sin(beta))*sin(beta)/g + Wurzel(voreal²sin²(beta)/g² + 2*(h+la*sin(beta))/g)))*cos(beta)
d(sb)/d(beta) = reine formale Fleiß- und Schreibaufgabe, Hilfe! (Kettenregel, Produktregel, …)
Beispiel 3: Optimale „Linie“ für den Abfahrtslauf finden
Bei Sportübertragungen im Winter hört man immer wieder, dass die richtige „Linie“ nicht gefunden worden ist oder dass plötzlich eine nicht für möglich gehaltene „noch bessere Linie“ gefunden worden sei.
3.1
Als erste gedankliche Vorübung sei eine Beschäftigung mit der Brachystochrone (Bahn kürzester Zeit für reibungsfreies Gleiten einer schweren Masse zwischen zwei gegebenen Punkten) empfohlen (z. B. Wiki). Man stößt dabei auf die Zykloide und erfährt, dass diese gleichzeitig eine Kurve ist, die eine vom Startpunkt UNABHÄNGIGE Zeit für das reibungsfreie Schwerkraft-Gleiten bis zum Tiefstpunkt ermöglicht (und somit Ausgangspunkt für eine Pendeluhr mit amplitudenunabhängiger Frequenz bildet).
Reibungsfrei ergibt sich durch numerische Integration für vier unterschiedliche Startpunkte tatsächlich, dass sich die vier gleichzeitig gestarteten Objekte zum Ziel (ganz unten) hin immer mehr annähern:
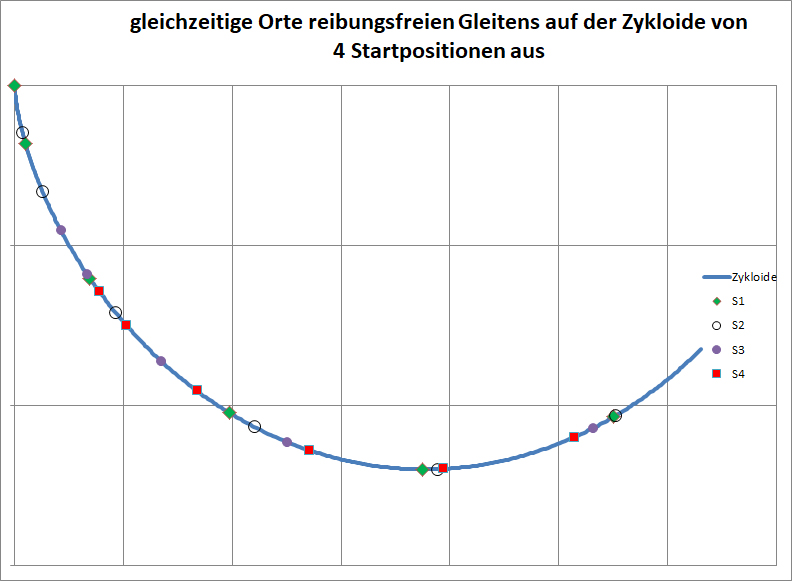
Mit den kleinen Abweichungen der numerischen Methode sieht man, dass sich alle reibungsfreien Gleiter trotz unterschiedlicher Startorte (aber bei gleicher Startzeit!) etwa im tiefsten Punkt treffen und dann umgekehrt gegenschwingen (Zeittakt für die einzelnen Spots jeweils gleich).
Fügt man nun variabel einstellbare (aber für alle Teilnehmer gleiche) geschwindigkeitsunabhängige Gleitreibung und geschwindigkeitsabhängige Luftreibung (Formfaktor und Exponent) ein, so kommt es erst NACH dem Tiefpunkt zur Vereinigung, sofern der Exponent größer als 1 ist.
Hier wurden als Gleitreibung konstant 0,1 und als Luftreibung 0,05 * v^2 eingestellt.
3.2
Die zweite gedankliche Vorbereitung sei die Untersuchung der Fahrzeit (Schwerkraft-Gleiten mit Widerstand: Berücksichtigung von sowohl Form-Faktor als auch Geschwindigkeits-Exponent) zwischen identischen Start- und Zielpunkten bei unterschiedlichem zweidimensionalem Profil.
Man erkennt, dass die Startneigung eine wesentliche Rolle spielt (wie man aus „echten“ Fernsehübertragungen weiß, wenn man die hektischen Doppelstockschübe bei flachen Startrampen einordnen kenn):
Die rote und die blaue Bahn (Parabel und Sinus in mehreren Parametern einer Geraden überlagerbar) haben zwar summarisch die gleichen Abweichungen von der Geraden, ihre Auswirkungen auf die Gleitzeit sind aber erheblich. Noch besser seiht man es, wenn man die grüne Bahn zur Geraden macht und dafür die Geschwindigkeitsexponenten der Reibung variiert (entspricht einer Veränderung des Verhältnisses von Gleitreibung der Ski und Luftwiderstand):
Je höher der Luftreibungsexponent der Geschwindigkeit ist, desto stärker werden steile (=schnelle!) Abschnitte bestraft, desto mehr ist die Gerade bevorteilt (sie ist außerdem kürzer!!) und kann den Startrampen-Nachteil ausgleichen. Blau verliert immer…
(Man kann nun natürlich auch noch Wind einrechnen, Reibungsunterschiede „oben“ (kalter Schnee am Start) und „unten“ (warm) zulassen usw. usf., je nach Zeit und Laune fürs Spielen.)
3.3
Hier nun endlich beim „realen“ dreidimensionalen Abfahrtslauf müssen wir selbst dann erst einmal vorsichtig schrittweise komplexer werden und also ganz einfach anfangen, wenn wir nur einen kleinen Streckenabschnitt betrachten wollen:
- Es ist ein 3D-Geländeprofil mit variablen Daten vorgegeben, für das es „seitliche“ Varianten gibt (im Gegensatz zur 2-dimensional freien Schwerkraft-Lösung durch die Zykloide)
- außerdem sind ein Start- und ein Zielpunkt festgelegt sowie eine Startgeschwindigkeit (Betrag und Richtung!) für jeden Streckenabschnitt (sonst hätten wir keine Vergleichsmöglichkeit)
- zusätzlich ist mindestens eine Geländemarke „außen“ zu umfahren (diese Randbedingung schränkt die Lösungsmöglichkeiten ein)
- die „Zielgeschwindigkeit“ (Betrag und Richtung!) im Streckenabschnitt sollte dann zusätzlich ein Kriterium für die Bewertung der Lösung sein, falls ein weiterer Streckenabschnitt folgen sollte
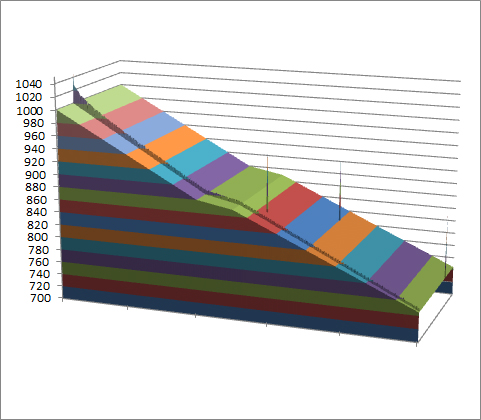
Skipiste mit 2 nicht umrundeten Torstangen und verfehltem Ziel bei numerisch integrierter beschleunigter Geradeausfahrt (niederiger Schatten sei hohe Geschwindigkeit)
Wir ahnen, dass es auf eine numerische Integration hinausläuft, bei der wir zu jedem Zeit- und also Raumpunkt schrittweise berücksichtigen können/müssen:
- Komponente der Hangabtriebskraft in aktueller Fahrt-Richtung
- Winkel zwischen Fahrt-Richtung und Ski-Richtung
- Luftwiderstand (als Funktion der Geschwindigkeit und der kurvenabhängig angenommenen Körperhaltung)
- Schneewiderstand als Funktion des Kurven-Radiusses UND der lokalen Geländekrümmung
Wir ahnen außerdem, dass es mit Sicherheit professionelle Programme für solche Probleme gibt und dass es außerdem Rennläufer geben wird, die durch die Selbstsicherheit aus lebenslangem Training auf solche Programme pfeifen…
Trotzdem ahnen wir, dass es viel Spaß machen könnte, sich schrittweise der Lösung zu nähern.
Zuerst müssen wir einmal die Bahnabschnitte beschreiben. Im obigen Bild wären das fünf:
1 erste Geradeaus-Fahrt zum beabsichtigten Kurvenbeginn um die erste Torstange
2 erste Kurvenfahrt um die erste Torstange bis zum richtigen Winkel in Richtung beabsichtigtem Kurvenbeginn um die zweite Torstange
3 zweite Geradeausfahrt bis zum beabsichtigten Beginn der nächsten Kurvenfahrt
4 zweite Kurvenfahrt bis zum richtigen Winkel für die Zielfahrt
5 dritte Geradeausfahrt zum Ziel
Bei gegebener Position der Torstangen (x,y) und gegebenem Hangprofil (z(x,y)) bleibt bei diesem Herangehen immer noch frei, wo der jeweilige Kurvenbeginn gesetzt werden soll und welchen Radius die Kurve haben soll. Das sind zusammen 4 Positionsdaten (x und y) und zwei Radien.
Schon die geometrische Berechnung der „gewollten“ Bahn in Koordinaten (x,y) ist nicht trivial. Die anschließende Berechnung der Geschwindigkeit auf dieser Bahn erfolgt sowieso numerisch integriert im konstanten Zeittakt, so dass man auch den Winkel mitführen kann und das Ende der jeweiligen Kurvenfahrt ohne vorherige Berechnung einfach durch Zielvergleich abfragen kann, wie das der Skifahrer ja auch mit dem Gesichtssinn macht (und nicht etwa auf die Uhr schaut oder auf die GPS-Koordinaten…).
Jetzt kann man schon Zeitmessungen machen und verschiedene Strecken-„Linien“ vergleichen, obwohl die Widerstände noch nicht eingebaut worden sind, lediglich die Hangabtriebskraft und die Streckenlänge gehen ein. Es kommen „Werte“ zwischen 37 und 39 „Sekunden“ für die reichlich 500 m heraus. (Man erkennt, dass an den Schnittstellen offenbar noch Übergabeprobleme existieren und die indirekte Geschwindigkeitsdarstellung dort klappert.)
Das ist alles sehr mühsam und wenig anschaulich.
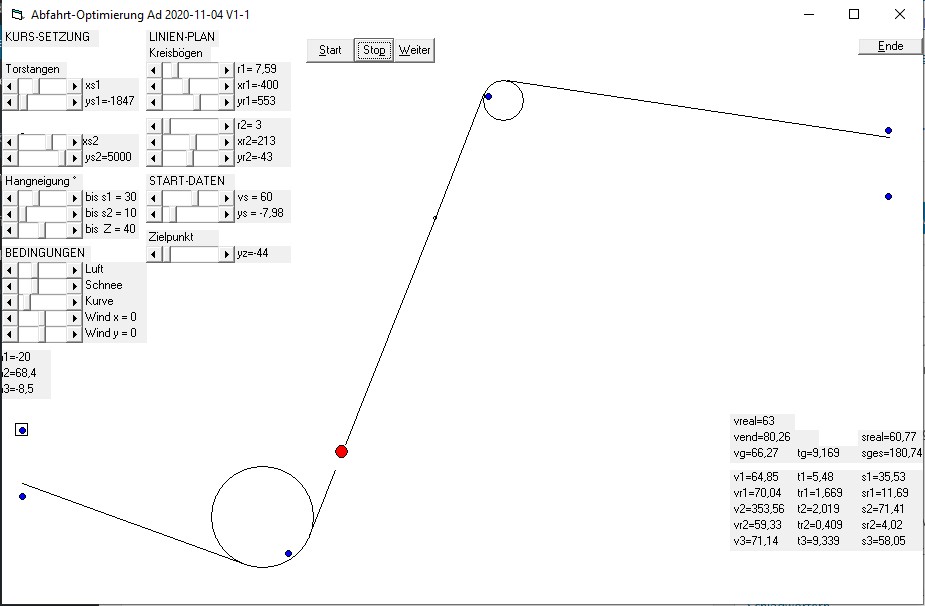
Besser wäre eine echte Modellierung, visualisiert im Zeittakt, also ein VB-Modell zum Beispiel:
Zuerst wird die Strecke „gesteckt“, dann für den hier abgebildeten und berechneten Abschnitt der Gesamtstrecke ein „Linien-Plan“ gemacht und dann die Fahrt unter Beachtung sämtlicher Anfangs- und Randbedingungen integriert. Man kann dem roten Punkt bei seiner Bewegung zusehen und alle Momentan- und Summenwerte verfolgen.
Schnell wird klar, dass das Ganze hochkomplex ist:
- Ziel muss es sein, ein Optimum für die beiden Werte Abschnitts-Zeit und End-Geschwindigkeit zu bestimmen, was widersprüchlich sein kann (außer, wenn es der letzte Abschnitt ist), denn was nutzt eine geringe Zeit auf Kosten einer langsamen Weiterfahrt?
- Je nach Schnee-Qualität und Wind können sowohl die Radiuswahl als auch der Punkt des Schwung-Ansatzes (trotz modernster Ski-Kanten-Form und angepasster Ski-Elastizität) wichtig sein
- Das gleiche gilt fürs Streckenprofil, besonders bezüglich der Hangneigung in einer so genannten „Traverse“ (wer denkt hier an die legendäre „Streif“?), also einer Querfahrt zwischen zwei Toren.
Schon allein eine veränderte Anfangsgeschwindigkeit in diesem Streckenabschnitt bringt ein anderes Optimum der Linie mit sich, was nur bestätigt, wie weit sich Fehler von „weiter oben“ „fortpflanzen“ können. Das gleiche gilt für Durchfahrtspunkt (nah an der Stange?) und Winkel der Durchfahrt.
Skiwachsqualität und windschlüpfrige Fahrtposition sind hier als integrierte Größen in „Luft“, „Schnee“ und „Kurve“ enthalten und also für die gesamte Strecke konstant. Die Zwangskräfte, die vom nicht elastischen (!!) Schnee aufgenommen werden müssen (sowohl radius- und geschwindigkeitsabhängig bei Kurvenfahrt als auch – deutlich geringer – bei Schrägfahrt zur Falllinie), kosten also kinetische Energie, genauso wie die Kombination von Fahrtwind und Wind. Energie-Quelle ist allein die Hangabtriebskraft.
Am Ende begreift man bei diesem Spiel, dass im echten Schnee wohl ohne fleißiges Üben nichts zu gewinnen ist, denn man muss unterwegs als „Regler“ schnell entscheiden können, wie die geplante „Linie“ gehalten werden soll, ohne dass man erst einmal in Ruhe eine Kontrollrechnung durchführen kann. Interessant wäre der Vergleich zwischen professionellen Ski-Renn-Läufern und Robotern auf gleichem Material, denn ganz nebenbei muss man auch noch das Gleichgewicht halten…
Ich kann mit Hilfe meiner Modellierung bestätigen, dass das manchmal nervende Gerede von Reportern, Trainern und Sportlern über scheinbare Kleinigkeiten einer Weltcup-Fahrt nicht an den Haaren herbeigezogen, sondern die psychologisch gefärbte Umschreibung reinster Physik ist!
Wie programmiert man das?
Als äußere Kräfte wirken die Hangabtriebskraft (nur die Komponente in der Zwangsrichtung: Strecke hier der Einfachheit halber in drei geradlinige – s1, s2, s3 – und zwei kreisbogenförmige – sr1, sr2 – Abschnitte mit Übergängen ohne Knick zerlegt, was schon für sich eine gute analytisch-geometrische Übung ist) und der Fahrtwind (komplett nur in der Zwangsrichtung) sowie die Windwirkung (wieder auf die Fahrtrichtung bezogen) und die unelastischen Zwangskräfte (leichtes Rutschen bei Schrägfahrt zum Hang und vor allem bei Kurvenfahrt). Hierzu sind Material- und Formkonstanten anzusetzen, die man im Modell durch Eingaben ändern kann.
Es bleibt nicht aus, dass man dabei Trugschlüssen erliegt. Zum Beispiel beim Kurvenfahren:
Nimmt man nur einfach die Radialbeschleunigung v²/r als Auslöser, so integriert sich deren Wirkung proportional zum Kurvenwinkel, so dass es völlig unwesentlich ist, welchen „engen Radius“ man wählt. Aus der Praxis weiß man aber, dass es nicht so ist: Eine enge Kurve bremst bei gleichem Winkel viel mehr als eine weite. Ursache ist das nicht-Kraft-proportionale Verhalten von Ski UND Schnee. Mit einer Zusatz-Potenz der Krümmung (reziprokem Radius) und einem entsprechendem konstantem Ausgleichs-Umrechnungs-Faktor erhält man realitätsnahe Ergebnisse. Also: Auch physikalisch lernt man hinzu, wenn man modelliert und mit der Realität vergleicht!
Selber essen macht fett, also bitte nachmachen!
Kraft -> Beschleunigung -> Geschwindigkeit -> Weg, alles im Zeittakt.
(Die Idee eines Weg-Taktes kollidiert leider mit der Programmier-Erfahrung des nicht proportional eintellbaren Timer-Intervalls, was für einen „echten“ Zeitablauf erforderlich wäre, auch wenn die Integrale trotzdem stimmen würden.)









Kommentar abgeben