2.4.0 Grundkurs Diskretisierung: Sandhaufen
Kann man schrittweise lernen, wie man eine Diskretisierung erfolgreich durchführt? Ob dazu das Schütten eines Sandhaufens ein gutes Beispiel ist, wenn es darum geht, eine entstehende geometrische Form zu ermitteln? Ich weiß es selber noch nicht, bin genauso gespannt wie der Leser!
Wir wollen WIRKLICH in ganz kleinen Schritten vorgehen:
A) 1-dimensional
1. Ein einziges Sandkorn (kugelförmig) fällt senkrecht auf eine Fläche (elastisch oder teilelastisch)
2. Zwei Körner fallen dicht hintereinander (auch untereinander elastisch oder teilelastisch)
3. Viele Körner fallen senkrecht auf denselben Punkt
B) 2-dimensional
4. Viele Körner fallen statistisch verteilt auf nahe beieinander liegende Punkte
5. Die Körner weichen statistisch etwas von der Kugelform ab
6. Die Körner haben statistisch leicht verteilte Größen
Wie immer, wenn man etwas modellieren will (modellieren so verstanden, dass man nicht bestimmte feststehende Dinge grafisch darstellen will, sondern lediglich Grundgesetze verwendet und nicht geschlossen analytisch darstellbare Vorgänge durch schrittweise Berechnung (siehe „numerische Integration!“) zusammensetzt.
Zuerst muss man sich klar werden, welche Hilfsmittel man benutzen will. Im Grunde genügen Papier und Bleistift, wenn man SEEEHR viel Zeit hat. Werkzeuge wie Tabellenkalkulation oder Programmiersprachen sind sehr hilfreich, wenn man sie zu nutzen weiß.
IMMER ist es ERSTENS sinnvoll, die ersten Schritte entweder mit Papier und Bleistift oder mit EXCEl zu prüfen, ob sie prozedural überhaupt zu einem sinnvollen Ergebnis führen können. Und ZWEITENS sollte man von vornherein nur eine schrittweise Steigerung der Komplexität planen und jeden Schritt auf plausible Funktionalität prüfen (das vereinfacht die Fehlersuch enorm!!!)
Also nun:
1. Ein einzelnes kugelförmiges Sandkorn fällt senkrecht auf eine ebene Fläche
Wir haben eine Start-Höhe, eine Beschleunigung nach unten (Schwerkraft) und bei einem Kontakt mit der Fläche ein Reflexion, bei der Energie verloren gehen kann. Man kann das alles als Zeitablauf eines gefärbten Kreises entlang der Senkrechten programmieren (z.B. Visual Basic) oder eine Tabelle der Höhe als Funktion der Zeit erstellen (EXCEL) oder eben schrittweise auf Papier rechnen.
Dazu teilen wir die Zeit in kleine Intervalle ein und rechnen je Intervall die Änderung der Geschwindigkeit (durch die Erdbeschleunigung) aus und damit den je Intervall zurückgelegten Weg. Da es uns nur ums Prinzip geht, können wir runden, die Erdbeschleunigung g z.B. auf -10 m/s², das Sandkorn auf 1 mm Radius. Wenn wir den „Ort“ des Sandkorns als den seines Mittelpunkts verstehen wollen, geht es so los, wenn wir je 100-stel Sekunde rechnen wollen (t in s, h in m, Start z.B. in 10 m):
Start: t=0 -> h=10
Erster Zeit-Schritt:
t=0,01 -> dv = dt*g = 0,01 * (-10) = -0,1 ->
v(neu) = v(alt) + dv = 0 – 0,1 = -0,1
dh=v(mittel)*dt=(0 – 0,1)/2*0,01=-0,0005
h(neu)=h(alt)+dh = 10 – 0,0005 = 9,9995
Fertig!
Das machen wir nun immer weiter. Dabei ahnen wir schon, dass v gleichmäßig wachsen muss, wenn g konstant ist und jeder Schritt 0,01 s dauert. Die Höhe nimmt dann also mit einer quadratischen Funktion ab, wir erhalten die erwartete Parabel im Höhe-Zeit-Diagramm.
(Das hat schon Galilei mit seinen Wasserstrahl-Versuchen so gemacht, dass er den Zeitablauf durch die horizontale Bewegung in x-Richtung ersetzt hat, indem er den Strahl schräg nach oben richtete… Beide Diagramme – h(t) und h(x) – müssen also gleich aussehen, wenn man die Luftreibung – geht beim Strahl mühelos! – vernachlässigt.)
Und richtig, das Rechenergebnis sieht als Diagramm so aus:

Höhenabnahme mit der Zeit bis zum Aufprall am Boden für ein einzelnes Sandkorn ohne Luftreibung
(Man kann mit der in der Schule gelernten Formel nachprüfen, ob die Zeit von 1,4 s (exakt wäre es Wurzel(2)) richtig sein kann.)
Aber jetzt wird es spannend, denn die Reflexion am Boden ist zwar anschaulich völlig klar, programmtechnisch aber schwierig. Warum?
Es wäre ja blanker Zufall (und von diesem dürfen wir beim Programmieren NICHT abhängig sein!!!!), dass der Aufprall genau am Ende eines Zeitintervalls stattfände und das Programm so „schlau“ wäre, das genau zu erkennen. Der WORST CASE wäre in Wirklichkeit, dass wir bei der Abfrage der Höhe (erforderlich für die Entscheidung, ob die Richtung umgekehrt werden müsse) das Kriterium „negativ“ nehmen, aber bei gleichzeitiger nicht vollkommen elastischer Reflexion gar nicht in positive Höhe zurückkommen und also ewig unter Null mit ständig wechselndem Geschwindigkeitsvorzeichen herumzittern… Und selbst bei völliger Elastizität ist der Umkehr-Ort ja nicht zufällig bei jeder Sprung-Periode derselbe, sodass eine völlg periodische Kurve gar nicht zustande kommen kann (wir wissen ja, das Wurzel(2) irrational ist und nicht durch einen endlichen Bruch dargestellt werden kann).
Man kann sich nur helfen, indem man für die Berechnung der reflektierten Geschwindigkeit den Algorithmus ändert, indem man für die Ermittlung der neuen Werte entweder zwei Zeitabschnitte zurückgeht oder einfach den letzten Wegschritt (also immer ins Positive) umkehrt. Das ergibt einen kleinen Fehler, aber der ist proportional zur Größe des Stützstellenabstands auf der Zeitachse und also direkt beeinflussbar. (Probiert das selber aus, in EXCEL fängt man das mit einer WENN-Funktion ab, in der der Zellbezug steht, in Basic mit der IF-Abfrage und entsprechender Neuberechnung, falls man nicht die vorherigen Werte vorsorglich in Zwischenspeicher abgelegt hat).
Dann erhält man eine fehlerfreie gedämpfte Reflexion, hier in EXCEL als Diagramm:

Gedämpft springendes Korn mit 90% Elastizität
Bei stärkerer Dämpfung am Boden (für eine technische Schüttung wohl angebracht) könnte sich auch das ergeben:

Hier kommt das Korn schnell zu Ruhe
Die „Ruhe“ des Korns ist der endlichen Strichdicke geschuldet, man könnte im Programm auch einen Schwellwert einbauen, unterhalb dessen sich das Korn nicht mehr bewegt. (Das schränkte aber weitere Freiheiten beim späteren Behandeln eines Haufens ein, wie zum Beispiel ein Nachrutschen in unteren Schichten…)
Die strenge Prüfung, ob es jetzt klappt, ist die Elastizität 100%, denn dann sollte die Anfangshöhe exakt erreicht werden:

Test bestanden, bei der Bodenelastizität Eb=1 geht keine Energie verloren, die Sprunghöhe bleibt konstant
Die Sprung-Dauer ist nun noch etwas ungenau, weil ja die rechnerische Reflexion erst unter der Reflexionsebene stattfindet, aber das wird die Suche nach der Haufen-Form nicht wesentlich beeinflussen… (7,5 Halb-Perioden mal Wu(2) ist wirklich knapp 10!) Der Fehler würde übrigens bei Rechnung mit kleinerem Zeitintervall („Stützstellen-Abstand„) ebenfalls kleiner werden.
Fazit: Mit einem einzelnen Korn haben wir erst einmal einen funktionierenden Ansatz für die Darstellung der Bewegung gefunden.
2. Zwei identische kugelförmige Sandkörner fallen senkrecht nacheinander auf eine ebene Fläche und stoßen sich gegenseitig
Nun brauchen wir einen Radius der Körner und einen Zeitabstand beim Fallen. Auch das lässt sich in EXCEL noch leicht aufbauen. Zuerst testen wir den Zeitabstand ohne Wechselwirkung der Körner untereinander:

2 Körner hüpfen unabhängig voneinander, aber zeitversetzt
Nun führen wir endlich eine Wechselwirkung beider Körner mit einer zweiten Elastizität Ek ein (der nichtelastische Teil trägt zur Erwärmung der Körner bei, sofern sie nicht zerbrechen, was aber keine Rolle für ihre Bewegung spielen soll). Für den teilelastischen Stoß nutzen wir die Zwischen-Transformation ins Schwerpunktsystem und teilen dann proportional die Impulse mit verringerten Geschwindigkeiten auf (wieder mit der Wurzel der Elastizität, die ja die Energie – im SP-System! – verringert, in der die Geschwindigkeit quadratisch steckt). Das führt zu einer zweiten Abfrage, ähnlich der zur Bodenberührung: jetzt zur Unterschreitung des Mindest-Abstands von 2 Radien. (Man sieht, schon dieser kleine Schritt zum 2-Körper-System birgt sehr viele Fehlermöglichkeiten, weshalb ja alles wirklich in Einzelschritten komplettiert werden muss!!!)
Jetzt stoßen sich beide Körner mit viel Energieverlust (80% Verlust der kinetischen Energie):

Komisches Ende, wenn sich beide „fangen“, weil die hier gewählte Abfrage zulässt, dass die Schwerkraft „umgangen“ wird – der fehlerhafte Ablaufplan muss überarbeitet werden!

Veränderte Stoß-Elastizität Ek („Kollision“) untereinander, Eb („Boden“) gleich
Aber auch das „Reflektieren“ beim ersten und den weiteren Zusammentreffen befriedigt unser „Gefühl“ nicht. Woran kann das liegen? Ich habe lange gebraucht, um meinen Irrtum aufzudecken:
Erstens ist unser Unbewusstes schneller als unser Denken, es sucht in der Erfahrung nach ähnlichen Vorgängen und findet eine Diskrepanz zwischen Erwartung und Realität. Aber was ist die Realität? Das Diagramm? Nicht vergessen: Die Horizontale ist die Zeitachse! Ist sie wirklich mit der x-Achse einer 2D-Bewegung zu vertauschen?
Zweitens: Sind wir sicher, alle Symmetrien gedanklich verarbeitet und geprüft zu haben?
Symmetrien sind mehrfach vorhanden:
- gleicher Radius beider Stoßpartner
- gleiche Masse beider Stoßpartner
- deshalb gleicher Betrag der Differenz beider Stoßpartner zur Schwerpunktgeschwindigkeit sowohl vor als auch nach dem Stoß
- im vollkommen elastischen Fall (bei Reflexion am Boden und untereinander) sind außerdem die Geschwindigkeiten, bezogen auf den Boden, beim Stoß immer gleich, weil sie sich aus der potentiellen Energie über dem Boden ergeben, und beim Stoß sind beide (fast!) gleich weit vom Boden entfernt, falls (!) ihr Radius sehr klein ist
Aber jetzt kommt’s:
Im allgemeinen 2D-Fall (und natürlich auch 3D-Fall!) werden die Geschwindigkeitskomponenten zweier gleichschwerer Partner beim elastischen Stoß senkrecht zur (durch die Schwerpunktbewegung gebenen) Symmetrielinie reflektiert, die parallel zu dieser Linie liegenden Komponenten bleiben erhalten. In unserem Diagramm sind aber keine zwei Komponenten vorhanden, weil es keine geometrische 2D-Darstellung ist, sondern hier ein 1D-Fall über die zusätzliche grafische Zeitachse nur wie ein 2D-Fall aussieht. Durch Verluste bei der teilelastischen Reflexion veränderte Geschwindigkeiten entstehen also trügerische Winkel in der Darstellung, die eine verkorkste Reflexion vorgaukeln…
Wir testen das gleich mit dem einfachsten Testprinzip, nämlich mit extremalen Werten: OHNE Energieverlust (Eb=Ek=1), also vollkommene Elastizität:
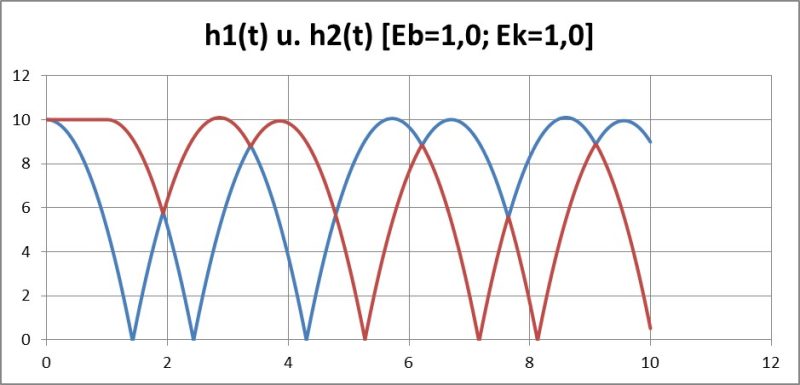
Vollkommen elastische Reflexionen sehen aus, als ob die Kugeln im Fluge nur die Farben gewechselt hätten

Jetzt stoßen die Kugel untereinander mit Verlust, aber elastisch am Boden, die „Scheinbahnen mit Farbwechsel“ erscheinen leicht geknickt

Jetzt dämpfen sie sich gegenseitig noch mehr („fangen“ sich am Ende gar als Artefakt des schlechten algorithmischen Abfangens), die Knicke sind deutlicher zu sehen!

Hier dämpft nur der Boden, aber die Körner reflektieren gut aneinander, was man wieder am „knickfreien Farbwechsel“ sehen kann (allerdings etwas parallel verschoben wegen endlichem Kugelradius!).
Puh. So kann man auf die unerwartete Wirkung eigener Darstellungs-Ideen am Anfang hereinfallen, und dann durch Nachdenken und systematisches Testen alles wieder einrenken!
LEHRE: Man darf nicht gleich aufgeben, wenn einem etwas unverständlich erscheint. AUS FEHLERN KANN MAN WUNDERBAR LERNEN!!!
(Geht bald weiter, heute ist der 24.12.2022.)
Kommentar abgeben