2.3 Muster aus Konvektionszellen
Frage:
Kann man heuristisch herleiten, welche Struktur in einer Schicht mit thermischer Konvektion am wahrscheinlichsten ist?
Die Frage klingt viel einfacher, als sie ist.
In einer Kaffetasse kann man das manchmal beobachten: Die noch nicht gleichmäßig verteilte Sahne zeigt Zellenbildung an, weil am Rand und an der Oberfläche abgekühlter Kaffe nach unten sinken „will“ und dafür heißer nach oben steigen „muss“ (oder umgekehrt formulierbar, wirklich!).
(Bei Wikipedia ist unter „Rayleigh-Bénard-Konvektion“ stattdessen Goldfarbe in Aceton genommen worden, bitte Filmchen dort ansehen und an Kaffee erinnern!)
Der instinktive erste Gedanke ist, dass „wie immer“ Sechsecke entstehen müssen.
Der „nachgedachte“ zweite Gedanke widerspricht dem, weil er einwirft: Worin soll eigentlich der Unterschied zwischen Aufsteigen und Absinken bestehen, wenn wir bei einem inkomprssiblen Medium Masse-Erhaltung und Symmetrieprinzipien haben?
Im Detail bedeutet dieser Einwurf, dass die Struktur NICHT zwischen Aufsteigen und Absinken unterscheiden darf, und dass deshalb die Zahl der Nachbarn der Aufstiegs-Zellen gleich der der Abstiegszellen sein soll, und zwar sowohl in Hinsicht auf „gleiche“ wie auf „ungleiche“ Nachbarn. Es geht also um eine vertauschbare Parkettierung in zwei Farben!
Das geht natürlich streng genommen nur mit Quadraten! Jedes aufsteigende grenzt an vier absteigende und umgekehrt. Und jede Zelle ist „nur über Eck“ mit vier gleichartigen „verbunden“. Mit Dreiecken und Sechsecken will uns eine gleichberechtigte Parkettierung nicht gelingen, ohne irgendwelche „Überstrukturen“ heranziehen zu müssen oder es gelingt, wenn wir auf Gleichheit der Elemente verzichten.
Das Bild, das wir an der Oberfläche einer Zelle sehen, verführt uns aber zu anderen Annahmen: Dort ist eine breit gewölbte Fläche zu sehen, wo sich der aufsteigende Flüssigkeitsstrom nach allen Seiten hin verteilt und dann in den „Zellgrenzen“ wieder nach unten verschwindet. Die Querschnitts-Fläche dieser Grenzen erscheint uns viel kleiner als die des aufsteigenden Stroms. Das würde aber bedeuten, dass die Geschwindigkeit des Abstiegs viel höher wäre als die des Aufstiegs, was ziemlich unwahrscheinlich sein dürfte. Trotzdem werden uns aber überall solche Kombinationen von sechseckiger Draufsicht und symmetrisch paralleler Seitenansicht (Querschnitts-Skizzen) gleichberechtigter Ströme nahegelegt, ohne den Widerspruch zu bemerken, der zwischen beiden Darstellungen offenbar besteht?
Es besteht offensichtlich viel mehr Klärungsbedarf als angenommen!
Erinnerung: Wirbel. Es bestehen ja offenbar (Heuristik!) geschlossene Bahnen, also Wirbel. Gegenstrom benachbarter Wirbel an ihrer Berührungsfläche wäre reibungstechnisch „irgendwie blöd“. Also Ringwirbel-Wirbelringe. Da gäbe es keinen Gegenstrom an den Grenzen. Aber was machen wir mit den Zwickeln zwischen den „auf Lücke“ (also doch sechseckig??) angeordneten Ringen?
Übrigens: Reibungstechnisch und trägheitstechnisch gibt es sicher ein energetisches Minimum in Abhängigkeit vom Verhältnis zwischen der Höhe der Konvektionszelle und ihrem Durchmesser. Man sollte dann bei der Draufsicht auf solche Ereignisse auf die Dicke der Schicht schließen können!
Aber zurück zur Struktur. Stellen wir uns also blöd und bauen ein Sechseck-Muster auf, bei dem die Fläche des Aufstroms (innen in grünen Sechsecken) gleich der Fläche des Abstroms (dazwischen, also um die roten Hilfs-Linien herum) ist:

Ein Grundmuster roter Sechsecke wird durch „innere“ grüne Sechsecke ergänzt, deren Flächeninhalt gleich dem verbleibenden Rand sein soll. Die grünen Abmessungen sind somit 1/2*Wurzel(2) (also 0,71) von den roten.
Aber eigentlich wollten wir Aufstrom und Abstrom gleich behandeln, nicht nur flächenmäßig, sondern auch nach ihren Konturen? Sollten wir da die Zwickel nicht zu Sechsecken aufweiten?

Aber nun sind die Reste der inneren grünen Sechsecke kleiner geworden. Was nun? Da wir einfach davon ausgehen, dass sich die Strukturen irgendwie von selber „abrunden“ werden, müssen die konvexen Strukturen noch weiter schrumpfen und die konkaven wachsen, was die Flächengleichheit zerstört. Also vergrößern wir erst die grünen Bereiche uns lassen dann rote Sechsecke als „Zwickel“ vor dem Abrunden zu, dann sind nur noch konvexe Formen da:

Die grünen „Rest-Sechsecke“ sind nun noch regelmäßig, die roten „Zwickel-Sechsecke“ aber nicht, dafür aber flächengleich. (Wer Spaß daran hat, kann ja mal rechnen, wie groß die grünen Ausgangs-Sechsecke sein müssen, damit das verbleibende regelmäßige Aufstrom-Seitenmitten-Sechseck die gleiche Fläche wie das unregelmäßige Abstrom-Sechseck dreizähliger Rotationssymmetrie hat!)
Wenn wir aber wieder die innere Reibung der Flüssigkeit hinzudenken, nützt gleiche Querschnittsfläche auch nichts, da ein Rechteck eine höhere innere Reibung (bei gleichem Durchsatz) als ein Quadrat (bei gleicher Fläche) hat. Entstanden sind also bis jetzt abgerundete regelmäßige Sechsecke mit einem Kranz aus je sechs abgerundeten unregelmäßigen Sechsecken, also ein ziemlich runder „Kern“ für die eine Strömungsrichtung und ein geriefter „Schalen“-Schlauch drumherum für die andere Richtung, der gleichzeitig auch gültig für die benachbarten sechs Kerne ist.
Wir merken also: Wir können uns drehen und wenden wie wir wollen, es gibt keine Lösung, die alle Bedingungen gleichzeitig erfüllt: Wir sind wieder einmal im Dimensionskonflikt gelandet! Man erkennt das leicht beim Beobachten der „echten“ Konvektionszellen: Sie sind nur kurzzeitig stabil, weil sehr empfindlich gegen Fluktuationen. Das macht zum einen die Voraussage von Gewittern sehr schwierig und führt zum anderen in der Verfahrenstechnik dazu, dass man Flüssigkeiten lieber zusätzlich rührt, als sich ganz auf die Konvektion zu verlassen. Aber „ungefähr gleich groß“ und „ungefähr auf Lücke“ erscheinen die Konvektionszellen dann doch und erinnern an die Statistik der Riss-Muster mit im Mittel ähnlich großen sechseckigen Elementen der Gesamt-Struktur.
Übrigens:
Wir haben bei unseren Betrachtungen außer Acht gelassen, das etwas unseren Wunsch nach völliger Symmetrie prinzipiell durchbricht: Die gerichtete Schwerkraft, die Auslöser der Zellen ist, ist gleichzeitig auch Zerstörer der Symmetrie, denn es gibt „oben“ eine andere Phasengrenze als „unten“: Flüssigkeit-Gas und Flüssigkeit-Festkörper. Oben gibt es ein „Aufwallen“ („Schwerewellen“) am Ende des Aufstroms um das Zentrum der Zelle, unten aber nichts Vergleichbares. Das damit zusammenhängende, radiale „Nach-außen-Strömen“ gibt den Drehsinn des Ringwirbels vor und also den Sachverhalt, dass der Aufstrom als „Kanal“ ausgebildet ist und der Abstrom als „Schlauch mit Längsriefen“ zwischen den abgerundeten Zwickeln. (Es wäre ein schönes Experiment zur „Stabilität“ der Struktur, zwischen die bestehenden Aufstrom-Kerne einige Abstrom-Kerne zu pflanzen und zuzusehen, wie diese sich auflösen oder in Aufstrom-Kerne wandeln. Das Wandern der „gerieften Schläuche“ und die Teilungs- und Vereinigungsvorgänge von Zellen sprechen da Bände… Denn grundsätzlich kann man ja die Schläuche längs aufreißen lassen, so dass sich die benachbarten Kerne umgekehrt zu Schläuchen vereinigen…)
Für die im Zeitmittel „stabil“ erscheinende Struktur einzeln labiler Strukturelemente „mittlerer“ (also trotz allem optimaler) Größe gibt es offensichtlich zwei Gründe:
- Zu große (das heißt flache) Zellen zerfallen in zwei Teile. Der radiale Gipfelstrom „schafft es nicht“ bis zum Abstromschlauch – dieser bildet einen Abzweig quer durch die Zelle. (Vergleiche Riss-Muster!) Halbquantitative Beschreibung: Ein „Strudel“ destabilsiert die Zellwand!
- Zu kleine (das heißt zu lange) Zellen sind stark strudelempfindlich und brechen zugunsten benachbarter größerer Zellen zusammen, das heißt, der Strudel biegt sich nach oben (oder unten) um und vereint sich mit der radialen Gipfelströmung.
Ein singulärer Aufstrom allerdings (z. B. heiße Explosionswolke) senkt sich dann in Pilzform wieder ab, wie auch ein singulärer Abstrom (Kalt-„Tropfen“ von Luft in der Atmosphäre oder von Flüssigkeit in einem Behälter oder Meer) als umgekehrter Pilz wieder nach oben wallt!
Fazit:
Ja, man kann fast ohne zu rechnen zu den wahrscheinlichen Strukturen der Konvektionszellen kommen, wenn man schrittweise vorgeht! Und man kann gleichzeitig erkennen, dass solche Strukturen sehr störanfällig sind!
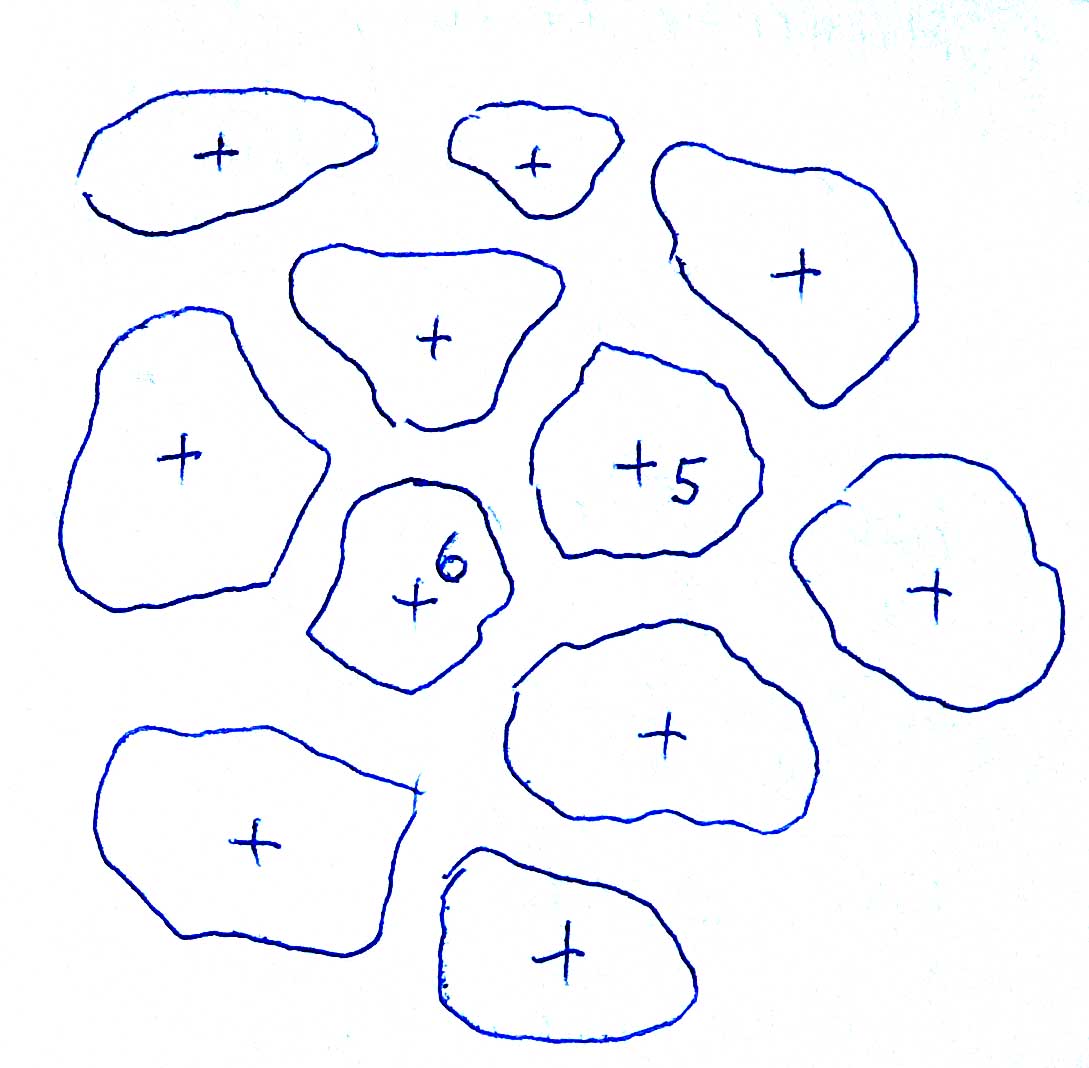
Flüchtige Handskizze nach den obigen Erkenntnissen: Es entstehen mehr oder weniger abgerundete und sich bewegende (pulsierende, sich vereinigende oder trennende) Aufstrom-Zellen mit 5 oder 6 (oder auch 7) Nachbarn und gemeinsamen Abstrom-Bereichen. Die letzteren sehen „in der Natur“ oftmals viel schmaler aus, was wahrscheinlich am Oberflächenhäutchen der Flüssigkeit liegt, das sich in den Abstromschläuchen zusammenschieben lässt (auch das ist gut auf Kaffeetassen zu sehen, wenn das Häutchen durch vorsichtiges Gießen der Kaffeesahne noch durchsichtig geblieben ist!!).
Ausblick mit Aufblick:
Überlagert man die Konvektion mit seitlicher Strömung, wie das beim Wetter oft „gemacht“ wird, gibt es zusätzlich „liegende“ gerade Wirbel, die in der Wolkenschicht oft schön zu sehen sind. Ihre Vermischung mit den zellularen Strukturen macht das System dann blitz- und donnerartig richtig „fett“.

http://www.wetter-foto.de/foto-65466-erster-blitz-2013.html
Kommentar abgeben