2.8.1.2 Perihel-Drehung des Merkur
Kann man die Perihel-Drehung des Merkurs nachvollziehen?
Aus der Literatur weiß man, dass die Periheldrehung des Merkurs drei Ursachen hat:
1. Die Abplattung der Sonne zu einem Rotationsellipsoid führt zu einer Vorwärtsdrehung der Apsidenlinie.
2. Der Einfluss von Venus, Jupiter und Erde (in dieser Reihenfolge, aber auch der der anderen – alle außerhalb der Merkurbahn befindlichen – Planeten) führt zu einer Vorwärtsdrehung der Apsidenlinie.
3. Der Einfluss der Zentralmasse auf die Raumzeitkrümmung führt zu einer Vorwärtsdrehung der Apsidenlinie.
(Die erste Ursache ist im gesamten Komplex 2.8 behandelt, ausführlich unter 2.8.3.2. Daraus folgt, dass JEDE – auch rotationssymmetrische! – Abweichung vom Kugelpotential im Schwerefeld zu einer Apsidendrehung führt. Also: Selbst ein auf einer Kreisbahn „gleichmäßig verschmierter“ Jupiter würde die Ellipsen der anderen Planeten drehen, allerdings rosettenartig strukturiert statt „chaotisch“, wie hier gleich gezeigt werden wird.)
Die zweite Ursache soll hier dargelegt werden.
(Die dritte Ursache ist in ihrer modellierten Darstellung noch in Arbeit, ist aber schon allein aus dem Spiel mit dem Exponenten des Kraftgesetzes plausibel, das eine Veränderung der Potentialform generell ermöglicht. Da jede konkrete Potentialform als Reihenentwicklung der durchgespielten theoretischen darstellbar ist, sind keine spielfremden Effekte zu erwarten.)
Zuerst ein einfacher Vergleich zum Verständnis von potentieller Energie, kinetischer Energie und Zeitbedarf:
Bahnen gleichen Start- und gleichen Zielortes in einem Kraftfeld unterscheiden sich trotz gleicher Energiebilanz in den „verbrauchten“ Zeiten wegen ihrer Unterschiede in der mittleren kinetischen Energie (wegen der Unterschiede in der mittleren potentiellen Energie!) UND wegen der unterschiedlichen Weglänge voneinander. Mit Hilfe der Variationsrechnung kann man im Falle der Zulassung von Zwangskräften eine optimale Trajektorie berechnen. Noch einfacher ist der Vergleich zweier paralleler gerader Radwege, deren einer eben ist und deren anderer durch eine flache cosinusförmige Mulde führt. Vom Gefühl her neigen wir „vorausschauend“ dazu, die ebene Route zu wählen, um den Anstieg am Ende zu umgehen. Aber die Mulde ist der schnellere Weg, solange sie nicht zu tief ist und solange die Luftreibung nicht wesentlich ist, weil am Anfeng ein Geschwindigkeitsgewinn steht und am Ende erst ein Verlust auf den ursprünglichen Wert erfolgt! (Wir setzen einmmal stillschweigend voraus, dass unsere eingestellte Tretleistung den mittleren Luftwiderstand ausgleicht.)
Die Lösung für die schnellste Bahn im konstanten ebenen Feld ist die Zykloide (siehe Beispiel 3.1 unter „Extremwertaufgaben„).
Was hat das mit Merkur und Venus oder Jupiter zu tun?
Der Merkur erfährt jedesmal beim (inneren!) Überholen des äußeren Planeten erst eine Beschleunigung noch vorne und außen (resultierend eine Erhöhung seiner Bahngeschwindigkeit trotz Bahn-„Erhöhung“) und dann eine nach hinten und außen (Verringerung seiner Bahngeschwindigkeit). Das wird in Opposition wieder zeimlich ausgeglichen. ABER: Da die Merkur-Bahn an sich schon elliptisch ist und die Zentralmasse im Brennpunkt steht, ist im Aphel des Merkurs der Abstand zum äußeren Planeten kleiner als im Perihel, weshalb dort der Einfluss des Jupiters noch etwas stärker ist. Man kann es sich also so vorstellen, dass der äußere planet das Merkur-Aphel „nach vorn“ zieht, was zu einer Vorwärtsdrehung der Apsidenlinie des Merkurs führt.
UND: Da die Umlaufzeiten beider Planeten kein einfaches ganzzahliges („rationales“) Verhältnis bilden, ist keine übergeordnete „einfach ästhetische“ Schwebungs-Struktur zu erwarten, wie das auch schon beim Doppelpendel (siehe ganz unten als Anhang) nicht zu erwarten ist. Obwohl der Prozess voll determiniert ist, wirkt er also „chaotisch“. (Das ist der Grund, warum die „Periheldrehung des Merkur“ stets als Mittelwert über mindestens 100 Erdenjahre angegeben wird!)
Die folgenden Bilder zeigen meine „qualitative“ Modellierung (also nicht mit den Originalwerten!) nach Newton:

Zur Erinnerung: Strukturierte Apsiden-Links-Drehung („Rosette“) durch flachen Zentralkörper-Ellispoid
„Jupiter“ (oder „Venus“) macht hier je 2,2 Umläufe für etwa 10 des „Merkurs“. Je nach Startposition dreht die Merkur-Ellipse unterschiedlich chaotisch nach links (Ausgangsrichtung der großen Halbachse waagerecht).
(Die Berechnung erfolgte in 50.000 EXCEL-Zeilen ohne VBA. Schon bei einer Verringerung auf nur 10.000 Zeilen tritt im Falle des Rechteckverfahrens der numerischen Integration der Artefakt einer leichten Spiralbahn des Jupiters zutage!)
(Der Einbau des klassischen Jupiter- oder Venuseinflusses auf den Merkur in ein spielerisches Gesamtprogramm – erstes Bild der obigen Serie – zusammen mit dem Ellipsoid-Einfluss der Sonne soll in den nächsten Tagen erfolgen.)
Man kann auch eine Perihel-Drehung bei einer „Verschmierung“ des äußeren Planeten zu einem „Ring“ erkennen, wie die folgende Modellierung zeigt (hier mit einem Viertel der Zentralmasse im fünffachen Abstand):
Wie man sieht, fehlt jetzt das „chaotische“ Element, es entsteht eine regelmäßige Rosette durch die Störung des kugelsymmetrischen Feldes (Verzerrung durch einen ebenen Anteil, was qualitativ die gleiche Wirkung wie eine Raumkrümmung hat).
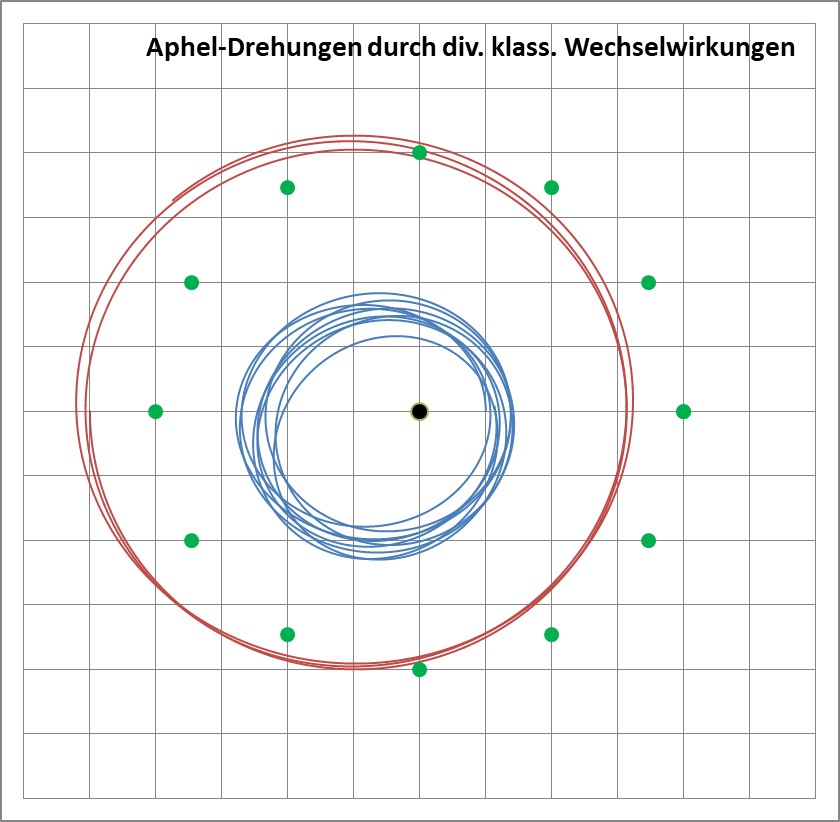
Eine Überlagerung von innerem oder äußerem „Ring“ (grüne Punkte) und äußerem Planeten (rote Bahn) ergibt eine Mischung beider Effekte:
Der „Chaos-Charakter“ wird dann noch klarer, wenn die „blaue“ Probemasse (Start rechts bei y=0) größer wird und auf den „roten“ Außenplaneten (Start links bei y=0) in gleicher vorwärtsdrehender Weise zurückwirkt (rot und grün haben hier untereinander keine WW!):
Heuristisch aber ist schon jetzt so viel klar:
Eine Vorwärtsdrehung der Ellipse zur Rosette erfolgt immer durch ein relativ zum 1/r-Potential steileren Potentialverlauf durch eine Position des „virtuellen Schwerezentrums“ (VSZ) zwischen Symmetriezentrum und Probemasse, wie das beim
- flachen Rotations-Ellipsoid (virtuelles Kraftzentrum liegt weiter außen als der im Koordinaten-Ursprung liegende Schwerpunkt)
- spielerisch erhöhten negativen Kraftexponenten (und also auch Potentialexponenten)
- außen liegenden Ring (Die mit wachsendem Abstand wachsende Anziehungskraft nach außen zum Ring verringert zunehmend die nach innen zum Zentrum zeigende und führt damit auch zu einem steileren Potential! Dieser Außen-„Ring“ kann über einen genügend großen Zeitraum hinweg auch durch eine dort kreisende zweite Probemasse ersetzt werden, wie bei den Planeten außerhalb des Merkurs.)
- relativistisch relevanten Masse-Abstands-Verhältnis („zusätzliche“ Raumzeitkrümmung zur verursachenden Masse hin erhöht die Zentralkraft)
der Fall ist. (Liegt das VSZ allerdings jenseits des Symmetriezentrums – was in der gravitativen Natur sehr selten vorkommt, denn es setzt eine verstärkte Masseverteilung längs der Rotationsachse wie beim elektrischen Zylinderpotential voraus -, ergibt sich eine Rückwärtsdrehung der Apsidenlinie der Ellipse. In JEDEM Fall des Auseinanderfallens von Symmetriezentrum und VSZ liegt also eine asynchrone Schwingung im rotierenden Bezugssystem zwischen radialer und tangentialer Bewegung vor.)
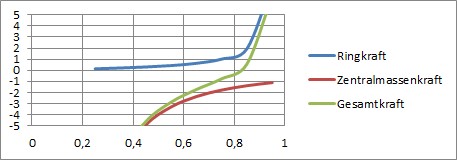
Schematisch sieht das bei der Überlagerung des Kraftverlaufs von klassischer Zentralmasse und Außenring so aus (grüne Kurve mit übertriebener blauer Ringkraft, vgl. auch die ausführliche Herleitung des „Ring-Feldes“ in 2.8.3):
ANHANG:
Vergleich mit dem Doppelpendel als „determiniertem Chaoten“
Hier eine numerische Integration der Bewegung eines Doppelpendels (beide Längen gleich, obere Masse fünfmal die untere, siehe auch ausführlicher unter 2.8.6.1):
Auch hier ist also (je nach Anfangsbedingungen) eine zwar chaotisch aussehende, aber dennoch determinierte Bewegung zu sehen. Eine „Struktur“ als geometrisches Muster wäre erst als „Einhüllende“ nach sehr vielen Bewegungen zu sehen, so wie auch die Merkurbahn dann eine „Einhüllende“ hätte.