Numerische Integration
Kann oder will man eine Differentialgleichung nicht geschlossen (analytisch) integrieren, so bleibt der Weg des Fleißes: Zu jedem Punkt (meist Zeitpunkt, untereinander durch einen bestimmten Betrag – Stützstellenabstand – als „Stützstellen“ für die Berechnung getrennt) bestimmt man den Wert derjenigen Größe A, die die Veränderung von B hervorruft, berechnet die durch sie hervorgerufene Veränderung von B und addiert diese zum vorherigen Wert von B.
Der dabei auftretende Fehler wird um so kleiner, je kleiner der Stützstellenabstand ist. (In der Schule hat man das mit rechteckigen oder trapezförmigen Streifen unter den Funktionen gemacht.)
Drei Beispiele sollen das illustrieren, und zwar solche, die uns allen aus verschiedenen Gründen geläufig sind: Geld und Bewegung. (Die Bewegung kennen wir aus dem Alltag seit dem Säuglingsalter, denn Tastsinn und Gesichtssinn wurden allmählich kombiniert und ergaben ein Raum- und ein Zeitempfinden. Und mit Geld haben wir leider auch immerzu zu tun.)
Beispiel 1:
Der Geldfluss Fp auf mein Konto und der von ihm weg (Fm) sollen durch folgende hypothetisch stetige Funktionen gegeben sein:
Fp = a*t + b (a=4 €/Monat²: Überweisungsänderung von der Oma, b=1000€/Monat vom Arbeitgeber)
Fm = -c (c=1100€/Monat: Überweisungen an Lieferanten)
Wieviel Geld habe ich nach 60 Monaten auf dem Konto, wenn es am Anfang leer war und es keine Zinsen gibt?
Wir können natürlich beide Gleichungen zusammenfassen:
F = a*t+(b-c) und über die Zeit zum Geldstand G integrieren:
G = G(0) + a/2*t² + (b-c)*t
und ausrechnen für t=60 Monate:
G = 0€ + 4/2*3.600€ – 100*60€ = 7.200€-6.000€ =1.200€
Machen wir das mit einer Tabelle, geht das so:
Monat 1: 0€ + 4€ + 1.000€ – 1.100 € = -96 €
Monat 2: -96€ + 8€ + 1.000€ – 1.100€ = -188 €
Monat 3: -188€ + 12€ + 1.000€ – 1.100€ = -276 €
…
Monat 60: 1.180€ + 240€ + 1.000€ -1.100€ = 1.320€
Hier die komplette Tabelle:
| Geld auf meinem Konto | |||||
| Oma | 4 | €/Monat² | |||
| AG | 1000 | €/Monat | |||
| Ausgaben | 1100 | €/Monat | |||
| Monat | Oma+ | AG+ | Ausgaben- | Fluss | Stand |
| 1 | 4 | 1000 | -1100 | -96 | -96 |
| 2 | 8 | 1000 | -1100 | -92 | -188 |
| 3 | 12 | 1000 | -1100 | -88 | -276 |
| 4 | 16 | 1000 | -1100 | -84 | -360 |
| 5 | 20 | 1000 | -1100 | -80 | -440 |
| 6 | 24 | 1000 | -1100 | -76 | -516 |
| 7 | 28 | 1000 | -1100 | -72 | -588 |
| 8 | 32 | 1000 | -1100 | -68 | -656 |
| 9 | 36 | 1000 | -1100 | -64 | -720 |
| 10 | 40 | 1000 | -1100 | -60 | -780 |
| 11 | 44 | 1000 | -1100 | -56 | -836 |
| 12 | 48 | 1000 | -1100 | -52 | -888 |
| 13 | 52 | 1000 | -1100 | -48 | -936 |
| 14 | 56 | 1000 | -1100 | -44 | -980 |
| 15 | 60 | 1000 | -1100 | -40 | -1020 |
| 16 | 64 | 1000 | -1100 | -36 | -1056 |
| 17 | 68 | 1000 | -1100 | -32 | -1088 |
| 18 | 72 | 1000 | -1100 | -28 | -1116 |
| 19 | 76 | 1000 | -1100 | -24 | -1140 |
| 20 | 80 | 1000 | -1100 | -20 | -1160 |
| 21 | 84 | 1000 | -1100 | -16 | -1176 |
| 22 | 88 | 1000 | -1100 | -12 | -1188 |
| 23 | 92 | 1000 | -1100 | -8 | -1196 |
| 24 | 96 | 1000 | -1100 | -4 | -1200 |
| 25 | 100 | 1000 | -1100 | 0 | -1200 |
| 26 | 104 | 1000 | -1100 | 4 | -1196 |
| 27 | 108 | 1000 | -1100 | 8 | -1188 |
| 28 | 112 | 1000 | -1100 | 12 | -1176 |
| 29 | 116 | 1000 | -1100 | 16 | -1160 |
| 30 | 120 | 1000 | -1100 | 20 | -1140 |
| 31 | 124 | 1000 | -1100 | 24 | -1116 |
| 32 | 128 | 1000 | -1100 | 28 | -1088 |
| 33 | 132 | 1000 | -1100 | 32 | -1056 |
| 34 | 136 | 1000 | -1100 | 36 | -1020 |
| 35 | 140 | 1000 | -1100 | 40 | -980 |
| 36 | 144 | 1000 | -1100 | 44 | -936 |
| 37 | 148 | 1000 | -1100 | 48 | -888 |
| 38 | 152 | 1000 | -1100 | 52 | -836 |
| 39 | 156 | 1000 | -1100 | 56 | -780 |
| 40 | 160 | 1000 | -1100 | 60 | -720 |
| 41 | 164 | 1000 | -1100 | 64 | -656 |
| 42 | 168 | 1000 | -1100 | 68 | -588 |
| 43 | 172 | 1000 | -1100 | 72 | -516 |
| 44 | 176 | 1000 | -1100 | 76 | -440 |
| 45 | 180 | 1000 | -1100 | 80 | -360 |
| 46 | 184 | 1000 | -1100 | 84 | -276 |
| 47 | 188 | 1000 | -1100 | 88 | -188 |
| 48 | 192 | 1000 | -1100 | 92 | -96 |
| 49 | 196 | 1000 | -1100 | 96 | 0 |
| 50 | 200 | 1000 | -1100 | 100 | 100 |
| 51 | 204 | 1000 | -1100 | 104 | 204 |
| 52 | 208 | 1000 | -1100 | 108 | 312 |
| 53 | 212 | 1000 | -1100 | 112 | 424 |
| 54 | 216 | 1000 | -1100 | 116 | 540 |
| 55 | 220 | 1000 | -1100 | 120 | 660 |
| 56 | 224 | 1000 | -1100 | 124 | 784 |
| 57 | 228 | 1000 | -1100 | 128 | 912 |
| 58 | 232 | 1000 | -1100 | 132 | 1044 |
| 59 | 236 | 1000 | -1100 | 136 | 1180 |
| 60 | 240 | 1000 | -1100 | 140 | 1320 |
Verflixt, woher kommt der Unterschied von 120€ bei deiden Rechnungen?
Der Grund ist einfach, aber für den Anfänger schwer zu verstehen:
Bei der (stetigen) Integration einer (stetigen) Funktion ändern sich die Werte von Sekunde zu Sekunde oder Tausendstelsekunde zu Tausendstelsekunde oder…, bei der diskrete Rechnung aber nur einmal im Monat. Bei 60 Monaten mit je 4€ Unterschied macht das 60*4€/2 = 120€ Plus bei Zahlung am Monatsanfang oder 120€ Minus bei Zahlung am Monatsende. (Deshalb bei Kreditverträgen und Zinsverträgen immer aufpassen!!) Wir sind hier in der tabellarischen Rechnung von Zahlung am Monatsanfang (im ersten Monat gabs tatsächlich schon 4€ und nicht 0€ – oder richtigerweise 2€! – von der Oma) ausgegangen. (Wer selber verstehen und also üben will, kann das Ganze ja einmal taggenau rechnen – die Konstanten a, b und c entsprechend auf den Tag beziehen oder die sonst unterschiedlichen Zeiteinheiten beachten – und den neuen Fehler bestimmen!)
Beispiel 2:
Kennt man zu jedem Zeitpunkt die Komponenten der Kraft, die auf eine frei bewegliche Masse wirkt, so kann man deren Komponenten der Beschleunigung bestimmen. Diese verändert in einem Zeitabschnitt die Komponenten der Geschwindigkeit um einen bestimmten Betrag. Man erhält also durch Summation sukzessive alle Werte der Geschwindigkeit. Wiederholt man das Ganze dann noch einmal für den Zusammenhang zwischen Geschwindigkeit und Ort, bekommt man die zeitgetaktete Bahnkurve des Objekts.
Das ist eine riesige Fleißarbeit (man füllt nämlich eine gewaltige Tabelle mit vielen Zeilen (Takte) und Spalten (Werte der Wirkungskette) sukzessive aus), die man allerdings dem PC überlassen kann, entweder programmiert in einem Tabellen-Kalkulations-Programm (z.B. MS-EXCEL) oder in einer „echten“ Programmiersprache. In beiden Fällen muss man die dazugehörigen Formeln nur einmal eingeben und kann dann über Kopieren (EXCEL) oder entsprechende Schleifen (Programm) den interessanten Bereich überstreichen.
Schönes Beispiel aus dem Jahr 2016: Mit den drei „großen“ Enkeln wollte ich im Urlaub voraussehen, wie weit unsere Wasser-Raketen denn fliegen könnten: Wir ermittelten theoretisch etwa 75 m und maßen anschließend auf dem Feld 74 m (Video-Stills anbei)!

Oberfläche für die Flugbahnberechnung in den Phasen „Brennen“ und „Weiterfliegen“ mit Luftwiderstand (Stützstellenabstand hier knapp 2 Tausendstelsekunden)
Die numerische Integration hat natürlich den geschwindigkeitsabhängigen Luftwiderstand berücksichtigt. Die Abweichung von der idealen Parabel ist zu sehen und bei entsprechender Parameter-Änderung noch viel deutlicher möglich. (Die Beiwerte hätte man natürlich durch die Messung einer Fall-Endgeschwindigkeit der leeren Rakete von einem hohen Turm ermitteln können…, so wie ich es mit Studenten für den Beiwert für Autos gemacht habe, die eine Autobahn bekannter Neigung in Dresden West ohne Antrieb herabrollten.)
Beispiel 3:
Es ist für viele Menschen faszinierend, die hell angestrahlte ISS im Sommer am dunklen Abendhimmel lautlos vorbeigleiten zu sehen. Für mich ist es das auch. Man bemerkt, dass sie jeden Abend zu anderer Zeit vorbeikommt, dass auch ihre Zugrichtung ertwas anders ist, dass aber die Zeiten im Abstand von 2 Tagen sehr ähnlich sind und einem Rhythmus folgen. (So etwa haben sich unsere Vorfahren in den Lauf der Gestirne hineingedacht…)
Bald ergibt sich die Frage, ob man das auch allein berechnen kann (wer sich für die möglichen Zeiten der Sichtbarkeit interessiert, hat eine entsprechende App zur Hand…)?
Und kann man sich überhaupt ganz allein überlegen, was man für die Berechnung alles braucht? Welche Zusammenhänge („Gesetze“) und welche Daten?
1. Ein eigenantriebsloser Gegenstand bewegt sich im luftleeren Raum (also ohne Reibungsverluste seiner Energie) entsprechend den auf ihn wirkenden Kräften und entsprechend seiner Masse mehr oder weniger beschleunigt. Das klingt nach dem Newtonschen Gesetz der Proportionalität von Kraft und Beschleunigung. Richtig! Welche Kräfte wirken? Nur die gravitativen wollen wir berücksichtigen, und die sind den beiden Massen proportional und auch dem reziproken Quadrat ihrer Entfernung (ihre rechnerische Gleichheit wird vermittelt durch die Gravitationskonstante).
2. Nach den Gesetzen von der Erhaltung des Drehimpulses und der Energie stehen Abstand und Geschwindigkeit in Beziehung, wobei auch eine potentielle Energie neben der kinetischen bettrachtet werden muss, und außerdem liegt die Bahn in einer Ebene (die Richtung des Drehimpuls-Vektors ist ebenfalls konstant, nicht nur sein Betrag). Im allgemeinen Fall ergibt sich eine Ellipse (also eigentlich eine stabile Schwingung um einen Mittelwert des Abstands, um je einen Mittelwert der kinetischen und der potentiellen Energie (deren Summe natürlich immer konstant ist), deren Sonderfall ein Kreis wäre, bei dem alle Werte konstant sind (außer dem der Flugrichtung…).
3. Wendet man das auf die ISS an, die um die Erde kreist, so scheint das trivial, wenn man eine Kreisbahn annimmt. Setzt man Radialkraft (Anziehungskraft der schweren Massen) und Zentrifugalkraft (Trägheitskraft auf gekrümmter Bahn) gleich, kann man dann die Gleichung nach der Geschwindigkeit umstellen:
| F=m*v²/r=m*M*G/r² |
| v=Wurzel(M*G/r) |
Man sieht, die Eigenmasse des kreisenden Körpers kürzt sich weg.
Setzt man für r den Erdradius, erhält man die erste kosmische Geschwindigkeit.
Wenn man 42.500 km (in etwa 400 km Höhe über der Erdoberfläche) mit knapp 8 km/s (z. B. 7.659 m/s oder 27.572 km/h) fliegt, so braucht man reichlich anderthalb Stunden, schafft also knapp 15 Umdrehungen am Tag.
4. Dabei dreht sich unter einem aber die Erde weg, und zwar genau einmal am Sternentag. ABER: Da es uns um die Sichtbarkeit geht, brauchen wir Dämmerung, damit das beleuchtete Ding vor dunklerem Himmel zu sehen ist, und damit auch die ISS nicht im Erdschatten ist. Also brauchen wir am besten die Tageszeit nach dem Sonnentag, nach dem wir auch unsere Uhrzeit eingerichtet haben. Das bedeutet, dass die Sonne täglich etwa 1° (360°/365d) neben der Position des Vortags steht oder – im Umkehrschluss! – die Ebene der ISS sich gegenüber der Schattenlinie durch die Sonnenbestrahlung um 1° dreht.
Wer ein gutes Vorstellungsvermögen hat, sieht jetzt vor seinem geistigen Auge eine Erdkugel, die zum Beispiel von rechts Sonnenstrahlen empfängt (rechts ist es also hell und links dunkel), die sich auf der uns zugewandten Seite von links nach rechts dreht (dann ist Norden oben), und die von einer schrägen (51,6° zum Äquator) ISS-Bahn eingefasst ist (400 km Flughöhe sind etwa 6% des Radius). Behalten wir in Gedanken eine Position bei, die die Sonne immer von genau rechts auf die Erde scheinen lässt, so schneidet die Schattenlinie den Äquator immer genau in der Mitte unseres Gesichtsfeldes. Zum Frühlings- und zum Herbstanfang ist die Sonne in der Äquatorebene, im Sommer darüber, im Winter darunter.
Die ISS-Bahn schneidet den Äquator aber täglich anders (wenn wir den Ort der Sonne wegen der konstantvgeünschten Schattenlinie auch konstant lassen, obwohl sich die Erde um die Sonne dreht, so müssen wir nun die Ebene der ISS-Bahn im Gegenzug sich drehen lassen taumeln lassen, nämlich um die o.a. 1°/d etwa), so dass es einmal im Jahr eine günstige Konstellation zur Morgendämmerung und einmal im Jahr eine solche zur Abenddämmerung gibt.
Genaueres erhält man, wenn man überlegt, wei weit entfernt vom Beobachtungspunkt auf der Erde die ISS noch über dem Horizont erscheint, wie weit die Dämmerung geht, wo die ISS in den Erdschatten tritt, so kommt man auf konkrete Zahlen zum Rechnen. Dazu braucht man Kenntnisse über Kreise und Kugeln und also etwas sphärische Geometrie sowie den Pythagoras bzw. Winkelfunktionen.

Dann rechnet man alles ganz genau und vergleicht es mit der Wirklichkeit und ist völlig geplättet, dass die ganz anders aussieht: Statt einmal im Jahr morgens und abends die ISS sehn zu können, passiert das alle 2 Monate etwa. Was ist an unseren Überlegungen (meinen!) falsch?
Die 6% Abstand, die die ISS vom Erdball hat, sind zu wenig, um die Abplattung der Erde vernachlässigen zu können. Der „dicke Äquator“ zieht die ISS schneller zu sich zurück, als es bei einem Flug um ein schwarzes Loch im Erdmittelpunkt geschehen würde. Folge: Die ISS-Bahn „taumelt“ zusätzlich zu dem kleinen Betrag durch die Rotation unseres Bezugssystems um einen größeren mehr, als wir angenommen hatten: Über 5°/d, also etwa 1/3 ° pro Erdumrundung. Das ist nicht viel, „läppert“ sich aber schnell zusammen, in reichlich zwei Monaten einmal komplett rum! (Auch der Drehimpuls der ISS-Bahn macht also eine rotierende Richtungs-Schwingung – und das sogar im Sternen-Bezugssystem – , ohne seinen Betrag zu ändern.)
Modelliert man das (EXCEL mit VBA), kommt man daruf, dass man den Äquator mit einem Ring von etwa einem halben Prozent der Erdmasse verstärken muss, um aus der Überlagerung der Kräfte der im Erdmttelpunkt liegenden 99,5% der Masse (in ihrer Wirkung äquivalent einer homogenen Kugel gleicher Masse) und der Ringmasse genau jene Bahn zu erhalten, die die ISS tatsächlich nimmt.
Hier der Basic-Programm-Ausschnitt zur Bestimmung der Knotenwanderung:
‚Berechnung der Bahn
‚1. Startposition und Startgeschwindigkeit
xiss = riss: yiss = 0: ziss = 0
vxiss = 0: vyiss = voiss * Cos(aiss): vziss = voiss * Sin(aiss)
‚2. numerische Integration von Geschwindigkeit und Ort aus den Kräften
t = 0: zissalt = 0
j = 0
Do While Not (((zissalt < 0) And (ziss > 0)) Or t > 10000)
j = j + 1
t = t + dt
‚Kraftberechnung
‚Kraft der Kugel
fxiss = -mer * xiss / (xiss ^ 2 + yiss ^ 2 + ziss ^ 2) ^ (3 / 2)
fyiss = -mer * yiss / (xiss ^ 2 + yiss ^ 2 + ziss ^ 2) ^ (3 / 2)
fziss = -mer * ziss / (xiss ^ 2 + yiss ^ 2 + ziss ^ 2) ^ (3 / 2)
zissalt = ziss
‚Kraft des Ringes
For i = 1 To ns
fxiss = fxiss + ms / ns * (xs(i) – xiss) / ((xs(i) – xiss) ^ 2 + (ys(i) – yiss) ^ 2 + (ziss) ^ 2) ^ (3 / 2)
fyiss = fyiss + ms / ns * (ys(i) – yiss) / ((xs(i) – xiss) ^ 2 + (ys(i) – yiss) ^ 2 + (ziss) ^ 2) ^ (3 / 2)
fziss = fziss + ms / nziss) / ((xs(i) – xiss) ^ 2 + (ys(i) – yiss) ^ 2 + (ziss) ^ 2) ^ (3 / 2)
Next
‚Integration der Beschleunigung zur Geschwindigkeit
vxiss = vxiss + dt * fxiss
vyiss = vyiss + dt * fyiss
vziss = vziss + dt * fziss
‚integration der Geschwindigkeit zum Ort
xiss = xiss + dt * vxiss
yiss = yiss + dt * vyiss
ziss = ziss + dt * vziss
Cells(18 + j, 4) = t: Cells(18 + j, 5) = xiss: Cells(18 + j, 6) = yiss: Cells(18 + j, 7) = ziss
Loop
‚Knotenverlagerung pro Umlauf
dkniss = -Atn(-yiss / riss)
Der Index i bei den Koordinaten xs(i) meint die Nummer der den Ring darstellenden Einzelmassenpunkte, über die die Gesamtkraft aufsummiert wird.
So haben wir jetzt also – ohne Verwendung der Kreiselgesetze! – die Präzession des ISS-Bahn-Kreisels durch das Kippmoment der geplätteten Erde berechnet!
(Diese Behauptung ist natürlich selbst wieder ungenau, denn die Achse der Bahn präzidiert nicht gleichmäßig, sondern ergibt sich aus der Zusammensetzung eines Großkreisbahn-Anteils und einer S-Kurve bei jeder Äquator-Kreuzung: Der Zusatz-Ring um den Äquator beschleunigt bei Annäherung zum Äquator hin und bremst bei Entfernung wieder ab, so dass wieder ein Großkreisbogen, aber eben etwas verdreht, beflogen wird, usw. usf.)
Der Spaß am Spielen mit allen freien Parametern des Programms entschädigt für den Aufwand seiner Erstellung.
Natürlich gibt es bei Wikipedia fertige Formeln zur Berechnung, aber selber essen macht fett…
(Durch häufige Bahn-Anhebungen der ISS, die täglich etwa 50 m sinkt, sind auf die Sekunde genaue Vorhersagen nur für einige Tage möglich, aber so ungefähr bekommt man es wirklich hin!)
Beispiel 4:
Nachprüfung, ob eine kugelsymmetrische Massenverteilung in ihrer Gravitationswirkung auf außerhalb befindliche Massen durch ihre Gesamtmasse im Schwerpunkt ersetzbar ist (nicht-relativistisch), wie wir das in der Schule (ohne Beweis!) gelernt haben.
Hier nutzen wir die große Freiheit der numerischen Integration, die darin besteht, dass die Art der Zerlegung des gesamten Objektes in einzelne Teile völlig unserem Gespür für mathematisch-physikalische Zweckmäßigkeit unterliegt. Der Pfiffigste von uns findet also die eleganteste Lösung. Wir wissen schon: Symmetrie-Überlegungen erleichtern die Arbeit u.U. gewaltig.
Also: Einfach anfange. Eine Kugel sei mit Masse konstanter Dichte gefüllt („homogen“). Falls für jede Kugelschicht gelten sollte, dass ihre Wirkung durch ihren Schwerpunkt ersetzt werden kann, so gilt das superpositionell auch für die ganze Kugel.
Die Kugelschicht mit der Masse m1 mit dem Radius r und der Dicke d zerlegen wir nun in Ringe um eine Achse, die von der außerhalb befindlichen Probemasse m2 (imAbstand s > r zum Mittelpunkt MP der Kugelschicht) zum MP der Kugelschicht verläuft und in der x-Achse liegen soll. Die Ringe sollen sich durch ihren Winkel α unterscheiden, der vom MP aus zwischen x-Achse und Ring (also zum Beispiel seinem Schnitt mit der x-y-Ebene) gebildet wird. Die Ringbreite ist am besten konstant und über einen Winkel dα festzulegen.
Jeder Punkt eines bestimmten Ringes hat dann denselben Abstand zur Probemasse m2 und also dieselbe Kraftwirkung. Die Kraftwirkungen der Ringpunkte in y- und z-Richtung heben sich „aus Symmetriegründen“ paarweise auf, so dass wir nur die x-Komponenten zu berücksichtigen haben.
Addieren wir die Kraftwirkungen aller Ringe (die unterschiedlichen Abstand zu m2 und unterschiedliche Massen wegen ihrer unterschiedlichen Radien bei gleicher Dicke haben), so erhalten wir die Gesamtkraft und vergleichen mit der Gesamtkraft zwischen zwei Punktmassen.
Ergebnis:
Im Dreidimensionalen geht diese Rechnung tatsächlich auf!
Die Probe für die Richtigkeit der Rechnung besteht im Variieren des Abstands von m2, denn für große Abstände muss sich das Problem dem der Punktmasse sowieso sehr schnell nähern und für ganz kleine Abstände müssten nur kleine Fehler der endlichen Anzahl von Integrationsschritten sichtbar werden.
(Man kann die Kugel auch komplizierter aufteilen, auch dann geht das selbstverständlich auf, auch wennd er Aufwand enorm wächst!)
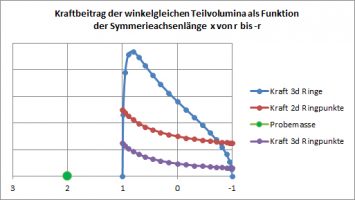
Forscht man weiter und versucht das Ganze mit 2 Dimensionen, so stellt man fest, dass das dort nicht geht: Die näher gelegenen Anteile (hier sind es Bögen von Kreisringen) überwiegen sowohl im zylindersymmetrischen („echt zweidimensionelen“) Modell (selbst bei 10-fachem Radius als Abstand der Probleadung noch um 4%) als auch im kugelsymmetrischen Ansatz (sogar um 10%!) des Gravitationsgesetzes und führen zu einer höheren Anziehungskraft als der einer Masse allein im Schwerpunkt.
Es ist aber nur halb so schlimm: Im Dreidimensionalen sind die „hinteren Ränge“ dichter besetzt, weil der Ring der Kugelschicht erst in einem Abstand, der größer als der zum Mittelpunkt ist, seinen maximalen Umfang hat und somit einen massemäßig großen Beitrag zur Kraft-Summe liefert, während im Zweidimensionalen alle winkelgleichen Masse-Anteile auch gleich groß sind. Um die Scheibe in ihrer Wirkung der Kugel anpassen zu können, müsste man für die Schwerpunkt-Rechnung diesen im obigen Beispiel des Abstands 2 der Probemasse vom Ursprung für die 3d-Rechnung um etwa 75% des Radius der Probemasse entgegenschieben, bei einem Abstand 3 noch um etwa 65%!
HOPPLA! STOPP! Beim Abendbrot habe ich meiner Frau erzählt, was ich heute (Sonntag!) gerechnet habe. Und da habe ich bemerkt, was das für ein Stuss ist! Wenn ein Kreisring als Teil eines Kreises (einer Scheibe) gravitativ NICHT durch seinen Schwerpunkt ersetzt werden kann, so darf er auch nicht mehr repräsentativ für die gesamte Scheibe stehen, wie das bei der Kugelschale für die gesamte Kugel erlaubt war! Dann muss man eben die übrigen Ringe ebenfalls noch berechnen, um den gravitativen „Schwerpunkt“ in Relation zum Mittelpunkt oder herkömmlichen Schwerpunkt im homogenen eindimensionalen Feld setzen zu können. Es ist zu erwarten, dass dadurch die Abweichung von der Schwerpunktsrechnung geringer wird, weil der relative Abstand der Probemasse zum Ringradius wächst und der gravitative Schwerpunkt bei der Addition der Wirkung der einzelnen Ringe dadurch schrittweise Richtung Mittelpunkt wandert, ohne ihn allerdings erreichen zu können.
Also:
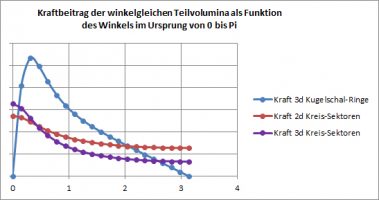
Wenn man die inneren Ringe (hatte nur mit dem äußeren gerechnet, weil der am stärksten abweichen sollte, sofern er pberhaupt abweicht) tatsächlich noch hinzurechnet, dann kann man also die Winkelabhängigkeit als die Summation von Kreissektoren betrachten, während die Längenabhängigkeit sich dann auf die Mittellinie des äußeren Rings bezieht.
Jetzt ist zur Verstärkung des noch verbliebenen Effekts ein geringerer Abstand der Probemasse gewählt worden. Die erforderliche Verschiebung des hypothetischen Gravitations-Schwerpunktes beträgt aber immerhin noch 6% im 2D- und 14% im 3D-Fall. Das ist nicht viel, aber für die Berechnung von Bahnen sehr wesentlich!
Interessant ist dieser Unterschied insbesondere bei der Betrachtung von Bewegungen in flachen Galaxien, weil die Lage des „scheinbaren“ Schwerpunkts abstandsabhängig wird. Genau betrachtet führt es aber zur gleichen Überlagerungs-Anschauung wie bei der Berechnung der ISS-Bahn (oben unter Beispiel 3) unter Beachtung der „echten“ Geoid-Form der Erde als Superposition von Kugel und Ring, nur unter anderem Winkel.
Man sollte also ein Untersuchung einer Satelliten-Bahn um eine Kreisring und um eine Kreisscheibe in deren Ebene anstellen (also ohne Präzession eines geneigten Drehimpulses) und die zu erwartende Abweichung von der stationären Ellipse (auch ohne Berücksichtigung der endlichen Lichtgeschwindigkeit!) dokumentieren. (Kommt bald!)
Im Eindimensionalen (Stab wird quer in gleich große Längs-Stücke geteilt) hingegen herrscht übrigens wieder scheinbar Identität mit der Schwerpunkt-Rechnung wie im Dreidimensionalen, da alle Beiträge zur Summe im Feld konstanter Stärke sowieso lageunabhängig gleich groß sind. (Dieses Ergebnis könnte Ausgangspunkt wüster philosophischer Debatten sein!)
Beispiel 5:
Überlegungen zur Wahl der schnellsten Ski-Abfahrts-Linie auf einer gegebenen (nicht zu schmalen) Strecke.
Wir können das Problem hier nicht komplett lösen, aber wir können es in Teile zerlegen und zusammensetzen und uns erst einmal Gedanken zum Problem selbst machen: Es ist eine Fragestellung aus der Klasse der „Variationsaufgaben„, nämlich jene Parameter durch Variation zu finden, die in einer bestimmten Hinsicht ein Optimum ergeben. (Die Methode heißt dann „Variationsrechnung“ und hat mit komplizierten Integralen zu tun. Diese wollen wir hier in diesem Abschnitt nicht lösen, sondern nur Beispiele numerisch integrieren. Im Zweidimensionalen der x-z-Ebene wäre eine Zykloiden-Bahn die Lösung.)




Kommentar abgeben