2.8.4 Trajektorien um nicht rotationssymmetrische Konstellationen
Auch in diesem Abschnitt soll Wert auf heuristisch/didaktische Steigerung der Schwierigkeit gelegt werden. Die Ermittlung der Ergebnisse erfolgt stets durch numerische Integration, welche hier nicht im einzelnen erläutert wird.
Beginnen wir also:
Fall 1: Schwerkraft-Trajektorien um 2 feste Punkte (kommt in der Schwerkraft-Natur nicht vor, wäre aber elektrisch zu konstruieren)
Es lässt sich natürlich eine Startgeschwindigkeit einstellen, die ortsabhängig so zum Feld passt, dass eine stationäre Bahn entsteht, die an die symmetrische Schwingungs-Ellipse erinnert:
Links der existierende, aber schwer zu findende Idealfall mit stationärer Ellipse, rechts der allgemeine Fall mit Apsiden-Drehung. Der ensteht auch durch alleinige Veränderung des Zentralmassen-Abstandes. (Schwarz ist die Vergleichsellipse bei gleichen Startwerten um eine einzige Punktmasse gleichen Gesamtbetrages.) Verringert man den Zentralmassen-Abstand weiter, geht die Bahn in die Kepler-Ellipse über (wie schon im Abschnitt 2.8.1 ausführlich behandelt):
Vergrößert man den Abstand der Zentralmasse weiter, so kommt es irgendwann zur Kollisions-Katastrophe, vorher aber zu tollen Rosetten:
Fall 2: Schwerkraft-Trajektorien um 2 rotierende Punkte (in der Natur als Doppelstern bekannt)
Hier erwartete man grundsätzlich keine stationäre Bahnen, sondern eventuell eine zufällige Schwebung der Rosette, besonders, wenn beide Zentralmassen ähnlich groß sind. Aber: Bei Gleichheit der Zentralmassen und Kreisförmigkeit ihrer (dann identischen!) Bahn kann die Probemasse-Bahn auch kreisförmig sein (siehe weiter unten als Spazialfall im Fall 2).
Dargestellt werden immer alle drei Bahnen (zwei Zentralmassen und ein Planet) samt Verbindungs-Strahlen zu fünf ausgewählten (und stets gleichen) Zeitpunkten im linken Diagramm, dann der Zeitverlauf von Abstand und Winkelgeschwindigkeit der Verbindungslinie beider Zentralmassen (sowie rechts die Probe über die Konstanz Drehimpulse der Zentralmassen und ihrer Summe).
Zuerst eine Bahn im Idealzustand zweier gleicher Zentralmassen auf identischer Kreisbahn:
(Die leichte Drift ist ein Numerik-Artefakt.)
Hier eine Bahn mit Zentralmassen gleicher Größe und elliptischer Bahn:
Man kann mit den Parametern spielen (u.a. wachsende Irritation der grünen Planeten-Bahn durch zu große Nähe):
Zum Schluss noch eine nahe Bahn um schwach ungleiche und stark elliptische Zentralmasse-Bahnen:
Nachbemerkung: Mit meinem handelsüblichen PC will ich nicht größere Systeme bearbeiten, weil dabei die Stabilität der Numerik unklar wird. Man kann dann nicht mehr unterscheiden, ob Rosetten „echt“ oder numerische Artefakte sind. Mit Großrechnern ist man heute in der Lage, das Abkippen eines Sandhaufens diskretisiert zu behandeln – also jedes Sandkorn für sich – oder das globale Wetter zu modellieren. Ich bin also bescheiden und begnüge mich hiermit, denn der Zweck ist erfüllt: Das Wundern über das Wandern des ISS-Knotens ist dem Verständnis für die Zusammenhänge gewichen.
Übrigens: Das gemessene Achsverhältnis der beiden folgenden Ellipsen ist auf 8 Stellen identisch, was bei reichlich 60.000 Zeilen EXCEL-Integration ( hier 6,5 Umdrehungen der Zentralmassen – links herum – und über 3 Umdrehungen des Planeten – rechts herum – : Drehrichtungen also ungleichsinnig) erstaunlich ist.
Die mittlere Apsidendrehung der Umlauf-Ellipse entspricht voll der im vergangenen Abschnitt erarbeiteten Theorie.
Zwei weitere Einstellungen (Drehrichtungen gleichsinnig!) sollen den Übergang zum nächsten Abschnitt einleiten: „Schwungholen“ gezielt oder chaotisch.
Im linken Bild ist der Planet am Ende der Integrationszeit etwa 300 Längeneinheiten vom Zentrum entfernt und entfernt sich immer noch langsam.
Trotzdem bleibt eine heuristische Frage offen:
Kann es einen Spezialfall geben, bei dem sich eine Dreier-Konstellation von zwei Zentralmassen (Doppelstern) und einem Planeten mit gemeinsamer Winkelgeschwindigkeit (also konstanten Abständen) um sich selbst dreht?
Nach der „Überlegung 2“ im Punkt 2.8.3 ist klar, dass das VSZ („virtuelles Schwerkraftzentrum“) zweier Zentralmassen bezüglich einer auf der gleichen Geraden liegenden Probemasse vom Schwerpunkt weg zu dieser hin verlagert ist. Daraus erwächst die Möglichkeit, dass es einen Abstand gibt, für den das Gleichgewicht von Schwerkraft und Zentrifugalkraft hergestellt ist und eine mit den Zentralmassen synchrone Kreisbahn entsteht.
Das wollen wir hier untersuchen.
Fall 2a: Planet auf der Verbindungsgeraden des Doppelsterns im Abstand r vom SP (symmetrischer Doppelstern auf identischer Kreisbahn):
Normiertes Schwerkraftgesetz (Doppelsternbahnradius = 1, G*M*m=1):
Fs = 1/(r+1)² + 1/(r-1)²
Zentrifugalkraft (w: Winkelgeschwindigkeit):
Fz = w² * r
Die Zusatzforderung der Gleichheit der Winkelgeschwindigkeiten von Doppelstern und Planet eröffnet die Möglichkeit für eine Bestimmungsgleichung, denn die Winkelgeschwindigkeit des Doppelsterns ergibt sich ebenfalls aus den zwei Gleichungen für Schwerkraft Fsd und Zentrifugalkraft Fzd:
Fsd = 1/(2R)²
Fzd = w²*R
w² = 1/4R³
Oben eingesetzt (gleiches w gefordert und r/R=r gesetzt) ergibt
r/4 = 1/(r-1)²+1/(r+1)²
r5 – 2r3 – 8r2 + r – 8 = 0
Ergebnis: Es gibt tatsächlich einen solchen Planetenbahnradius für eine stationäre Bahn mit
r = 2,397 R
Fall 2b: Planet auf der Mittelsenkrechten des Doppelsterns im Abstand r vom SP (symmetrischer Doppelstern auf identischer Kreisbahn):
Die gleichen Überlegungen wie oben führen mit Hilfe der Berechnungen im Punkt 2.8.3 zu
r/4 = 2/(r²+1)3/2
r = √3 R = 1,732 R
Auch hier gibt es tatsächlich einen solchen „stationären“ Ort für einen Planeten.
Aus Symmetriegründen gibt es somit also vier Positionen für stationäre Planeten.
Gemetrisch sieht das so aus:
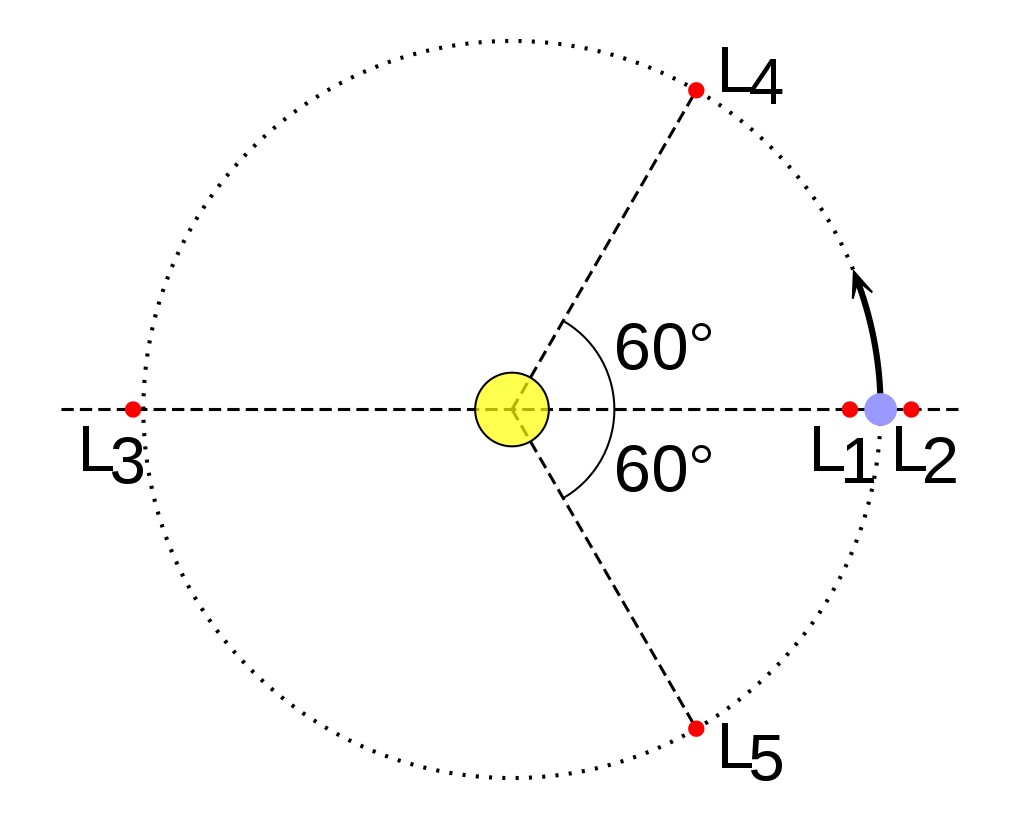
Die hier ermittelten Punkte sind Spezialfälle (siehe 2.8.4.1!) der allgemeineren Lagrange-Punkte L2 bis L5 eines einfachen Sonne-Planeten-Systems: L2 und L3 sind längs, L4 und L5 quer; L1 läge bei uns oben im Zentrum des symmetrischen Doppelstern-Systems.
(Das oben dynamisch errechnete Ergebnis r = √3 R spiegelt sich in dieser Skizze im gleichseitigen Dreieck wider!)
Die Plots der Kraftfunktionen für Schwerkraft und Zentrifugalkraft in beiden Fällen sehen so aus:
Modelliert man das durch numerische Integration, kommt man auf gute Plots der Bahnsysteme (Verbindungslinien veranschaulichen wieder die Positionen zu ausgewählten Zeitpunkten), die die analytischen Berechnungen exakt bestätigen:
Verfeinert man das numerische Modell und lässt auch unsymmetrische Doppelsterne der Masseverhältnisse 2:1 bis 10:1 (fast schon Planetensystem) zu, so sind die Langrange-Punkt-Bahnen immer dichter an der Planetenbahn dran, ohne sie aber exakt erreichen zu können (insofern ist das Wiki-Bild ungenau beschrieben, denn alle Bahnen – die Planeten-Bahn wie die Dreieck-Bahn inclusive Zentralgestrin – rotieren nicht um den Mittelpunkt des letzteren, sondern um den gemeinsamen Schwerpunkt!):
Übrigens: Die hier angestellten Überlegungen sind nicht nur von heuristischem Wert, sondern sind auch Start-Gedanken zum Verständnis von galaktischen Strukturen („Balken-Galaxis“!), bei denen die Keplerschen Gesetze außer Kraft gesetzt zu sein scheinen.
(Wer das geneuer beweisen möchte, dass ein gleichseitiges Dreieck eine mögliche Konstellation für synchrone Orbitale ist, der muss so vorgehen:
a) Suche des Bahnradius für m3 (m3<<m2<<m1) aus den physikalischen Bedingungen gleicher Winkelgeschwindigkeit wie Doppelstern und dreimal Fzi=Fsi
b) Suche des Abstandes der Dreieckspitze vom Schwerpunkt des Paares m1-m2 als rein geometrische Aufgabe über den Cosinussatz
In beiden Fällen erhält man exakt die gleiche Beziehung, weil im Cosinussatz Abstands-Quadrate vorkommen und in der Schwerkraft auch.
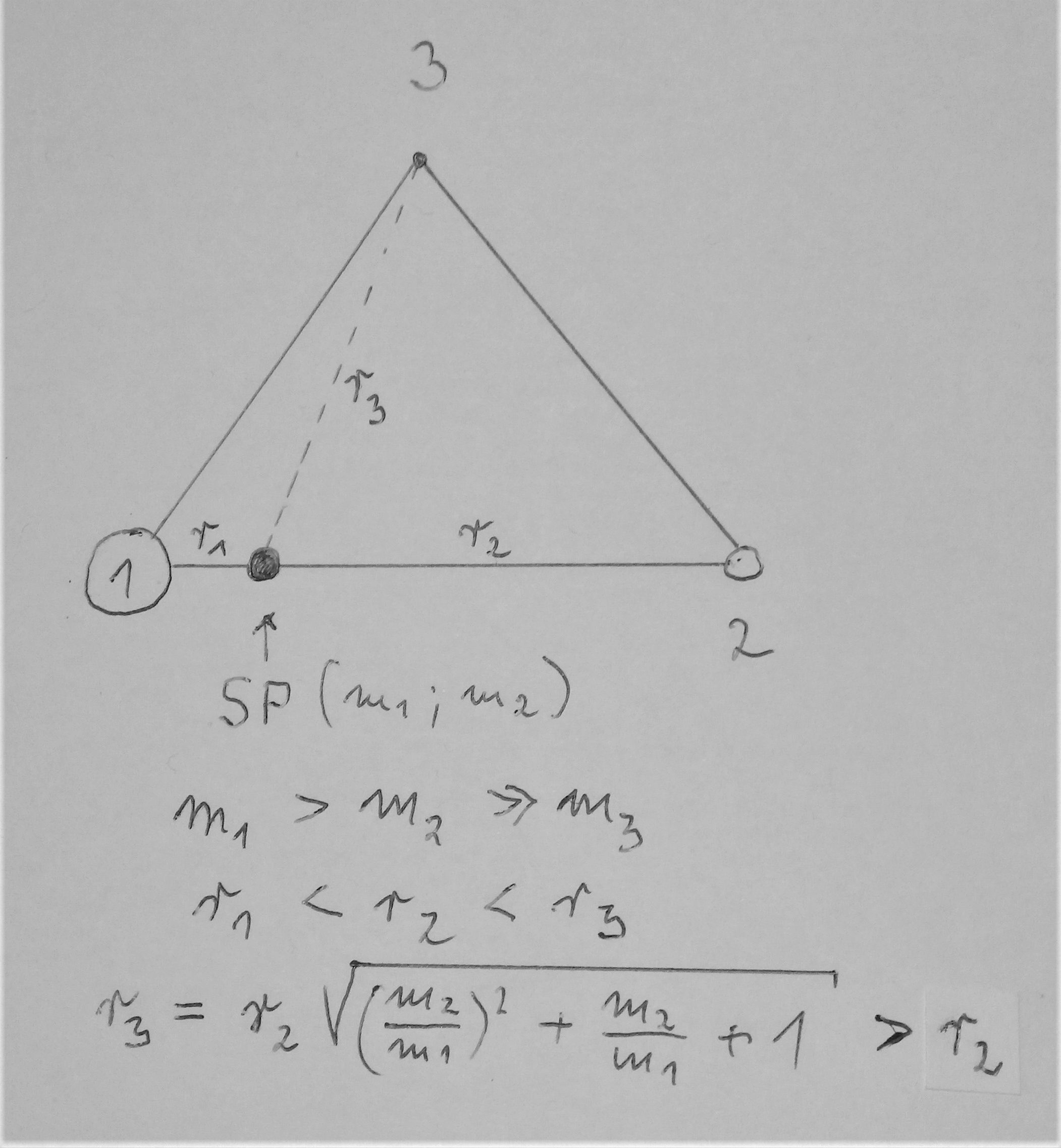
Skizze zur Lage der drei Massen und zu den Radien ihrer synchronen Kreisbahnen um den Schwerpunkt. (Die Indizes 1 und 2 können getauscht werden. Im Grenzfall m1=m2 ergibt sich Wurzel aus 3 als Radienverhältnis, wie oben schon beschrieben.)
Allerdings folgt daraus auch, dass die Wikipedia-Zeichnung ungenau ist, weil der Bahnradius von m3 immer größer als der von m2 ist, solange man nicht m1 anstelle des Schwerpunktes als Ursprung des rotierenden Bezugssystems wählt!
Hier die numerisch modellierten Bahnen für ein Masse-Verhältnis von 40:1 für die beiden „Doppelstern-Zentralmassen“, die nun schon einem echten Planetensystem sehr nahe kommen:

Blau ist die schwere Zentralmasse (m=40), die nur leicht taumelt, rot der Planet (m=1) und grün die sehr leichte Probemasse (m<<1) knapp außerhalb der Planetenbahn und synchron.
Bildet man ein „Potential“ aus Schwerkraft und Zentrifugalkraft im rotierenden System (siehe 2.8.4.1), kann man bei einer 3D-Abbildung in EXCEL die Lagrangepunkte L1 bis L3 wenigstens als Sattelpunkte erkennen, wohingegen die „dynamisch stabilen“ (Probemasse durch die Coriolis-Kraft im azimutal sehr flachen lokalen Potentialmaximum bei kleinen Relativgeschwindigkeiten zu kreisähnlichen Bahnen stabilisiert) Gebiete um L4 und L5 gerade gut genug aufgelöst sind, um ahnen zu können, dass es dort tatsächlich Stabilitätsbereiche geben könnte. Ein Vergleich meines modellierten Potential-Doppel-Kraters (Links: Nur Zentralmasse; Mitte: Masseverhältnis 20:1) mit der Wikipedia-Skizze (rechts):
(Auf diesem Wiki-Bild sind nun L3, L4 und L5 auch ganz leicht außerhalb der Planetenbahn – „geht doch“!)
FAZIT:
Es ist für das Verständnis der Natur der Lagrange-Punkte wichtig, dass man begreift, dass diese NICHT durch den Planeten „erzeugt“ werden, sondern dass der Planet den „Lagrange-Ring“ (der Zentralmasse mit einer dazugehörigen Winkelgeschwindigkeit) so zerstört, dass nur zwei Punkte (L4 und L5) dicht neben der ursprünglichen Lage der Ringkrone (Abstand abhängig vom Masseverhältnis Zentralmasse – Planet) als lokale Maxima „übrig bleiben“ und L3 sowie L1 dazwischen als Sattelpunkte hinzukommen. Nur L2 ergibt sich „zusätzlich“ (also erst durch den Planeten „erzeugt“) als Sattelpunkt auf dessen verlängerter Verbindungslinie mit der Zentralmasse.
Die anfangs sehr verwunderlich erscheinende (und durch die Praxis mit etlichen Satelliten schon längst bestätigte und genutzte) Tatsache von geschlossenen Bahnen um die Lagrangepunkte wird zur trivialen Aussage, wenn man bedenkt, dass eine schwach elliptische Kepler-Bahn im konstant mit der mittleren Winkelgeschwindigkeit rotierenden Bezugssystem zum kleinen Kreis um den mittleren Zentralabstand wird: Innen wird der hier feststehende mittlere „Fahrstrahl“ überholt und außen wieder vorbeigelassen. Wer denkt jetzt hier an jahrhundertealte astronomische Uhren mit ihren planetengetriebeähnlichen Konstruktionen? (Bei stärker exzentrischen Ellipsen wird das etwa anders, wie es dort in 2.8.4.1 gezeigt wird.)
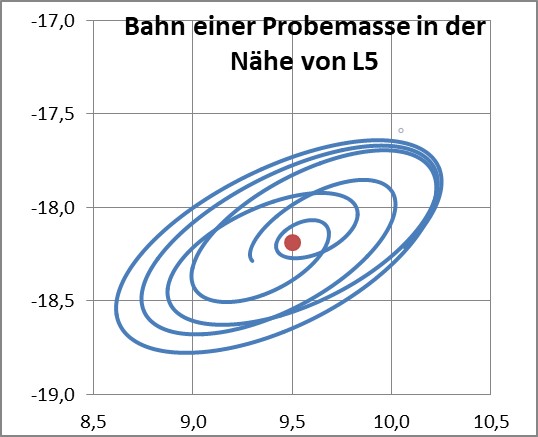
Eine numerische Integration mit nicht-idealen Anfangsbedingungen kann dann Übergangslösungen zwischen enger Fast-Kreis-Bahn und „Hufeisenbahn“ zwischen L4 und L5 erbringen:
Die Richtung des Potentialrückens lässt sich gut an der langgezogenen Bahn erkennen, deren Krümmung dort, wo die Corioliskraft sozusagen eine Gegenkraft hat, geringer ist und deshalb eine ellipsenähnliche Bahn erwirkt. (Es wurde ein kleiner Korrekturfaktor in die Corioliskraft – etwa 1 bis 2% zusätzlich – eingerechnet, um die Artefakte der Numerik auszugleichen.)
(Übrigens: Aus philosophischer Sicht ist das ein interessanter Aspekt der Frage nach der Realität des dreidimensionalen Raumes um nichtrelativistische Phänomene, denn ohne den aus der Dreidimensionalität folgenden Exponenten -2 im Kraftgesetz sähe alles ganz anders aus!)
Fall 3: Schwerkraft-Trajektorien um Ellipsoide
Diese Fälle sind weiter oben schon behandelt worden und sind heuristisch auf die Unterscheidung von Schwerpunkt SP und „Virtuellem Schwere-Zentrum“ VSZ reduzierbar: Je nach Lage des mitrotierenden VSZ ergibt sich eine bestimmt gerichtete Apsidendrehung der ursprünglichen Kepler-Ellipse.
(Übrigens: Beschreibt man die Ellipse des Doppelstern-Partners aus der „eigenen“ Sicht des anderen Partners, ergibt sich keine vergleichbare Rosette, da Synchronisation vorherrscht. Es ensteht vielmehr wieder eine Ellipse, die aber mit anderem Achsverhältnis als bei den beiden untereinander ähnlichen Ausgangs-Ellipsen des Doppelsterns: Das Größenverhältnis spielt eine Rolle, wie man leicht einsieht!)
Bei schräg zur Symmetrieebene (oder Symmetrieachse) gestellten Bahnen heißt das, dass eine Knotenwanderung entsteht. Die Bahnachse präzediert dann ähnlich einer Kreiselachse, und das sogar auch dann, wenn der ideale „Kreis-nahe Zustand“ eingestellt worden ist.
Das sind dann Praxis-nahe Fälle, wie sie durch die ISS und die geneigten Planetenbahnen überall in der Welt vorkommen.
Übrigens kommen dreiachsige Ellipsoide im Weltall nur als genäherte Form für kleine Himmelskörper wie Asteroiden vor. Jegliche Rotation führt im Falle nichtstarrer Körper irgendwann zu rotationssymmetrischen (ellipsoidähnlichen) Formen. Die obige Abhandlung hat also mehr einen heuristischen als einen praktischen Hintergrund. Wie aber die letzten Meteoriten-Missionen gezeigt haben, sind sogar die elastischen Effekte bei der Landung auf solch einem Körper (nach mehrfachem Umrunden in kompliziertem Orbit) hochinteressant. (Tschurjumow-Gerassimenko 2016, Ryugu 2019)
Fazit:
Man kann auch im Umkehrschluss aus der Apsidendrehung auf die Nicht-Kugel-Form der Zentralmasse schließen und ein solches Messverfahren entwickeln (wenn keine weiteren Körper im Spiel sind und relativistische Effekte vernachlässigt werden dürfen). Das passiert allerdings heute schon wesentlich präziser mit sehr komplexen „Schwere-Sensoren“ in Satelliten. (Ihre Komplexität ergibt sich aus der Äquivalenz von träger und schwerer Masse, weswegen mit Kompensationsverfahren entsprechend sensibel aufgehängte Masse-Kombinationen „in Position“ gehalten werden müssen.) Die Ergebnisse sind in Schwerfeldkarten der Erdoberfläche zusammengefasst, aus denen neben der geometrischen Form der Erdoberfläche auch die Variation der Dichte des Untergrunds hervorgeht.



































Kommentar abgeben