Joachim Adolphi

2.4.1.1.2.5 Prüfung der kausalen und numerischen Zusammenhänge

• Joachim Adolphi
• Montag, 30. Oktober 2023
• Dienstag, 31. Oktober 2023
• Balken, Balkenbiegung, Biegung, kausal, Schwingung, Stab, Stabschwingung, Zusammenhang

Nachdem wir oben die faktischen Zusammenhänge, nämlich die numerischen Werte der Oberschwingungen im longitudinalen und im Biegefall, im Modell bestätigen konnten, was auch eine Bestätigung des Modells selbst war, wollen wir noch die kausalen Zusammenhänge zwischen den Frequenzen und den physikalischen Parametern des schwingenden Stabes prüfen: Länge, Dichte (also nicht Gesamtmasse!), Elastizität, Querschnitts-Form (für die Biegung wichtig).

Um nicht durch eine willkürliche Anregung eventuell Schwierigkeiten bekommen zu können, wählen wir die „natürliche“ durch die Schwerkraft

– an einer anfangs kraftlos senkrecht hängenden Schrauben-Feder-Kette für die longitudinalen Schwingungen

– an einem anfangs waagerecht eingespannten Spiral-Feder-Stab ohne Belastung für die Biegeschwingungen

wobei die Schwerkraft „plötzlich“ eingeschaltet wird und die Anordnung aus ihrer Ruhelage bringt. Wir untersuchen dann die entstehenden ungedämpften Schwingungen, indem wir die Parameter ändern.

Beginnen wir mit

1. Abhängigkeit von der Länge L (errechnet aus als Anzahl n der Einzelmassen der Größe m multipliziert mit dem Abstand l zwischen den Einzelmassen: L = n*l in [m])

 

Wir lassen also alle anderen Parameter konstant und verändern nur die Länge (und damit wegen konstant gehaltener intensiver Größe Dichte rho = m/l auch die extensive Größe Masse!).

a) Längsschwingung

Wir beschränken uns auf drei Werte und schauen, ob ein eindeutiger Zusammenhang möglich erscheint:

Daraus ergibt sich folgende Tabelle (Schwingzeit ablesen, Frequenz berechnen, vermuteten Zusammenhang testen):

fo = f(L)			Funktion	Prüfung
L	T	fo	1/L	K=fo/(1/L)
20	32,5	0,0308	0,050	1,63
40	63,7	0,0157	0,025	1,59
60	96,7	0,0103	0,017	1,61

In der Konstanten K müssen also alle anderen Einflussgrößen, die wir weiter unten untersuchen wollen,  enthalten sein. Es wurden händisch verschiedene Funktionen getestet, mis ein zufriedenstellendes Ergebnis erzielt worden ist, und das stimmt mit der Theorie für die querschwingende Saite oder längsschwingende Luftsäule überein. (Man kann die Funktion auch mit der EXCEL-Trendlinie als Potenzfunktion suchen lassen, wie unten im Diagramm gezeigt.) Wir dürfen annehmen, dass wir es hier mit dem Schwingungsbild einer „halben Saite“ oder „halben Luftsäule“ zu tun haben, was nichts an dem grundsätzlichen Zusammenhang

(L1)    Proportionalität zur reziproken Länge f_o ~ 1/L

ändert. (Das hängt, wie wir wissen, mit der Laufzeit der sich mit längenunabhängiger Schallgeschwindigkeit bewegenden Welle zusammen.)

fo = f(L)			Funktion	Prüfung
L	T	fo	1/L	K=(1/L)/fo
20	32,5	0,0308	0,050	0,62
40	63,7	0,0157	0,025	0,63
60	96,7	0,0103	0,017	0,62

Die Konstante K ist jetzt reziprok zur obigen angesetzt, um mit dem EXCEL-Wert der Trendlinie besser vergleichen zu können:

b) Biegeschwingung

Wir nehmen die Stablängen von 10, 20 (Standard) und 40 Massen (wir stellen uns diese Massen als massebehaftete ebene spiralige Torsionsfedern vor, etwa wie in einem mechanischen Feder-Uhrwerk, die untereinander in Reihe senkrecht zu ihrer Achse durch masselose Stäbe verbunden sind) im Abstand 50 zum Messen (Beim Biegen spielt der Abstand nun tatsächlich eine Rolle!):

Standardwerte im Modell (nicht alle sind bei jeder Einstelklung wirksam):

Biegeschwingung	Lineare Näherung für kleine Winkel: y=L*sin(beta)=L*beta
Zusatzmasse Ende zm	0	0
Anzahl n	20
Gelenk-Konstante kg	1
Gelenk-Abstand L	50
Anregungsart art	5	1 einm; 2 sin; 3 x²; 4 x²-x/x^4-x^2; 5 Bieg+SK; 6 Keil-Zunge linear
Anregungs-Amplitude ya	0
Anregungs-Masse am	29
Element-Masse em	1
Einspannungs-Art ea	1	2 2 Aufl; 1 eins; 0 nicht
Taktzahl nt	10000	=<40000
Zeittakt dt	2
Dämpfung D	0
Anreg-Per-Zeit tP	0,0000001
Anr-Per-Anzahl tN	2
Erdbeschleunigung G	0,02
Strobo-Blitze ns	40

Hier nun die Ergebnisse:

Man erkennt deutlich eine jeweilige Viertelung der Frequenz, noch deutlicher, wenn man zwei Diagramme überlagert:

 

Daraus ergeben sich wieder folgende Werte:

lo=	50
n	L	fo	K=L²*fo
10	1000	0,0005300	530,0
20	2000	0,0001340	536,0
40	4000	0,0000320	512,0

und daraus folgendes Funktionsbild:

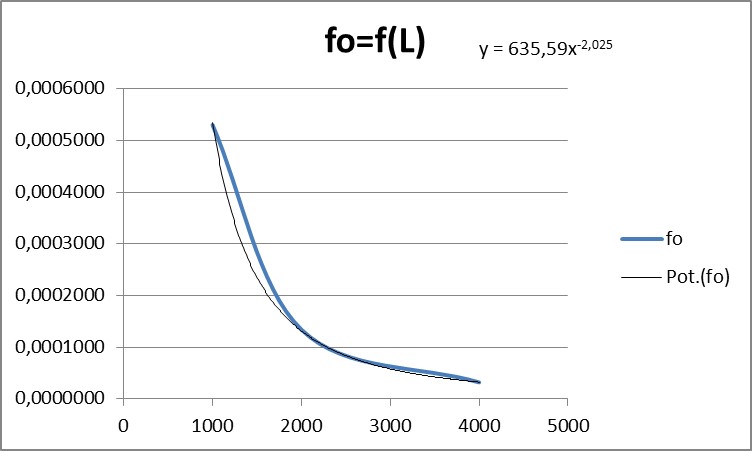
Der erste Zusammenhang ist also

(L2)   Proportional. zum Quadrat der rezipr. Länge:  fo(L) ~ 1/L²

Der Unterschied zur Längsschwingung ist gravierend, aber verständlich: Das lose Ende muss ja hin- und hergeschleudert werden. Wir haben hier das Trägheitsmoment ja nicht explicit eingeführt, es ergibt sich quasi von allein durch die entsprechenden Excelperimente!

 

2. Abhängigkeit von der Dichte

 

Die Dichte (hier beim Stab als Masse pro Länge gemeint, nicht pro Volumen!) kann in unserem Modell auf unterschiedliche Weise geändert werden, da die Einzelmasse und der Abstand zum Nachbarn einzeln eingegeben werden können.

a) Längsschwingung

Wir beschränken uns wieder auf drei Werte und beginnen mit den mittleren Werten der obigen drei Sätze:

Die Auswertung ergibt:

fo = f(m)			Funktion	Prüfung
m	T	fo	1/Wu(m)	K=(1/(Wu(m)/fo)
0,5	44,8	0,0223	1,4	63,3
1,0	63,7	0,0157	1,0	63,7
2,0	90,5	0,0110	0,7	64,0

Das Diagramm bestätigt die reziproke Wurzelfunktion:

Wir erhalten also einen Zusammenhang der Form

(m1)    Proportionalität zur reziproken Wurzel der Masse: f_o ~ 1/√m

Das kennen wir schon von der Schwingungsgleichung. Wir haben hier wieder auf eine Anpassung der Größe K an das Diagramm verzichtet (dort reziprok).

Wir prüfen zu unserem Verständnis noch die Änderung der Länge der entspannten Feder, wodurch sowohl die Länge der Kette als auch ihre Dichte verändert wird:

Wir erkennen, dass sich weder Frequenz noch Amplitude ändern, dass lediglich eine geometrische Verschiebung entsteht, denn die Federn kürzerer entspannter Länge haben trotzdem die gleiche Federkonstante behalten. Dieses Problem müssen wir beachten, wenn wir den Vergleich mit einem voluminösen Balken einer gegebenen Dichte und Elastizitätskonstanten ziehen wollen.

Man kann es sogar auf die Spitze treiben und die entspannte Federlänge bei beibehaltener Federkonstante Null setzen, ohne dass sich die Physik ändert:

Diese Länge der entspannten Feder ist also tatsächlich eine intervallskalierte Größe und physikalisch bzgl. der Schwingung irrelevant! (Die rationalskalierte Größe für das Hookesche Gesetz ist die Längen-Änderung!)

Daraus folgt, dass wir in den Gleichungen für die Frequenz die „Länge“ der Federkatte als dimensionslose Anzahl der Kettenglieder zu betrachten haben oder aber auch die Masse der Einzelmasse als „Linienmasse“, also als lineare Massendichte…

 

b) Biegeschwingung

Wir variieren die Einzelmasse in den Spiralfedern bei einem konstanten Abstand (hier jetzt wieder: 50) und erhalten:

lo=	50
m	fo	K=Wu(m)*fo
0,5	0,00019	0,0001344
1	0,000134	0,0001340
2	0,000096	0,0001358

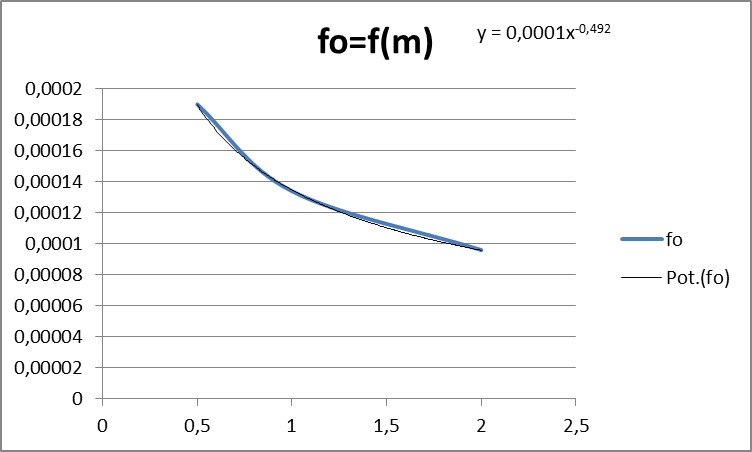
Wir erhalten also einen Zusammenhang der Form

(m2)    Proportionalität zur reziproken Wurzel der Masse: f_o ~ 1/√m

Hier gibt es keinen Unterschied zur Längsschwingung! Die Masse steckt sozusagen in der Dichte drin und hat keine geometrisch explicite Auswirkung in Abhängigkeit von der Schwingungsform.

3. Abhängigkeit von der Elastizitätskonstanten, hier Federkonstante

 

Nach der Untersuchung der Masse sollten wir den Analogieschluss ziehen, dass hier ebenfalls eine Wurzel, aber im Zähler, auftaucht. Aber wir müsse das Modell dediziert prüfen!

a) Längsschwingung

Wiederum drei Werte im Verhältnis jeweils 2/1:

Es fällt sofort ins Auge, dass es die drei Diagramme von oben sind, nur in umgekehrter Reihenfolge. Das Ergebnis ist entsprechend:

fo = f(k)			Funktion	Prüfung
k	T	fo	Wu(k)	K=Wu(k)/fo
3,2	89,5	0,0112	1,8	160,1
6,4	63,7	0,0157	2,5	161,1
12,8	45,3	0,0221	3,6	161,9

Wir erhalten also einen Zusammenhang der Form

(k1)    Proportionalität zur Wurzel der Federkonstante: f_o ~ √k

Das kennen wir schon aus dem Zusammenhang in der Schwingungsgleichung:

(m1) und (k1) ergeben: f_o ~ √(k/m)

(m1) und (k1) und (L1) ergeben: f_o ~ √(k/m)/L

Es erhebt sich nun die Frage, ob es weitere Parameter gibt, die die Frequenz beeinflussen können? Physikalisch sind da noch die äußere Kraft der Erdbeschleunigung (die bekanntermaßen zum Beispiel die Pendelbewegung beeinflusst) und die Zahl der Einspannungen.

b) Biegeschwingung

Die Biegesteifigkeit kg des Stabes ist in der Federkonstanten der Spiralfedern – die, inunserem Modell selbst massebehaftet, zwischen je zwei masselosen Verbindungs-Stäben liegen – versteckt. Wie wirkt sich ihre Änderung – hier Gelenkkonstante genannt – aus? Wir machen wieder zwei Abweichungen vom „Normalfall“ 1 in beide Richtungen mit dem Faktor 2, also die drei Werte

kg = 0,5; 1; 2:

Man erkennt durch Übeung schon auf den ersten Blick, dass sich bei einer Vervierfachung von kg die Frequenz verdoppelt, also eine Wurzelfunktion vorliegen muss. Wir bleiben aber stur bei unseren Hilfsmitteln Tabelle und Diagramm mit Trendlinie:

fo = f(kg)		Funktion	Prüfung
kg	fo	Wu(kg)	K=Wu(kg)/fo
0,5	0,000096	0,707	7365,7
1,0	0,000134	1,000	7462,7
2,0	0,000190	1,414	7443,2

Die Wurzelfunktion ist bestätigt und wir können di ersten drei Messergebnisse wie folgt zusammenfassen:

(L2)   Proportional. zum Quadrat der rezipr. Länge:  fo ~ 1/L²

(m2)    Proportionalität zur reziproken Wurzel der Masse: f_o ~ 1/√m

(kg2)    Proportionalität zur Wurzel der Federkonstante: f_o ~ √kg

f_o ~ 1/L² * √(kg/m)

Es erhebt sich nun auch hier die Frage, ob es weitere Parameter gibt, die die Frequenz beeinflussen können? Physikalisch sind da noch die äußere Kraft der Erdbeschleunigung (die bekanntermaßen zum Beispiel die Pendelbewegung beeinflusst) und die Zahl der Einspannungen.

 

4. Abhängigkeit von der äußeren Kraft, hier durch die Erdbeschleunigung

 

Die Erdbeschleunigung wirkt über die gravitative Masse als Kraft, die die träge Masse beschleunigt, bis die Federkraft gleich groß ist. Die daraus folgende Schwingung kann gedämpft werden und kommt im Gleichgewicht beider Kräfte zur Ruhe. Die Ruhelage selbst, die natürlich elastisch von der Erdbeschleunigung abhängt,  ist aber hier nicht die Frage, sondern nur die Frequenz der Schwingung als solche. Es könnte also durchaus sein, dass der Versuch „negativ“ ausgeht!

a) Längsschwingung

Wir erkennen, dass sich lediglich die Amplitude der Schwingung geändert hat, ordentlich elastisch proportional zur äußeren Kraftänderung beim plötzlichen „Einschalten“ der Erdbeschleunigung.

b) Biegeschwingung

Man erkennt auch hier, dass sich lediglich die Amplitude verdoppelt. Die Formel für die Frequenz bleibt also unverändert.

 

5. Abhängigkeit von der Einspannung

 

Wir ändern die Einspannung in eine beidseitige. Was erwarten wir? Die Welle hat jetzt andere Wege zwischen Einspannung (jeweils Knoten) und Bauch (bisher am Ende, jetzt in der Mitte). Die Frequenz sollte sich also verdoppeln?

a) Längsschwingung

Tatsächlich zählen wir jetzt 12 Schwingungen statt 6 in der gleichen Zeit, also die doppelte Frequenz. Die Amplitude hat sich verkleinert. Wir testen (quasi aus Langeweile für stärker Bilder) das bei einer anderen – stärkeren – Erdbeschleunigung:

Es sieht wirklich ledigleich etwas stärker aus, ändert aber nichts an den Frequenzen und schon gar nicht an ihrem Verhältnis zueinander…

Wir können unsere Untersuchungen hier abbrechen und das Ergebnis diskutieren.

Die Formel, die wir aus den Experimenten gefunden haben, lautet wie oben

f_o ~ √(k/m)/L  oder f_o = K*√(k/m)/L

Die erste Prüfung gilt der Dimension:

1/s = [K] * √((N/m)/(kg/m))/m

1/s = [K] * √((kg*m/(s²*kg/m))/m

1/s = [K] * √(m²/s²)/m = [K]/s

K ist also dimensionslos und kann aus unseren Experimenten bestimmt werden, wenn wir die einsgestellten Werte einsetzen:

Standard-Beispiel aller obigen Tests:

Einspannungszahl E	1
Anzahl der Massen n	40
Einzelmasse m	1
Beschleunigung g	0,4
Federlänge l	25
Federkonstante k	6,4
Dämpfung D	0

Ermittelte Frequenz:

Zweimal kann man die Frequenz ablesen, oben als Quotient von 6 Schwingungen auf  382 s als 0,0157/s oder im Spektrum als 0,0156/s (in der EXCEL-Tabelle kann man das Diagramm mit Hilfe des Mauszeigers für jeden Punkt der Kurve abfragen, hier im Nulldurchgang des ersten Peaks).

Setzen wir also ein in:

f_o *L /√(k/m) = K = 0,0157*40/√(6,4/1)

erhalten wir

K = 0,248 ≈ 1/4

Das liegt im Rahmen unserer Messgenauigkeit ziemlich dicht an 1/4.

Woher kommt das Viertel? Wir haben es mit einer Viertel-Längsschwingung zu tun, wenn wir einen einseitig eingespannten Längsschwinger betrachten. Der beisdseitig eingespannte hätte hier den Faktor 1/2, also die doppelte Frequenz, wie wir oben schon experimentell gemessen haben, denn dort ist es eine halbe räumliche Schwingung.

Jetzt ist also eben der exakten qualitativen (kausalen) Funktion des longitudinal schwingenden Stab-Modells auch noch die quantitative Physik perfekt in Ordnung. Was will man mehr??

 

b) Biegeschwingung

Wir vergleichen wieder die einseitige Einspannung mit der beidseitigen (der  einspannungsfreie Stab würde einfach herunterfallen (auch das muss getestet werden zur Sicherheit, ob das Modell das hergibt!).

Einseitig mit Schwinguns-Strobogramm:

Zweiseitig mit Schwingungs-Strobogramm:

Man erkennt eine sehr deutliche Erhöhung der Frequenz auf etwa das knapp Achtfache! Am Strobogramm erkennt man, dass jetzt eine vierfach verlängerte Biegelinie vorliegt, die obere sozusagen im Wendepunkt endet, die untere aber komplett ist. Stimmt das mit der Theorie überein?

Eine genauere Messung erhält man vielleicht mit 60 Massen, um die diskreten Einspannungen in ihrer Auswirkung herabzusetzen. Da dann die Numerik schon am Anschlag ist, muss man vielleicht die Schwingzeit ablesen und das Verhältnis bilden:

Man kommt auf ein Frequenzverhältnis von etwa 6,7 statt der theoretischen 6,363 und hat sich durch Erhöhung der Gliederzahl also tatsächlich weiter weg bewegt vom Ergebnis „knapp 8“.

Wie sieht nun das Einsetzen aller erhaltenen Zahlen in die erhaltenen Proportionalitäten aus?

f_o ~  √(kg/m)/L²

Hier haben wir eine andere Formel, die auf den ersten Blick so aussieht, als ob die physikalischen Dimensionen (Einheiten) nicht stimmen könnten, da statt 1/L wie im longitudinalen Fall hier jetzt 1/L² erscheint. Wir müssen aber beachten, dass wir statt k (Längsfederkonstante) jetzt kg (Biegefederkonstante) haben, das sich auf die Winkel zwischen den Gliedern bezieht, wodurch der Abstand zwischen ihnen auf einmal eine Rolle spielt, wenn sie ihren Ort senkrecht dazu verändern. Das ist genau die zusätzliche Lämgeneinheit!

Nehmen wir also wieder das Standardbeispiel aller obigen Tests:

Zum Vergleich noch ein Spektrum mit cos statt sin generiert:

Die im Original abgelesene Frequenz fo ist in beiden Fällen 0,000134 Hz (links im Nulldurchgang, rechts im negativen Peak), 20 Glieder im Abstand 50 mit einer Gelenkkonstante (Biegesteifigkeit pro Länge) von 1/50 und einer Masse von je 1. (Natürlich kürzt sich die Länge ein halbes Mal – unter der Wurzel! – raus, wenn man die extreme Geometrie eines dünnen Stabes statt eines Balkens mit echtem Flächenträgheitsmoment nimmt.)

L²*f_o / √(kg/m) = K

(20*50)² * 0,000134 * √(1/(50*1)) = 19 = K

Was sagt uns das?

Die Größe kg haben wir so verwendet, dass sie eine Beschleunigung senkrecht zum Stab bewirkt, und zwar in Abhängigkeit vom Winkel. Der Winkel wird dabei nicht in Grad, sondern im Bogenmaß gemessen. Es bedeutet also, dass bei einem Winkel von 1 (etwa 57,3°) ein Drehmoment von 1 (Nm) entsteht. In einem Abstand von 50 (m) erzeugt das eine Kraft von 1/50 (N). Diese entspricht nun physikalisch dem, was wir bei der longitudinalen Schwingung angesetzt haben. Sie bewirkt eine Geschwindigkeitsänderung der Masse 1 (kg) von 1/50 (m/s) in einer Zeit von 1 (s). Dadurch stellen sich neue Winkel ein usw. usf. Mehrere Nachbarn wirken dabei zusammen, um für eine Masse die Gesamtkraft (incl. Erdbeschleunigung) und damit die Gesamtbeschleunigung zu superponieren, was im Code dann (ohne Winkelnäherung atn(x)=x) so aussieht:

yb(j) = 1 / em * (kg * (-1 / 2 * Atn((y(j) – 2 * y(j – 1) + y(j – 2)) / L) + Atn((y(j + 1) – 2 * y(j) + y(j – 1)) / L) – 1 / 2 * Atn((y(j + 2) – 2 * y(j + 1) + y(j)) / L)) – G)

In der Theorie gibt es den Faktor 3,5 zu den elastischen und geometrischen  Größen, wenn man die Kreisfrequenz wo = 2*pi*fo des einseitig eingespannten Balkens berechnen will.

2*pi*3,5 = 22 liegt vertretbar dicht an K=19 (etwa 15%), wenn man auch die Ungenauigkeiten der Frequenzverhältnisse von beidseitig und einseitig eingespanntem Balken (Stab) betrachtet, die je nach unseren Messungen für unterschiedliche Parameter zwischen 6,7 und 8,5 und damit ebenfalls bei mehr als +- 10% von ihrem Mittelwert lagen und mehr noch entfernt vom Theoriewert 6,36.

Fazit: Beim Biegen wird es etwas komplizierter mit der Diskretisierung, weshalb die numerische Rechnung (bei der Nutzung sehr einfacher Mittel wie einem alten PC und EXCEL/VBA) nicht so genau an die analytischen Ergebnisse herankommt wie bei der longitudinalen Schwingung. Die qualitativen Effekte sind aber auch bei der Biegeschwingung ALLE richtig aufgetreten und in quantitativer Hinsicht hinreichend, wenn man damit keine aus der Baustatik kommenden Sicherheitsbestimmungen befriedigen muss.