Joachim Adolphi

2.4.1.1.2.2 Biegeschwingung des Stabes

• Joachim Adolphi
• Samstag, 14. Oktober 2023
• Sonntag, 29. Oktober 2023
• Biegeschwingung, Oberton, Schwingung, Stab

Ob es gelingt, die nichtharmonischen Biege-Schwingungen eines Stabes einfach zu modellieren?

Im Unterschied zu den drei Fällen

– Longitudinalschwingung des Stabes und der Luftsäule

– Transversalschwingung der Saite

– Torsionsschwingung des Stabes

die durch Analogie-Schluss alle in 2.4.1.1.2.1 behandelt worden sind, müssen wir nun zuerst die Besonderheiten der Biegeschwingung herausarbeiten.

Warum versagt hier der Analogie-Schluss, der doch nahelegt, dass anstelle von Abständen nur einfach Winkel gesetzt werden müssen und die physikalischen Größen zu ersetzen sind: Masse durch Trägheitsmoment, Kraft durch Drehmoment, Federkonstante der Schraubenfeder durch die der Spiralfeder. Dann wirkt wieder jedes elastische Element auf die beiden Nachbarn, es entstehen Wellen und schließlich stehende Wellen und der stabile Schwingungszustand, dem man Obertöne zu einem Grundton zuordnen kann, ist fertig.

Genau das trifft alles auf die Torsionsschwingung zu. Dort nämlich bezieht sich alles auf die gleiche Drehachse wie oben alles auf die gleiche Längsbewegung entlang einer Geraden.

Jetzt aber hat jedes Element seine eigene Achse (wenn diese auch parallel zueinender sein mögen!), ist aber seitlich versetzt zum Nachbarn. Die auf diese Weise miteinander verbundenen Bewegungen müssen eigentlich jeweils in andere (zudem noch zueinander bewegte) Bezugssysteme transformiert werden. Es wäre also ein Wunder, wenn das NICHT zu anderen Lösungen führen würde!

Fangen wir also wieder ganz vorsichtig an und bauen das Modell schrittweise auf. Schon beim Mehrfach-Pendel hat man gesehen, dass das schnell „chaotisch“ wirken kann, obwohl es streng determiniert ist (siehe Doppelpendel unter 2.8.6.1).

Für kleine Auslenkungen können wir wieder die Winkelfunktionen Sinus oder Tangens ihrem Argument gleichsetzen und davon ausgehen, dass sich alle Massen nur senkrecht zum Stab bewegen (eine überhöhte Darstellung im Diagramm ist dann eine reine Sache der Anschaulichkeit!). Unter diesen Umständen vereinfachen sich die Wechselwirkungen benachbarter diskretisierter Biege-Elemente deutlich. Dann müssen wir nur auf die Erhaltungssätze von Kraft und Drehmoment achten und können folgende Beziehung für die „inneren“ Elemente aufstellen:

– Kraft auf Element i ergibt sich aus seinem eigenen Drehmoment und den jeweils halben der beiden Nachbarn i-1 und i+1, jeweils dividiert durch den konstanten Elementabstand

– das jeweilige Drehmoment (das „eigene“sowie das der Nachbarn!) ergibt sich dabei proportional aus dem Winkel der Richtungsänderung der beiden Verbindungslinien zu den weiteren beiden Nachbarelementen

– die Randelemente müssen deshalb natürlich gesondert behandelt werden

– außerdem ist es ganz wichtig, welche Art der EINSPANNUNG des Stabes vorliegt, weil das Randbedingungen für die Integration liefert

– aus den Kräften ergeben sich wieder die Geschwindigkeits- und Orts-Änderungen der Elemente durch doppelte Integration

Neu ist hier nun also die gewichtete Einbeziehung der Winkel der nächsten und also der Porision der übernächsten Nachbarn in die Kraftwirkung (siehe Anhang von 4.2.1.1.2!), was einer geometrischen Differentiation entspricht, die über die der Wellengleichung hinausgeht, weil hier die Kraft selbst schon von der geometrischen Krümmung abhängt und nicht nur einfach vom Abstand von der lokalen Gleichgewichtslage. (Dort, bei der einfachen Welle, ist die geometrische Krümmung – zweite Ortsableitung der Form – der zweiten Zeitableitung des Ortes – der Beschleunigung – proportional: je stärker die Krümmung, desto stärker die rücktreibende Kraft, desto weiter aber auch der Weg. Das sind die Eigenschaften der reellen Sinus- oder Cosinusfunktion in Ort UND Zeit, also einer Welle.)

A) EINSEITIG EINGESPANNTER STAB

Die ersten Testergebnisse mit einem ersten festen Element (fest sind Ort und Verbindungsrichtung zum Gestell), 7 beweglichen inneren Elementen und einem Schluss-Element bringen, bezogen auf die Grobheit dieses Modells, schon erstaunliche Ergebnisse aus einer einfachen EXCEL-Tabelle:

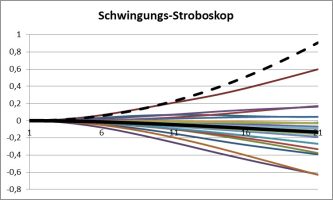
Mit experimentell ermittelten ruhenden Startpositionen (ganz links in den Diagrammen an der Ordinaten-Achse abzulesen) können Schwingungen erzeugt werden, die stehenden Wellen sehr nahe kommen und von 0 bis 3 Knoten enthalten. Die Frequenzverhältnisse sind denen aus der Theorie schon erstaunlich nahe:

In den Diagrammen sind die Schwingungen aller Massen im Zeitablauf dargestellt, nicht räumlich! (Bei 0 Knoten schwingt der gesamte Stab bis zu seinem freien Ende hin und her, bei einem Knoten macht er bis dahin abwechselnd nach oben und unten einen Bauch bis zum Knoten und schleudert seine kurze Spitze – rot dargestellt – hinter dem Knoten in die Gegenrichtung hin und her. Bei zwei Knoten sind stets entgegengesetzte Bäuche vorhanden und hinter dem zweite Knoten schleuidert wieder die Spitze usw. usf.) Man soll den synchronisierten Nulldurchgang erkennen können. Dass bei so geringer Massenanzehl lauter Oberwellen dicht an der Molekülschwingung dabei sind, sollte nach dem Studium im vorigen Abschnitt wirklich nicht verwundern!

Die Gegenüberstellung der Frequenzverhältnisse sieht so aus (bezogen auf die Grundfrequenz):

	Anregung Grundschw
Mode	f	f/f0	Theorie **)
1	0,0023675	1	1
2	0,01510	6,378	6,27
3	0,04220	17,82	17,57
4	0,08135	34,36	34,37

(Mit 8 inneren Massen am Ende 3 Knoten und 4 Bäuche darstellen zu wollen ist schon sehr abenteuerlich: Man befindet sich schon im Bereich der „Molekülschwingungen“, nämlich benachbarte Massen schwingen gegeneinander! So gesehen ist die Genauigkeit der Ergebnisse sensationell!)

Nun kann also an eine Programmierung mit wieder etwas mehr diskretisierten Einzel-Massen gegangen werden!

Das Programm ist fertig, der erste Test positiv, es sollten ja wenigstens annähernd die gleichen Bilder erzeugt werden können. Das klappt (aber erst nach der üblicherweise notwendigen Korrektur von Leichtsinnsfehlern…):

Der zweite Test ist auch erfolgreich, nämlich das Hinzufügen von Schwerkraft und Dämpfung zur Erzeugung einer sich selbst einstellenden Biegelinie durch die gleich verteilte Eigenmasse, jetzt mit 21 Massen:

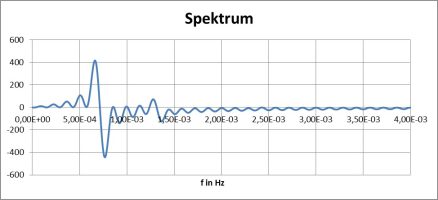
Man sieht gut, dass es sich um die Grundschwingung ohne Knoten (außer der linken Einspannung) handelt. Man sieht auch, dass es einen geringen Oberwellenanteil gibt, der in einer Fourier-Analyse ermittelt werden sollte (sind es die oben erwähnten Obertöne?):

Das Spektrum zeigt, das das „Gezappel“ nicht ein numerischer Artefakt, sondern reine Physik der Schwingung und der Wellen ist, denn auch bei genau getroffener Ausgangslage (Anregung mit der Biegelinie des Balkens!) ergibt sich der der gleiche erste Oberton im Verhältnis zur Grundschwingung (bei 40.000 zeitlichen Stützstellen und etwas anderen elastischen Parametern…):

Wir prüfen das genauer zuerst „rein“ und dann bei Zusatzkräften (Schwerkraft) und Hindernissen (Dämpfung), und zwar wieder bei 21 Massen.

Man erkennt hier sogar neben dem ersten Oberton (6,55 statt 6,27-facher Grundton) auch den nächsthöheren Oberton mit 2 Knoten (jetzt wurde die 10. Masse von 21 untersucht) bei der etwa 18,1-fachen Grundfrequenz(statt 17,6 in der Theorie)! Also auch dieses „verzappelte Gezappel“ ist echt!

Und sogar im durch die Schwerkraft verzerrten und durch Dämpfung beendeten Schwingungsbild sind alle drei Moden noch an den richtigen Stellen zu erkennen.

Noch der Versuch mit 41 Massen und der FA bei Masse 20:

Der dritte Oberton (nun also vier Moden!) erscheint bei der 35,4 statt 34,4-fachen Grundfrequenz. Dass alle Töne etwas zu hoch sind, weist darauf hin, dass entweder die Einspannungskonstruktion durch die Diskretisierung unglücklich gewählt ist oder der Grundton genauer ermittelt werden sollte.

So ist es, denn bei einer Spreizung der FA ergab sich ein hunterfach genauerer Grundton und damit folgendes Ergebnis für das entwickelte Modell:

Modell-Praxis/Theorie:     1/1    6,38/6,27   17,82/17,57   34,36/34,37

(Der letzte Wert ist sicher zufällig derart exakt, allerdings liegt hier auch die größte Anzahl von Einzelschwingungen vor, so dass die FA grundsätzlich genauer wird…)

Das Modell funktioniert also und kann für weitere Untersuchungen ausgebaut werden:

z.B.: Kann man die Obertöne einfach direkt anregen?

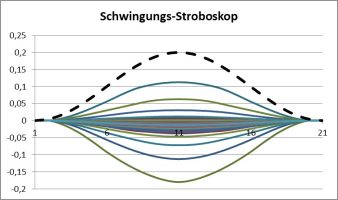
Ich habe zwei Versuche gemacht: Zuerst mit einer quadratischen Funktion, die linear korrigiert ist:

y = a*(x² – 0,788x)  (a ist die „Amplitude“)

Die gestrichelte Startlinie startet an der Einspannung natürlich zu steil!

Dann in einem zweiten Versuch mit einer „rein optisch“ besser angepassten:

y = a*(x^4 – 0,7 * x^2)

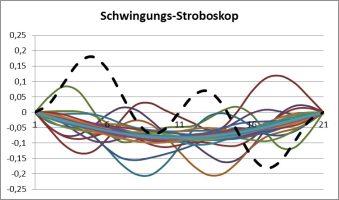
Jetzt braucht die Startlinie etwas zu lange, um sich  von der Mitte zu entfernen. Trotzdem erkennt man, dass die Spektren sehr ähnlich sind und sowohl die erwarteten Moden zeigen als auch eine zusätzliche Serie mit jeweils dazwischen liegenden Frequenzen. Bei den linken Diagrmmen des Zeitablaufs der Schwingungen erkennt man an den Farben das Gegenschwingen von Rumpf und Schwanz des Mode-2-„Fisches“ sehr gut! In einer „verlangsamten“ Darstellung natürlich noch besser:

Zum allerletzten Schluss des Themas „Biegeschwingung des einseitig eingespannten Stabs“ noch die beiden Anregungs-Varianten für den ersten Oberton eines 59-Massen-Stabes:

Wie man sieht, kann man nun die einzelnen Massen kaum noch optisch trennen. Um das Spektrum zu schärfen, wird noch einmal die Taktzahl von 10.000 auf 40.000 erhöht, und man kann die oberen Peaks nun wirklich deutlicher sehen:

	Anregung  1. OT
Mode	f	f/f1	Theorie
1	0,0015100	0,18171	0,15949
2	0,00831	1	1
3	0,02100	2,52708	2,80223
4	0,037	4,45247	5,48166

Die Rechenzeit wird nun aber schon etwas belästigend lang…

Auch für die Grundschwingung bringt das eine gewisse Schärfung, wenn man 59 Massen und 40.000 Takte nimmt:

Es fällt auf, dass die Oberschwingung mit 2 Knoten schwach besetzt ist, die mit 3 wieder besser. Das kann an der nicht optimalen (rein quadratischen) Ausgangsfunktion liegen. Trotzdem ergeben sich gute Schwingungsverhältnisse (die Frequenzwerte sind einem gespreizten Spektrum und der Tabelle entnommen und teilweise interpoliert):

Grund  59m 40.000T
f/Hz	Verhä.	Theorie
0,00011516	1	1
0,000725	6,29559	6,27
0,00206	17,8882	17,57
0,00396	34,3869	34,37
0,00652	56,6169	56,84
0,00968	84,057	84,91
0,01798	156,131	157,9

(vor dem letzten Wert hätte noch 118,6 liegen sollen…)

Zum Schluss lassen wir noch den geraden Stab durch die Schwerkraft in die Biegelinie, die aus der Statik bekannt ist,  gedämpft einschwingen:

B) FREI SCHWINGENDER STAB

(ohne jegliche Einspannung, also zum Beispiel im Fluge…)

Das oben genutzte VBA-Programm muss also ledoglich in den Randebdingungen der ersten beiden Massen verändert werden. Wir beginnen mit einer symmetrischen Anfangsbedingung, biegen den 59-er Stab also mit einer halben Sinuswelle und lassen dann los und vergleichen wieder mit der Theorie:

Mode	f	f/f1	Theorie
1	0,000724	1	1,00
2		0	2,76
3	0,00392	5,41436	5,41
4		0	8,94
5	0,0096	13,2597	13,17

Wir erkennen, dass Obertöne fehlen, offenbar sind das hier nur die symmetrischen Schwingungsbilder, die unsymmtrischen fehlen wegen der symmetrisch erfolgte Anregung.

Es ist ein sehr schönes Gefühl, wenn man erlebt, dass das gerade erst entworfene Modell so gut funktioniert!

Wir erkennen aber auch, dass die Schwingung geometrisch nicht um die Null-Linie erfolgt. Das ist spannend. Offenbar haben wir mit dem Schwerpunkt des Systems in den Anfangsbedingungen gepfuscht. Jetzt korrigieren wir das:

Jetzt sind die Schwingungen um die Null-Lage positioniert (der Schwerpunkt der Sinus-Halbwelle liegt bei 2/pi=0,637), aber eben einfach parallel verschoben, was ja kein Wunder ist, wenn wir mit einer physikalisch unwesentlich skalierten Achse arbeiten, die wegen fehlender räumlicher Randbedingungen ihre Intervallskaliertheit natürlich offenbaren muss. Aber Ordnung muss eben sein… Übrigens ist die FA jetzt an Masse 25 von 59 vorgenommen worden und zeigt nur noch die Grundschwingung… Wie sieht es bei Masse 1 oder Masse 7 (dort zeigen sich leichte Splittungen im Strobogramm)  aus? Genauso…

Die Knoten dieser Schwingung liegen übrigens bei

1/pi*arcsin(2/pi) = 22% der Gesamtlänge von vorn und hinten (siehe Bemerkung ganz unten *).

Eine unsymmetrische Anregung müsste bei einem freien Stab allerdings zu einer Rotation führen, hat man so im Gefühl. Wir testen das einfach aus:

Upps! Der Gedanke wahr wieder fahrlässig doppelt falsch: Die Viertel-Sinus-Biegung ist zwar nicht richtig symmetrisch, hat aber dennoch 2 Knoten zur Folge, und eine Rotation bleibt auch aus, denn ein äußeres Drehmoment haben wir schließlich nicht angelegt!

Probieren wir also mit einem Drei-Viertel-Sinus:

Obwohl das Stroboskop-Bild einen dritten Bauch andeutet, ist der im Spektrum nicht zu sehen. Liegt seine Frequenz nicht an der erwarteten Stelle oder ist die Messung zu ungenau? Bei höheren Frequenzen treten noch zwei weitere Mini-Peaks auf (23,1 und 39,2-fache Grundfrequenz):

Probieren wir noch die komplette Sinus-Welle:

Das geht nicht mit rechten Dingen zu…

Und wirklich: Ich bin oberflächlich, denn die FA fand genau an der mittleren Masse 30/59 statt, wo es bei einem Drittel, also bei Masse 20 von 59, angebracht wäre! Hier nun das doch wirklich zu erwartende Ergebnis bei 20/59:

Hier sind die ungeraden Knoten nun endlich gut zu sehen!

Dafür fehlen die geraden etwas, deshalb eine weitere Änderung der analysierten Masse: Bei z.B. 18/59 und einer Anregung mit dem Drei-Viertel-Sinus sollten also alle zu sehen sein!

Und tatsächlich ist das Spektrum nun komplett in einer einzigen Analyse zu sehen. Wir sind also am Zwischenziel angelangt.

Damit ist nun unsere ergänzte Tabelle tatsächlich praktisch für die ersten fünf (auch theoretisch in der Literatur – WIKI – angeführten) Modi vorgeführt:

Mode	f	f/f1	Theorie
1	0,000724	1	1,00
2	0,002000	2,76243	2,76
3	0,003920	5,41436	5,41
4	0,006500	8,9779	8,94
5	0,009600	13,2597	13,34
7	0,0167	23,0663	24,81
9	0,0284	39,2265	39,81

Uff, geschafft, mit Umwegen zwar, aber das ist normal beim Basteln!

C) SCHWINGENDER STAB mit 2 gelenkigen BEFESTIGUNGEN

(auch an 2 inneren Stellen)

Das ist nicht exakt das Xylophon, denn dort liegt der Stab nur auf, hier aber sind zwei Punkte (die etwa den Auflagern des Xylophons ensprechen (siehe *) ganz unten) befestigt. Eine erster Test ergibt noch unverständliche Peaks im Spektrum:

Es ist das mittlere Fünftel des Stabes rechteckig angeregt, die festen Auflager liegen etwa 22% der Länge von den Enden weg.

Wir sollten also eine andere Anregung überlegen. Das ist didaktisch ganz interessant, allerdings wird in der Literatur nicht zwischen leicht aufgelegt und punktförmig eingespannt unterschieden, was ja richtig ist, denn es gibt hier keine Randbedingung für die erste Ableitung nach dem Ort, also für den Winkel in der Einspannung. (Aber eine Xylophon-Platte darf ein wenig nach oben springen…)

Und doch taucht hier eine neue Mode auf, die nach Erklärung schreit:

Das Strobogramm ist wahrscheinlich zufällig so gruppiert, das prüfen wir gleich. Was aber macht die schwache Mode mit der 1,82-fachen Grundfrequenz (die unverändert ist)? Gibt es da eine Reflexions-Mode?

Offenbar ja. Die beiden ersten Frequenzen sind wieder da, und weiter oben noch zwei „Neue“. Das Strobogramm sieht jetzt „normal“ aus, weil die Taktzeit von 0,7 auf 0,69s verkürzt worden ist und diese zufällige Schwebung verschwinden konnte. Da wir bei nur 59 Massen die Auflager nicht so exakt setzen können, wie die Sinuslinie es vorschreibt, werden wir offenbar die „Dreckeffekte“ nicht wegbekommen. Wir können aber versuchen, sie durch größere Abweichungen zu verstärken:

Und tatsächlich: Eine unsymmetrisch nach innen gerückte Auflage macht das Treiben verrückt, weil wir absolut festgelegt haben, dass in den Einspannungen ein Knoten sein MUSS, und es entstehen neue Reflexions-Moden (die man bei einem Xylophon wohl vermeiden will, weshalb alle Auflegen immer relativ locker sind; allerdings liegen die Fremd-Moden so hoch, dass sie wohl noicht zu hören sind…)

Auch hier ein gedämpftes Einschwingen eines geraden Stabes auf die Biegelinie mit Schwerkraft mit unterschiedlicher Dämpfung und Zeittakt:

Sind die gelenkigen Lager ganz außen, so kann man bei einer sinusförmigen Anregung eine reine Mode (Grundschwingung) erzeugen:

Ändert man die Anregung symmetrisch, erscheinen neue Moden (gerade Glieder einer quadratischen Frequenz-Folge):

Wählt man nun noch eine unsymmetrische Anregung, wird der Satz durch die ungeraden Glieder einer quadratischen Frequenz-Folge komplettiert:

Hier wieder der Vergleich mit der Theorie:

Mode	f	f/f1	Theorie
1	1,8	1	1,00
2	7,8	4,33	4,00
3	17,2	9,55	9,00
4	30,4	16,89	16,00
5	46,1	25,61	25,00
6	65,8	36,56	36,00
7	86,9	48,28	49,00
8	110,2	61,22	64,00

Die Ungenauigkeiten liegen evtl. an der schlechten Ermittlung der Grundfrequenz und der zu geringen Anzahl diskretisierter Massen (hier nur 21).

D) BEIDSEITIG FEST EINGESPANNTER STAB

Im Gegensatz zum vorigen Spezialfall ist jetzt die Einspannung nicht nur ortsfest, sondern auch winkelfest, weshalb also die Orte der jeweils beiden Randmassen fixiert sein müssen.

Wir beginnen wieder symmetrisch:

Selten ist eine so markante Änderung des  Spektrums zu sehen!

Nun die unsymmetrischen etwas unsanft dazu:

Die Auswertung zeigt im Vergleich mit der Theorie bei den höheren Frequenzen wieder einen Mismatch wegen der geringen Massenzahl (die jeweils beiden örtlich fixierten – Anstieg muss Null sein! – numerisch diskretisierten  Randmassen werden „relativ wichtiger“, je weniger Massen pro Wellenbauch vorhanden sind und schnüren diese Bäuche ein, weshalb die Frequenz höher wird – ein wenig spielt das auch bei den außen gelenkig gelagerten Stäben mit, wo jeweils nur eine Masse fixiert ist) :

Mode	f	f/f1	Theorie **)
1	0,00485	1	1
2	0,0136	2,80412	2,75658
3	0,02625	5,41237	5,4044
4	0,0428	8,82474	8,93311
5	0,0628	12,9485	13,3445
6	0,0856	17,6495	18,6382
7	0,1104	22,7629	24,8142
8	0,1368	28,2062	31,8724
9	0,1634	33,6907	39,813
10	0,1908	39,3402	48,6358

Das sind übrigens die gleichen Frequenz-Verhältnisse wie beim freien Stab, was an sich schon spannend ist. Man erkennt, dass dort (siehe oben!) ein paar Moden fehlen. Hier hätten noch mehr ermittelt werden können, wenn der Frequenzbereich der FA erweitert worden wäre. Bei den festgestellten Fehlern des groben Modells wäre das aber physikalisch unsinnig…

Will man die Frequenz eines Plättchens verringern, kann man im einseitig eingespannten „Balken“ am Ende eine Zusatzplatte anbringen. Das soll jetzt in unserem Modell umgesetzt werden. Ich bin gespannt:

E) EINSEITIG FEST EINGESPANNTER STAB MIT ZUSATZMASSE

Die Größe dieser Masse soll variabel sein. Wir beginnen zum Vergleich wieder ohne Zusatzmasse und ohne Erdbeschleunigung (oben wurde eine Schwere-Biegelinie als Endzustand nach geeigneter Dämpfung erlangt, jetzt wird die Dämpfung zurückgefahren und die äußere Kraft weggelassen, um den musikalischen Aspekt in den Vordergrund zu stellen).

Ein schwacher Oberton ist wieder zu „hören“, weil die Anregung nicht genau der Biegelinie entspricht. Auch wenn das der Fall ist, ist wiederum der Einfluss der Kürze der Modell-Kette so groß, dass man keine obertonfreie Schwingung hinbekommt:

Nun also schrittweise eine schwerer werdende Zusatzmasse ans Ende hängen:

Hier ist nun (teilweise überraschend!) folgendes festzustellen:

Erwartungsgemäß sinkt die Grundfrequenz stark ab, wenn die schwerer werdende Masse am Ende wächst. Die Grundschwingung wirkt immer „harmonischer“ und geglätteter, je schwerer die Endmasse wird. Die erste Oberschwingung aber ändert ihr Verhältnis zur Grundschwingung stark, weil sie ja offensichtlich die Endmasse nicht so weit mitbewegen muss, sondern „im Inneren“ des Stabes sich austoben kann. Bei den nächsten Moden könnte das noch stärker ausgeprägt sein, was hier aber nicht untersucht worden ist, denn der Frequenzbereich des Diagramms war so schon relativ unglücklich für höhere Genauigkeiten der Grundschwingung, aber alles sollte eben einfacher vergleichbar sein. Auch die geringe Anzahl der Grundschwingungen hat die Satelliten des Spektrums relativ groß werden lassen, aber das wichtigste ist klar zu erkennen: Mit einer Endmasse an der schwingenden Zunge können wir schnell tiefere Töne erzeugen, ohne die Zunge sehr lang werden lassen zu müssen.

Man sieht das übrigens in den „Locken“ des Zeitablaufes der Schwingungen deutlich, dass ihre Zahl pro Halbwelle zunimmt, während ihre „Breite“ (d.h. Schwingzeit) im Diagramm nur wenig zunimmt.

Hier das „excelperimentell“ ermittelte Diagramm des Zusammenhangs zwischen der Frequenzentwicklung und der Zusatzmasse:

Das linke Diagramm passt sehr gut mit einem von Prof. Wandinger von der Hochschule München (siehe **)!) zusammen, wobei dort ein Parameter aufgeführt ist, der die Wurzel aus der Frequenz enthält. Zum Vergleich habe ich aus meinem Diagramm ebenfalls die Wurzel gezogen und die Abszisse gekürzt:

(Man beachte beim Vergleich, dass im rechten Diagramm die Ordinate nicht bei Null beginnt und die Frequenzerniedrigung der Grundschwingung dadurch zu stark erscheint!)

Mit diesem musikalisch-instrumententechnisch relevanten Beispiel machen wir vorläufig Schluss. Das Spielen mit dem Modell ist sehr spannend, aber auch ein wenig zeitaufwändig.

Es sieht aus, als ob wir unser Ziel erreicht haben:

Wir haben die Eigenfrequenzen eines freien oder unterschiedlich eingespannten oder belasteten Stabes modelliert und vernünftige Ergebnisse erzielt und dabei viel Grundsätzliches wiederholt sowie neu kapiert, vor allem, worin der Unterschied zwischen der Biegeschwingung und den anderen besteht. (Man versteht jetzt auch, warum man bei der schwingenden Saite betonen muss, dass reine Längsspannung OHNE Biegemoment angesetzt wird.)

Bei Gelegenheit kann man weitere Einspannungs-Varianten für die Biegeschwingung untersuchen oder auch andere Zusatzmassen hinzufügen (u.a. zur Frequenzerniedrigung. Also vielleicht bis bald wieder?…)

*): Die Auflager für das Xylophon verstehe ich so, dass dort der Nulldurchgang einer halben Sinus-Welle wäre, wenn man diese vorher um ihren Schwerpunkt 2/pi absenkt (so ähnlich, wie oben mit einer halben Welle angeregt worden ist):

1/pi*arcsin(2/pi)

ist  21,97 %.

**): Eine gute Theorie-Seite, nach der hier die theoretischen Vergleichs-Werte berechnet worden sind, wäre z.B.:

https://wandinger.userweb.mwn.de/LA_Elastodynamik_2/index.html

 

Kommentare