Darstellung von räumlichen Zusammenhängen
„Struktur“ erinnert an einen Zusammenhang mit dem Raum.
Wie stellt man Raum dar? In der Schule haben wir uns in der Geometrie vor allem mit dem zweidimensionalen Raum beschäftigt und haben ihm zwei Achsen gegeben, die x- und die y-Achse. Die stehen immer senkrecht aufeinander. Warum eigentlich?
Machen wir einen indirekten Beweis: Stünden sie nicht senkrecht aufeinander, könnte man einen Betrag in der einen Achsrichtung durch einen in der anderen anteilig ausdrücken. Im hexagonalen Kristallsystem macht man das mitunter so, was aber zur Folge hat, dass es eine innere Beziehung zwischen der drei Achsen der hexagonalen Ebene gibt, womit ihre gegenseitige Unabhängigkeit aufgehoben ist.
Natürlich kann man zwei Achsen im Zweidimensionalen definieren, die nicht senkrecht aufeinander stehen, dann sind aber die Symmetriebeziehungen sehr kompliziert, wenn man nicht auch alle Winkel neu definiert und alle vektoriellen Beziehungen. Das „orthogonale“ System hat also viele Vorzüge.
Und doch kann man die Ebene auch ganz anders strukturieren: mit Polarkoordinaten (Winkel zu einer Bezugsrichtung und Abstand zum Ursprung). Auch hier kann man keine der beiden durch die andere ausdrücken. Das ist sinnvoll für alle Arten der Drehbewegung oder für alle Arten der Abhängigkeit vom Abstand von einem einzigen Zentrum. In der Kristallografie aber, wo es um „Translationsinvarianz“ der Struktur (Zellen) geht, sind nun einmal Achsen bequem, die den Zellen anliegen.
Der Orthogonalitätsbegriff wird aber auch abstrakter verwendet: Wenn zwei Funktionen eines Systems nicht durcheinander ausgedrückt werden können, nennt man das System orthogonal. Dann gibt es analog zu den Vektoren ein Skalarprodukt (hier in Integralform), das Null ist, und ein Vektorprodukt, das im Falle der Normiertheit des Systems 1 ist. Solche Funtionen benutzt man zur Reihenentwicklung (auch in der Akustik -> Musik).
Es ist also wichtig, Schulstoff zu wiederholen:
- Darstellung einer Ebene im Raum
- Darstellung einer Geraden in der Ebene und im Raum
- Beziehung zwischen der Normalen einer Ebene und dieser selbst
- Winkel zwischen zwei Ebenen
- Schnittgerade zweier Ebenen (Kante eines Kristalls)
- Schnittpunkt dreier Ebenen (Ecke eines Kristalls)
- Schnittpunkt zweier Geraden in der Ebene und im Raum (falls nicht windschief)
Und dann kommt noch etwas hinzu:
Häufig ist es sinnvoll, zwischen zwei Koordinatensystemen zu wechseln. Das nennt man Transformation. Manchmal verändert sich nur der Satz an Koordinaten selbst (Mathematik, Geometrie: zum Beispiel räumliche Drehung räumlicher Objekte), oft aber ändern sich auch physikalische Größen (zum Beispiel bei der Galilei-Transformation der Bewegung schwerer Massen). Die Anpassung der Koordinaten an die Gegebenheiten erleichtern dann die konkrete Arbeit, besonders wenn eine Invarianz des Problems gegen entsprechende Transformationen besteht.
Handelt es sich lediglich um eine geometrische Transformation, wird auch gern von „Abbildung“ gesprochen. Im Grunde ist jede „Funktion“ eine Abbildung. Spezielle Abbildungen sind die „Projektionen“, bei denen es sich sehr oft um die Verminderung der Dimensionalität handelt, zum Beispiel wenn eine dreidimensionale Realtität auf eine zweidimensionale „Bildfläche“ zu projizieren ist.
Da solche Sachen alle überall nachlesbar sind, verzichten wir hier auf genauere Darlegung. Hier gilt wie so oft: Erst durch Übung und damit Gewöhnung lernt man die Vorzüge eines Verfahrens wie der Transformation schätzen.
Ein kleines Beispiel sei angeführt:
Bei der Programmierung der Darstellung dreidimensionaler Drehungen dreidimensionaler Objekte auf einem zweidimensionalen Bildschirm muss man sich entscheiden, welche Bedienelemente man verwenden will. Hier eine Gegenüberstellung zweier Programme, meines eigenen für kristallografische Darstellungen und des Programms SHAPE (http://www.shapesoftware.com).
Vergleich Adolphi <> SHAPE
Adolphi
In meinem Kristall-Programm kann man mit der Maus die Objekte im Raum (stereoskopisch betrachtbare Objekt-Paare) mit einer (der linken) Maustaste drehen. Dazu werden die Koordinaten des Mauszeigers abgefragt und komplett auf seine Startposition bezogen:
– waagerechte Bewegungskomponente ergibt Drehung um aktuelle senkrechte Achse
– senkrechte Bewegungskomponente ergibt Drehung um aktuelle waagerechte Achse
– Entfernungs-Komponenten vom Startpunkt der Maus-Zeiger-Bewegung ergeben beide Drehwinkel
Vorteile:
– Reproduzierbarkeit durch umkehrbar eindeutigen Zusammenhang von relativer Mausposition und Drehzustand
– rechte Maustaste bleibt für Formen-Übergangs-Zustand frei
Nachteile:
– keine Addierbarkeit der Mausaktionen
– keine dritte Drehungsachse (Blickrichtung), umständliche Ersatzdrehungen um die beiden anderen Achsen erforderlich
Rechnerische Umsetzung:
relative Mausposition ergibt
– über den Winkel die Richtung des Einheitsvektors der Drehachse (liegt somit immer in der Bildebene!)
– über den Abstand den Winkel der Drehung um diese Achse
SHAPE
Im Programm SHAPE haben beide Maustasten dieselbe Funktion. Es werden ebenfalls die Koordinaten des Mauszeigers abgefragt und eingeschränkt auf seine Startposition bezogen:
– waagerechte Bewegungskomponente ergibt Drehung um aktuelle senkrechte Achse
– senkrechte Bewegungskomponente ergibt Drehung um aktuelle waagerechte Achse
– Entfernungs-Komponenten vom Startpunkt der Maus-Zeiger-Bewegung ergeben beide Drehwinkel
– im linken Bearbeitungsbereich ändert sich die senkrechte Mausbewegungs-Komponente zur Erfassung der Drehung um die Blickachse (Mauszeiger ändert Gestalt!)
Vorteile:
– Addierbarkeit der Maus-Bewegungen
– dritte Achse durch Sonderbereich bedienbar
Nachteile:
– keine Reproduzierbarkeit
– Formänderung nur durch weitere Bedienelemente einstellbar
– aktuelles Achsenkreuz muss zusätzlich angezeigt werden, um Drehungen schrittweise und intuitiv rückgängig machen zu können
Die Umsetzung erfolgt bei mir also über die Abfrage der Koordinaten der Mausposition beim Tastendruck und dann ständig bei der weiteren Mausbewegung. Die daraus berechneten Komponenten der Drehachse und der Drehwinkel werden für jeden der abzubildenden Punkte samt deren Koordinaten in die Drehmatrix (studiere Quellen im Internet!) eingesetzt und die neuen Punkte berechnet und anschließend mit den übrigen Elementen (z.B. Verbindungslinien) ergänzt.
In meinem Programm kann man den C60 „abfeilend“ vom Würfel erzeugen. Bei SHAPE kann man die Zentralabstände ebenfalls variieren, was aber viel mehr Arbeit macht als einfach mit der rechten Maustaste zu ziehen:



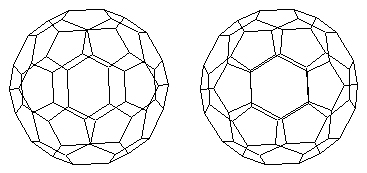






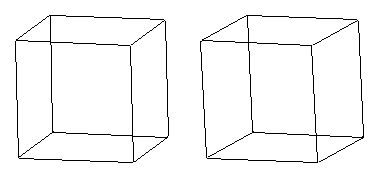



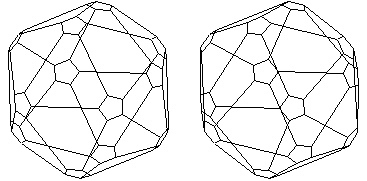

Kommentar abgeben