2.7.2.4 Eutektisches Gefüge als Mischung linearer und flächiger Effekte im Volumen
Eutektikum: Man bezeichnet eine zwei- oder mehrphasige Mischung als eutektisch, wenn für ihre Zusammensetzung ein Minimum des Schmelzpunktes besteht.
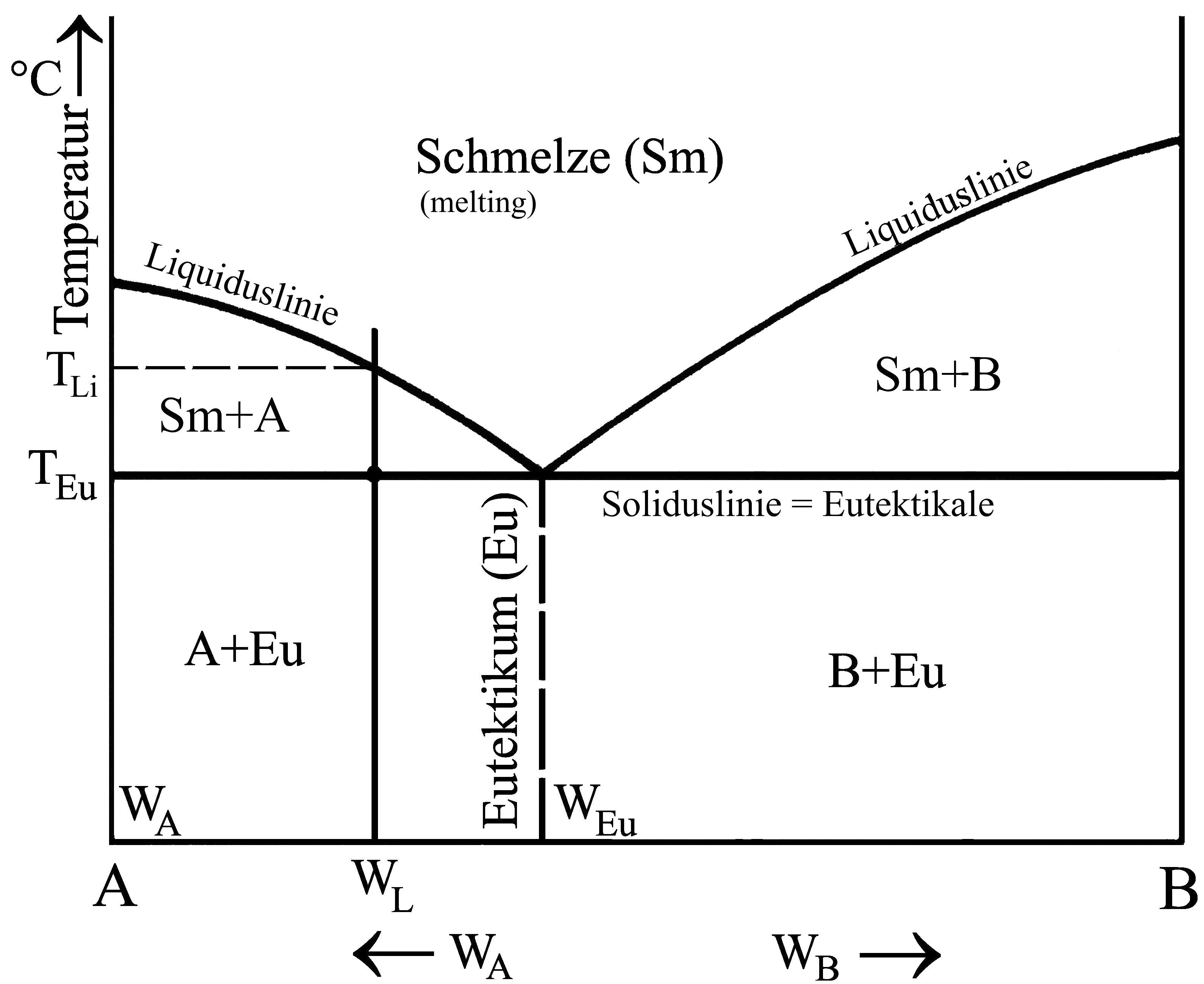
Das Spannende am Eutektikum ist, dass bei einer Ausgangskonzentration der Schmelze, die neben der eutektischen Konzentration liegt, erst eine der beiden Komponenten A oder B kristallisiert (bei komplexeren Zusammenhängen als abgebildet auch als ein entsprechender Mischkristall), wodurch sich die Konzentration der Restschmelze entlang der Liquiduslinie verschiebt, bis bei weiterer Abkühlung (merke: neben der „normalen“ Abfuhr der thermischen Energie muss auch die Kristallisationswärme abgeführt werden!) schließlich der eutektische Punkt erreicht wird, bei dem die Energieabfuhr NUR noch die Kristallisationswärme betrifft. Das ist der Grund, warum man im allgemeinen davon ausgehen kann, dass hier die Kristallisationsgeschwindigkeit (Masse pro Zeit) bei konstanter Kühlleistung ein Maximum erreicht.
Das Besondere an diesem Prozess ist, dass aus einer Phase direkt und rückgekoppelt gleichzeitig zwei neue Phasen entstehen, was die mögliche Geometrie der entstehenden Struktur einschränkt.
Die Techniker (Werkstoffkundler, Metallurgen) und die sammelnden Wissenschaftler (Mineralogen und besonders Petrologen der plutonischen metamorphen Gesteine) haben eine riesige Kenntnis und eine reiche Erfahrung mit den daraus entstehenden Gefügen.
Wir wollen uns aber – wie immer! – dumm stellen und schauen, ob man aus einfachen Überlegungen („first principles“) tragfähige Voraussagen treffen kann.
Also: Normalerweise sollten uns in der Schmelze schwimmende Kristalle/Mischkristalle entweder der reinen/gemischten Phase A oder B vorliegen, wenn wir bei der Abkühlung des Systems den eutektischen Punkt erreichen. Diese Kristalle sind aus sich stochastisch bildenden Keimen entstanden und meist eingermaßen isomorph (wenn sie innen schwimmen) oder stengelig anisotrop (am Gefäßrand und an der Oberfläche). Da die Wärmeabfuhr normalerweise über eine der Grenzflächen des Gefäßes erfolgt, sollte dort der eutektische Punkt zuerst erreicht werden. (Man sieht, schon hier ist es eine Frage der Stärke der Transportprozesse von Wärme und Stoffkomponenten, wo welche Bedingungen herrschen. Man sieht außerdem, dass je nach Transportstärke im festen Zustand eine Zonierung der Kristalle eintreten muss.) Zwischen ihnen ist noch Platz, der von der Restschmelze eingenommen wird.
Bei der Kristallisation der eutektischen Restschmelze müssen die Phasen A und B gleichzeitig im gegebenen Verhältnis abgeschieden werden. Das ist eine neue Sonderbedingung gegenüber dem bisherigen Verlauf der Abkühlung. (Indirekter Beweis: Wäre es nicht so, würde sich die Konzentration der Schmelze verändern, was zwangsläufig zu höherem Schmelzpunkt und also zu sofortigem Abscheiden der überflüssigen Phase führte…) Wozu führt diese Bedingung?
Schärfer gefragt: Wer sortiert die in der Schmelze gemischten Bausteine so, dass zwei Sorten Kristalle gleichzeitig wachsen können? Welche energetischen Prozesse brauchen welche Zeit?
Man merkt, dass sich jetzt zwei Transportprozesse gegenseitig beeinflussen: Wärmetransport und Teilchentransport.
Der Wärmetransport ergibt sich aus den beiden Schmelzwärmen der beiden Phasen (also der inneren Bindungsenergie jeder der festen Phasen im Vergleich zur mittleren der Schmelze) UND der Grenzflächenenergie zwischen beiden Phasen. Die Wärmestromdichte ist von Temperaturgradient und Wärmeleitzahl abhängig.
Die Teilchenstromdichte ist vom Diffusionskoeffizienten und dem Konzentrationsgradienten abhängig.
Gekoppelt sind beide Prozesse über die gemeinsamen Bilanzen (die Energie aus dem Phasenübergang hängt mit dem Volumen der übergegangenen Phase und also mit dem zeitlichen Ergebnis der Diffusion zusammen), das heißt über die Zeit. Das erst macht es spannend. Wir müssen also die beiden oben separat aufgestellten differentiellen Denkansätze (übliche Herangehensweise des Physikers) koppeln und erhalten über die Zeit und die Stromdichten ganz nebenbei die Geometrie und also das „Gefüge“ als Randbedingung.
Die erste Überlegung (eigentlich erst einmal eine Hoffnung) ist, welche Schlüsse man aus einer Bilanzbetrachtung ziehen kann, die zweite Überlegung betrifft dann den Weg, wie diese Bilanz in der Realität erreicht wird. Die erste Überlegung wird zu grundsätzlichen Struktur-Phänomenen führen müssen, die zweite zum Maßstab der Struktur.
Erste Überlegung
Ich frage mich also, was denn energetisch und zeitlich „günstig“ wäre, und komme darauf, dass es kurze Diffusionswege und kleine Grenzflächen (beides relativ zum umgesetzten, also kristallisierten Volumen gesehen) sein müssten.
Nun mache ich mein geliebtes Geometriespiel mit der Zahl der Dimensionen (a sei eine charakteristische Länge vom Mittelpunkt zum Rand):
– nulldimensionale Kristallkeime können durch kleine Würfel beschrieben werden, die aus sechs Teilpyramiden (Spitzen treffen sich im MP) bestehen, wozu ein mittlerer Diffusionsweg von a/4 (Schwerpunkthöhe der Pyramide) und ein Oberflächen-Volumen-Verhältnis von 3/a = 24a²/8a³ gehören: a/4 * 3/a = 3/4
– eindimensionale Kristallkeime können durch quadratische Prismen beschrieben werden, die aus vier Dreieckprismen zusammengesetz gedacht werden können, für die ein mittlerer Diffusionsweg von a/3 (Schwerpunkt des Dreiecks) und ein Oberflächen-Volumen-Verhältnis von 2/a = 8a²/4a³ gehören: a/3 * 2/a = 2/3
– zweidimensionale Kristallkeime können als Platten beschrieben werden, die aus zwei Plattenschichten gedacht werden können, für die ein mittlerer Diffusionsweg von a/2 und ein Oberflächen-Volumen-Verhältnis von 1/a = 2a²/2a³ gehören: a/2 * 1/a = 1/2
Ergebnis:
- Für eine hemmende Dominanz des Diffusionsweges wären isometrische Kriställchen die beste Lösung
- Für eine hemmende Dominanz der Grenzflächenenergie wären dünne Plättchen die beste Lösung
- Für Gleichwertigkeit beider Aspekte wären dünne Plättchen die beste Lösung
Die Stäbchen-Variante kommt also nach der ersten Überlegung gar nicht vor!
(Man könnte sie mit einer passenden Linearkombination von Potenzen statt eines Produkts beider Komponenten natürlich auch nach vorn bringen…)
Zweite Überlegung
Bei einem „klassischen“ Wärme-Abtransport durch Wärmeleitung „nach außen“ (also keine Tricks wie magnetische Effekte usw. usf.) ergibt sich eine geschlossene Eutektikum-Isothermenfläche parallel zur (somit ebenfalls geschlossenen) Phasengrenze (Unterkühlung und Wachstumsgeschwindigkeit darf man in erster Näherung als proprtional ansehen, deshalb lediglich Parallelität und nicht Identität), aber keine Temperatur-Welle in longitudinaler (Außen-) Richtung (mit hypothetischer Vervielfachung der Phasengrenzfläche). (Eine transversale Buchtung der Isotherme kann je nach Schmelzwärme beider Phasen natürlich auftreten.)
Daraus folgt, dass die Diffusionswege in unmittelbarer Nähe der Phasengrenzfläche liegen müssen und also Strukturen bevorzugt sein müssen, die sich senkrecht zur Phasengrenzfläche stetig reproduzieren können. Das sind aber nicht die schachbrettartig gedachten Würfelchen, sondern Stäbchen oder Platten! (Wer sollte den Befehl geben, wann die Diffusionsrichtung für die Würfelchen zu kippen hätte? Das wäre eine oben ausgeschlossene longitudinale Parameter-Welle, oder zeitlich gesehen eine Schwingung.)
Betrachtet man zusätzlich die Zeit in Verbindung mit der Diffusionskonstanten, so ist es natürlich möglich, dass überghaupt keine geordneten Diffusionswege zustande kommen können und sich eine stochastische Mikrostrutur nulldimensionaler Phasengebiete bildet (Basalt).
Im Übergang folgt daraus, dass sich die stabile Größe der Strukturelemente reziprok zur Abkühlgeschwindigkeit verhält. (Dass sich nicht weitere Keime bilden, liegt daran, dass Keimbildung eine größere Unterkühlung erfordert als das in der Geschwindigkeit unterkühlungsproportionale Wachsen vorhandener Strukturen.)
Fazit
- Die Plattenstruktur kommt bei beiden Überlegungen zusammen am besten weg. Sie wird auch sowohl in der Metallurgie (Perlit im Stahl) als auch in der Petrologie (Schriftgranit bei den plutonischen Gesteinen, perthitische Entmischung in den Feldspäten) ausführlich dokumentiert.
- Die laterale Ausdehnung der Platten ist nicht unbegrenzt und beträgt selten deutlich mehr als das Zehnfache ihrer Dicke, „Versetzungen“ sind also normal und weisen auf die gleichen Zusammenhänge zwischen den Dimensionen wie bei den Riffeln und Falten etc hin. Außerdem sind „kurze Platten“ und „geplättete Säulen“ sowohl geometrisch als auch genetisch sehr miteinander verwandt…
- Die Größe der Strukturelemente hängt reziprok mit der Kühlleistung zusammen. Außerdem ist auch die Form der Strukturelemente davon abhängig, weil der mittlere Diffusionsweg in die Betrachtung einfließt.




Kommentar abgeben