Fibunacci-Zahlen und Goldener Schnitt
Gibt es auch bei den natürlichen Zahlen eine Überstruktur, die quasi „selbstorganisiert“ entstehen kann?
Wenn in der Natur etwas „wächst“, so kann es zum Beispiel der stetigen „Wachstumsfunktion“ folgen.
Es kann aber auch aus sich selbst heraus „zellulär“ wachsen.
Oder man macht eine noch einfachere Vereinbarung:
„Jede folgende Zahl soll die Summe der beiden vorangegangenen sein!“
Die beiden Startzahlen legt man willkürlich (zufällig!) fest.
Was macht nun solch ein „Automat“??
Hier das excelperimentelle Ergebnis (kann man auch schnell schriftlich nachrechnen):
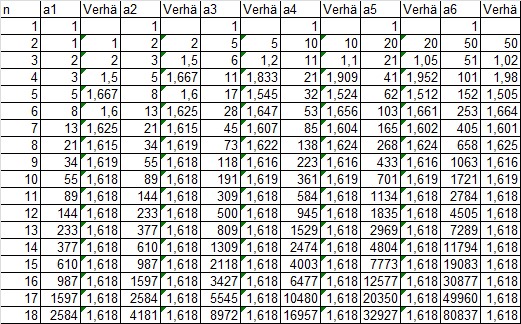
Tabelle der Zahlen-Entwicklung und ihrer nachbarlichen Verhältnise. Die Zahlen der Spalte a1 nennt man („ursprüngliche“) „Fibunacci-Zahlen“.
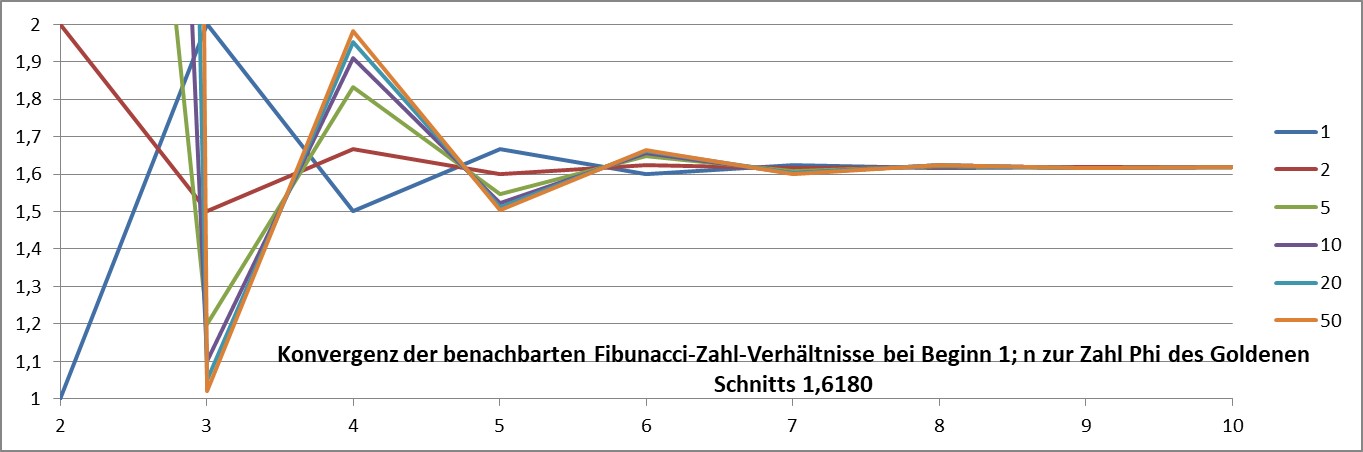
Man erkennt eine schnelle Konvergenz bei völlig verschiedenen Anfangs-Pärchen von Zahlen (1; n).
(Man könnte auch mit höheren Zahlen oder viel kleineren beginnen, die Konvergenz ist davon unbenommen, sogar wenn eine oder beide negativ sind:
Nur zwei Nullen ergeben logischerweise keine vernünftige Folge von Summen…)
In geometrischer Hinsicht ergeben die Fibunacci-Zahlen ein stetig wachsendes zweidimensionales Gebilde, zum Beispiel ein Rechteck aus den Quadraten der Fibunacci-Zaheln:

Man erkennt, dass man das Quadrate-Rechteck (Seitenverhältnis nähert sich fortlaufend dem Goldenen Schnitt an!) leicht mit weiteren (sich automatisch ergebenden) Fibunacci-Zahlen erweitern kann, weil jedesmal eine neue Seitensumme aus den alten gebildet werden muss. Das nächste Quadrat würde also – gegen den Uhrzeigersinn fortgeführt – unten angesetzt werden müssen.
Nimmt man Punkt statt Quadrate und ordnet die im konstanten Winkel an, so ergibt sich folgendes Bild:
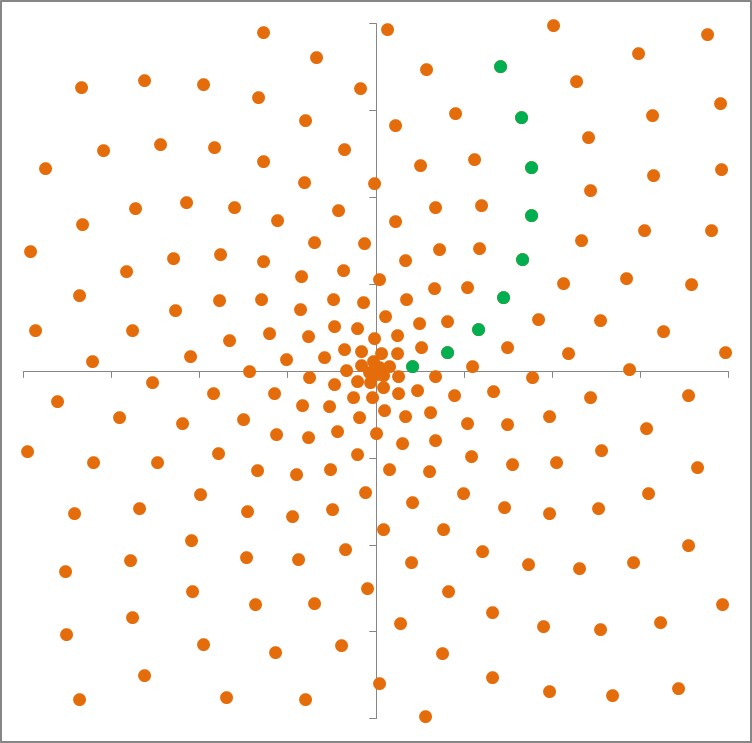
Man findet in diesem Bild einer Spirale mit dem Exponenten 2 auch „Überspiralen“, grün markiert, wenn man nur jeden k-ten Punkt färbt, und wenn k eine Fibunacci-Zahl ist: hier k = 21.
(Ein dem Kaktus besser angepasster Spiralen-Exponent 1,4 ist dort zu sehen!)
Man kann dieses Bild radizieren (die Wurzel aus den Zentralabständen ziehen) und erhält nun folgende Anordnung, die der Sonnenblumen-Kern-Anordnung entspricht :
Übrigens:
Der Nachbar-Verhältnis-Wert, in dem alles konvergiert, egal, womit man die Additions-Zahlenfolge beginnt, ist der „Goldene Schnitt“ 1,618033989.
Dessen Definition ist, dass das
Verhältnis der großen Zahl zur kleinen Zahl gleich dem Verhältnis der Summe beider Zahlen zur großen
sei.
Der „Goldene Schnitt“ wird in der Kunst viel verwendet:
– als Seitenverhältnis eines Rechtecks
– als Abstandsverhältnis zu Fixpunkten oder -kanten
– als Winkelverhältnis usw. usf.
Er kommt in der Natur als Verhältnis in komplexeren Gegenständen wie regelmäßigen Fünfecken, platonischen Pentagon-Dodekaedern oder Sonnenblumen-Kern- oder Kaktus-Stachel-Anordnungen vor. (Dort genauer behandelt.)
Er wird als sehr harmonisch empfunden, weil man wahrscheinlich ein Gespür für eine „innere Ordnung“, zumindest aber ein „inneres Prinzip“ empfindet, das sich selbst treu ist.
Der mathematische Zusammenhang dafür ist
a/b = (a+b)/a
Aufgelöst ergibt das
a = (1+√5)*b/2 = 1,618033989 * b
Beispiel in Zahlen mit a=1 und b = 0,618:
1 + 0,618 = 1,618 und also 1/0,618 = 1,618/1
was auf den ersten Blick kurios erscheint, aber eben die einzige Lösung dieser „seltsamen“ Bedingung ist.
Mit dem Goldenen Schnitt kann man noch viele kurios erscheinende Gleichungen aufstellen, die hier den Rahmen sprengen und also im Selbststudium erarbeitet werden können…