2.4.3.9 Die GROSSEN fressen die kleinen
Kann man verstehen, wieso „gewachsene“ Gebilde wie Tropfen oder Kristalle oft eine nur geringe Variation der Exemplargröße aufweisen? Warum sind oft keine „kleinen Babys“ darunter zu finden, die vielleicht später „auf die Welt“ gekommen sind und noch nicht groß werden konnten?
Nun, bleiben wir uns treu und vereinfachen das Prozess-Problem erst einmal schrittweise und verkomplizieren es dann wieder schrittweise, wobei bei jedem Schritt Klarheit über den vorangegangenen herrschen sollte.
Das Gesamtproblem heißt, dass wir verstehen wollen, warum die Streubreite der Größe der gewachsenen Objekte oft so gering ist.
Erste Frage:
Betrachten wir einen Endzustand oder einen Anfangszustand oder sind wir mitten im Prozess?
Erste Vereinfachung:
Wir betrachten den Prozess. Da haben wir einen Gesamt-Strom an der Grenzfläche von Objekt und Umgebung, der sich aus der Differenz von Hin-Strom und Weg-Strom ergibt. Wenn wir von dem Gedanken ausgehen, dass wir es mit thermodynamischen Zufallsprozessen zu tun haben, so sind für diesen Prozess zwei Größen von Bedeutung:
– energetische Bedingungen der Grenzfläche selbst (Bindungsenergien je Anlagerungs-Punkt [diskrete Betrachtung wie bei Kristallen] oder -Fläche [stetige Betrachtung wie bei flüssigen Keimen im Gas: Krümmung oder Radius])
– Angebote der Umgebung (als „Konzentration“ beschreibbar)
Zweite Frage:
Ist die Umgebung endlich oder unendlich?
Zweite Vereinfachung:
Wir beginnen mit einer unendlichen Umgebung, das heißt, ihre Konzentration ist nicht abhängig von den schon gebildeten Objekten, sie stellt also ein unendliches Reservoir dar.
In diesem Falle können wir auf darauf zurückgreifen, dass sich eine „stabile“ Objekt-Größe berechnen lässt, für die das Strom-Gleichgewicht „Strom gleich Null“ aufstellbar ist.
Für den „natürlichen“ Fall, dass mit steigender Objektgröße (wegen des sinkenden „Innendrucks“ wegen der sinkenden Krümmung der Obefläche bei gegebener Oberflächenspannung) die Gleichgewichts-Konzentration sinkt, wachsen alle Objekte solange, bis sie den gesamten zur Verfügung gestellten Raum einnehmen. Führt man den Begriff „Übersättigung“ ein und meint damit den Konzentrations-Überschuss gegenüber dem Gleichgewicht mit der ebenen Oberfläche (Kugel mit unendlichem Radius…), so kann man einfacher formulieren, dass mit steigender Übersättigung der Keimradius sinkt und für kleine Bereiche eine Linearität zwischen beiden annehmbar ist.
Allerdings ergibt sich aus dieser Betrachtung auch, dass für eine bestimmte Konzentration eine Gleichgewichtsgröße des „Keims“ existiert, der theoretisch weder wächst noch schrumpft. Statistische Prozesse führen aber dazu, dass einige mit gewisser Wahrscheinlichkeit doch wachsen, und zwar beschleunigt, oder schrumpfen, und das auch beschleunigt… Man kann in „nullter“ Näherung dann auch annehmen, dass die Wachstumsgeschwindigkeit proportional der Übersättigung ist und korrigierend in „erster“ Näherung diese proportional zur Differenz der Konzentration zur GG-Konzentration der aktuellen Keimgröße machen. Darus folgt eben, dass die Keime, sobald sie wachsen können, beschleunigt wachsen müssen.
Man sieht schon, dass das in der Realität nicht vorkommt, dass man einen unendlichen Raum beschleunigt vollständig ausfüllt…
Also: Verzicht auf die zweite Vereinfachung!
Damit steht die Aufgabe jetzt:
Wie wachsen Keime in einer endlichen Umgebung?
Neue Vereinfachung:
Wir gehen von einem zweidimensionalen isotropen endlichen Raum aus, in dem sich eine endliche Menge des Stoffes befindet, der aus Keimen isotrope Objekte (also kreisförmige) bilden soll.
Nächste neue Vereinfachung:
Die Diffusionskonstante des Stoffes soll im Raum außerhalb der gebildeten Objekte so groß sein, dass sie nicht verzögernd auf den Wachstumsprozess wirkt.
Dann können wir folgenden Ausgleich im Prozess feststellen:
Je größer die gebildeten Objekte werden, desto mehr verarmt die Umgebung, desto niedriger wird ihre Stoff-Konzentration, desto langsamer wachsen die Objekte. Da aber die für das Wachsen erfordeliche Konzentration ebenfalls objektgrößenabhängig ist, wachsen erstens die Großen schneller als die Kleinen und hören zweitens die Kleinen eher zu wachsen auf als die Großen und fangen sogar an, sich aufzulösen, während die ganz Großen noch weiterwachsen. Am Ende sollte nur ein ganz großes Objekt (Kreis) übrigbleiben, in dem aller Stoff enthalten ist, der dem endlichen Raum entnommen worden ist, bis dessen Konzentration genau der radiusabhängigen Gleichgewichtsbedingung entspricht. (Da wir den Diffusionsprozess als schnell genug eingerichtet haben, „weiß“ also jedes Objekt, welche Gesamtkonzentration überall vorliegt.)
Was passiert beim Verzicht auf die letzte neue Vereinfachung?
Bei einer kleineren Diffusionskonstante kommt die lokale Erniedrigung der Konzentration erst „verspätet“ an anderen Objekten an. Hier empfiehlt sich eine Modellierung, um zu beobachten, ob das unter bestimmten Parameter-Umständen zu Oszillationen der Objektgröße führen kann. Aber auch hier wird die Tendenz sein, dass sich zufällig größere Objekte auf Kosten der Kleinen weiter vergößern.
Offen gebliebene Frage:
Woher kommen die typischen Gesteins-Strukturen (z.B. Granit oder Porphyr) mit etwa gleichgroßen Objekten einer bestimmten Phase, eingebettet in andere?
Offenbar hat der Transport (Diffusion) aufgehört, weil sich eine weitere Prozessgröße (z.B. Temperatur) so verändert hat, dass unsere anfangs vermuteten Bedingungen nicht mehr gelten.
Also versuchen wir es wirklich am Anfang mit einer 2-D-Modellierung, bei der in einem endlichen Raum eine endliche Anzahl von Start-Objekten statistisch schwankender Größe statistisch verteilt wird, wobei eine Anfangs-Konzentration des Rest-Raums vorgegeben werden kann. Im Zeitablauf soll dann der Prozess beobachtet werden. Eine weitere Einflussgröße kann dann hinzugenommen werden und ein Vergleich zwischen 2D- und 3D-Modellierung angestrebt werden.
A) Modellierung der Veränderung von stetigen 2-D-Objekten
Was passiert am 2-D-Objekt, wenn Teilchen angelagert oder abgegeben werden? Es verändern sich die Oberfläche (hier die Umfanglänge) und das Volumen (hier der Flächeninhalt)! Wir haben es also mit der Überlagerung von Zusammenhängen unterschiedlicher Dimension zu tun, was genau dem Anliegen dieser Abschnitte entspricht, und zwar wollen wir es hier erst einmal stetig probieren, also mit phänomenologischen Gesamtgrößen wie spezifischer Volumenenergie (hier: spezifische Flächenenrgie wf in J/m²) und spezifischer Oberflächenenergie (hier spezifischer Randlängenenergie wr in J/m) arbeiten.
Wir können folgende Zusammenhänge formulieren:
Die Gesamt-Flächenenergie ist spezifische Flächenenergie mal Fläche
Wf = wf*A
Die Gesamt-Randlängen-Energie ist spezifische Randlängenenergie mal Randlänge
Wr = wr*L
Setzen wir für A und L Kreise mit dem Radius r an, ergeben sich:
Wf = wf*pi/4*r²
Wr = wr*2pi*r
Was passiert, wenn sich die Größe des Kreises durch Materie-Aufnahme psoitiv verändert, der Kreis also größer wird?
Dann erhöht sich die Flächenenergie (Bindungsenergie wird frei) und es erhöht sich die Randlängenenergie (ein anderer Betrag an Bindungsenergie wird frei), wodurch sich sowohl die Energie als auch die Energiedichte des Objekts ändern.
Zählt man die Randelemente sowohl zur Fläche als auch zum Rand, muss man die Randenergie negativ ansetzen und erhält für die Gesamtenergie des Wachstums-Prozesses W zwei konkurrierende Teil-Prozesse:
W = Wf-Wr =pi*(wf/4*r²-2*wr*r)
Setzen wir für W=0 den „kritischen Keim“ mit dem Radius r*, der sich gerade nicht auflöst oder wächst, so erhält man
r* = 8 wr/wf
Das ist ein hübsches Ergebnis, aber völlig unbefriediegend, weil das Angebot an Wachstumsmaterie (z.B. über eine Konzentration beim Wachstum aus der Lösung oder über eine Temperatur beim Wachstum aus der Schmelze) überhaupt nicht vorkommt und somit auch keine zeitliche Modellierung eines Prozesses möglich ist.
Wir brauchen also noch eine Größe, die mit einer Prozessgeschwindigkeit zu tun hat. Diese könnte also die „Übersättigung“ der Lösung oder „Unterkühlung“ der Schmelze sein. Wir ahnen schon, dass das nicht trivial ist, weil genau der kritische Keimradius ebenfalls von diesen abhängig sein muss. Es ist deshalb qualitativ nicht falsch, diese Abhängigkeit für die Modellierung in die spezifischen Größen hineinzunehmen, die damit allerdings ihre Eigenschaft als globale Konstanten verlieren. Der Vorteil ist, dass wir eine (gewünschte!!) Rückkopplung in den Prozess bekommen.
Eine erste Berechnung mit Differenzengleichungen in EXCEL zeigt wirklich die erwarteten Ergebnisse der Wirkungskette
– größenabhängige individuelle Übersättigung lässt Keime individuell unterschiedlich schnell wachsen
– alle Übersättigungen reduzieren sich
– für die Kleinen entsteht zuerst eine Untersättigung, so dass sich diese auflösen
Für nur zwei Keime im Radius-Verhältnis 2:1 ergibt das folgenden Funktionsgraphen r(t):

Ein Spielchen in EXCEL ohne VBA erlaubt auch mit erträglichem Aufwand die Darstellung von drei verschiedenen Keimen:

Der Kleinste ist jetzt schneller aufgefressen und der GROSSE kann noch fetter werden… Dem Mittleren ging es eine Weile gut, aber dann…
Der GROSSE wächst übrigens nach dem Verschwinden der Kleinen noch ein klein wenig weiter, was aber im Diagramm nicht zu erkennen ist. Das Gleichgewicht ist relativ schnell – je nach Einstellung der entsprechenden Konstante für die Wachstumsgeschwindigkeit, vergleiche den Anfangsanstieg als Maß für die Ausgleichszeit – erreicht.
Legt man die Keime in ihrer Größe dichter beieinander an (<10%), so differenziert es sich anfangs eben langsamer:

Da die Radien eigentlich wenig anschaulich sind, im 2D aber die Flächen für die im Phasen-Übergang umgesetzten Mengen, so hier noch das Diagramm der Entwicklung der drei Kreis-Flächen, die in summa nach dem anfänglichen schnellen Wachstum etwa konstant bleibt:
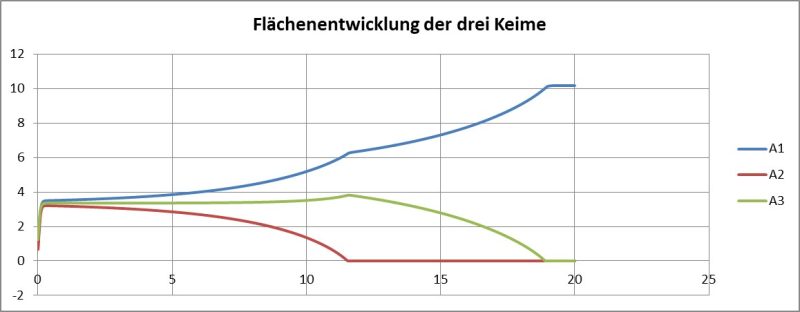
Die abgeschiedene „feste“ Fläche wächst aus der 2D-„Lösung“ hier von 2,2% auf 10,2% der Gesamtfläche an. Die Konzentration der Restlösung ist erst dann konstant, wenn nur noch ein Kreis übrig ist.
Man erkennt deutlich, dass sich zwei Prozess-Typen ablösen:
Zuerst findet eine negative Rückkopplung statt, es läuft also ein Ausgleichsprozess: Je mehr Fläche gewachsen ist, dest mehr verarmt die Rest-Lösung.
Dann kommt es zu einer positiven Rückkopplung, es läuft ein Wachstumsprozess: Je kleiner die Kleinen werden, desto schneller lösen sie sich auf und lassen die Großen wachsen, wobei die Restlösung nur unwesentlich ihre Konzentration ändert.
Der erste Prozess läuft wesentlich schneller ab (wir haben eine sehr große Diffusionskonstante gewählt!), weshalb man das Diagramm stark strecken muss, um die Ausgleichskurve genießen zu können:

Dabei sind viele Parameter in das EXCEL-Modell frei eingebbar: Start-Konzentration der Lösung, GG-Konzentration (coo) der ebenen Grenzfläche (hier im 2D also eine Gerade mit dem Radius oo), Konzentration in der festen Phase (z.B. 100%), Exponent (r-exp) und Faktor (f) der Anhängigkeit der GG-Konzentration vom Radius
| co(r) = coo*(1+f/r^(r-exp)) |
sowie alle Start-Radien der Keime. Die Wachstumsgeschwindigkeit wird nun als proportional zur radiusabhängigen Übersättigung (Differenz der aktuellen Lösungskonzentration cl und der radiusabhängigen GG-Konzentration co(r)) angesetzt (Faktor 1, da Streckung oder Stauchung der Darstellung des Prozesses mit dt erfolgen kann):
| dr = (cl – co(r))*dt |
(Es sind hier also noch keine Diffusionshöfe um die Keime berücksichtigt. Im diffusionsabhängigen Modell müsste dann für eine Diffusionskonstante gegen Unendlich das gleiche Ergebnis herauskommen!)
Für eine statistische Verteilung statistischer Keim-Größen in der Fläche ergibt das eine Entwicklung im VB-Modell, die der nun geübten Erwartungshaltung entspricht (schnelles Wachstum aller Keime beim Abbau der Anfangs-Übersättigung, langsamer Umbau der Größen), hier für 36 Keime :
In dem Moment, wo nur der Größte übrig bleibt, gibt es noch eine geringe Übersättigung vom Abbau der letzten Kleinen, die dann zum geringen Reifewachstum des Größten beiträgt. Unabhängig von der Zahl der Anfangskeime hat der Größte eine Abmessung, die – bei gegebenem Volumen – nur von der Gesamtmenge des gelösten Stoffes und der GG-Konzentration der ebenen Grenzfläche abhängt. (Die Zahlenwerte sind links in den Labels abzulesen. Die Differenzengleichungen sind so parametrisiert, dass hier über 8000 Rechenschritte absolviert worden sind (etwa zehn Minuten auf meinem alten LapTop…).
Für 121 Keime sieht es nicht wesentlich anders aus (die Wahrscheinlichkeit sehr ähnlicher Keimgrößen wächst allerdings, was das Tempo des Prozesses verringert):
Übrigens funktioniert das Ganze auch rückwärts, will sagen, beim Eintrag der Keime von außen, wenn die Lösung sehr untersättigt oder das Lösungsmittel sogar rein ist: Dann lösen sich so lange Kristalle auf (es wächst also anfangs keiner!), bis wieder der Größen-Umbau zu Lasten der Kleinen stattfindet (sofern überhaup genügend Material da ist, um eine Übersättigung zu erzeugen):
Nun gilt es also, die Rückkopplung über die Diffusionshöfe mit zu berücksichtigen. Sie werden den Prozess in der ersten Erweiterung stark verlangsamen und in der zweiten die Radialsymmetrie trotz isotroper Materialeigenschaften zurstören!
Wir gehen in erster Näherung davon aus, dass radialsymmetrische Diffusionshöfe entstehen, die wir später übelagern werden. Die Stromdichte ist proportional dem Konzentrationsgradienten. Ein hoher Strombedarf erfordert also einen hohen Gradienten. Im stationären zweidimensionalen Fall ist der Gradient proportional zu 1/r (im dreidimensionalen zu 1/r²). Das liegt daran, dass die Stromdichte mit der Oberfläche (hier eindimensionaler Umfang) multipliziert im stationären Fall radiusunabhängig sein muss. Das bedeutet, dass das Integral über den Gradienten, also die Konzentration, einen logarithmischen Verlauf hat. Das klingt für die Konstruktion eines Anfangszustandes etwas abenteuerlich! Das heißt im Umkehrschluss, dass wir grundsätzlich keinen stationären Zustand erwarten dürfen, wenn wir nicht Material nachliefern (was wir ja auschließen), also eine Randkonzentration aufrechterhalten. Wir haben es nun also mit zwei Arten von Differenzengleichungen zu tun: verknüpften zeitlichen und räumlichen! (Diffusionsgleichung: die zeitliche Ableitung der Konzentration ist proportional der zweiten räumlichen Ableitung derselben Konzentration, und außerdem ist die Stromdichte gleichzeitig proportional der ersten räumlichen Ableitung)
Interessant ist, dass wir von vornherein zwei sich überlagernde Tendenzen erwarten dürfen:
– durch den Materialbedarf des wachsenden Keims wird der Umgebung Material entzogen, sie verarmt, wodurch die Übersättigung sinkt und sich im Schnittbild eine „Konzetrationsmulde“ ausbildet, was die Wachstumsgeschwindigkeit erniedrigt
– durch den Radiuszuwachs des wachsenden Keims gerät dieser einerseits in Gebiete höherer Konzentration, was die Wachstumsgeschwindigkeit eröhen sollte, andererseits aber in Gebiete geringeren Gradientens, was den Materialnachschub verringert: beides wirkt auf die Muldenform
Die numerische Integration dieses Prozesses wird also spannend; erst recht ihre Überlagerung bei vielen Keimen.
Wir gehen vom simpel erscheinenden eindimensionalen Fall schrittweise zum dreidimensionalen vor und beginnen mit einem einzigen Keim:
Eindimensional, Einzelkeim, endliches übersättigtes Reservoir
Schon bald merken wir, dass wir an der Grenzfläche ein Problem haben, wenn wir einen allgemeinen Algorithmus für alle diskretisierten ebenen dünnen Schichten anstreben: Die Grenzfläche ist im diskretisierten Fall selbst eine Schicht, deren Konzentration wächst, bis sie die Konzentration des Festkörpers erreicht hat. Dann gehört sie selbst zum Festkörper und gibt die Wachstumseigenschaft an die nächste diskrete Schicht ab. Wollen wir das allgemein formulieren, machen wir am besten eine Zweiteilung: Stromdichte-Berechnung an den Schicht-Grenzen und Konzentrationsänderung aus der Strombilanz zu beiden Nachbarn, was natürlich schichtvolumenabhängig sein muss und damit dimensionszahlabhängig ist.
Damit wir uns nicht in Fehlerbetrachtungen der Numerik verlieren, kann man probieren, ob man eine „Rückgabe“ eventuell überschüssigen Materials des vergangenen Zeittakts aus dem neu definierten „festen“ Element an das nun neu „wachsende“ vereinbart.
Für ein Element („ebene dünne Schicht“) mitten in der Lösung gilt, dass die Konzentrationsänderung proportional der Differenz von Zustrom und Abstrom ist. Beide Ströme sind jeweils proportional der Konzentrationsdifferenz zwischen den benachbarten Schichten, führen aber durch dimensionszahlabhängige Volumenunterschiede zwischen den Schichten zu unterschidlichen Konzentrationsänderungen in diesen.
Für das Element am Rande des Reservoirs gibt es nue einen einzigen Strom, den Abstrom.
Für das „wachsende“ Grenzflächenelement gelten zwei unterschiedliche Prozess-Konstanten (Diffusionskonstante nach außen wie für die anderen auch und Anlagerungskonstante nach innen, in welcher eine Abhängigkeit von der gewählten Schichtdicke stecken muss) und eine getrennte (radiusabhängige!) Gleichgewichtskonzentration (vgl. „Keim“), wodurch ja seine „Senken“-Eigenschaft überhaupt erst hervorgerufen wird.
Es wäre sehr lehrreich, wenn diese Konstanten im Modell veränderbar wären, um ihren Einfluss auf die Ausbildung des Diffusionsprofils in der Lösung studieren zu können (wir wollen hier idealisiert Konvektion jeder Art ausschließen).
Mit 10 Schichten (Konzentration fest: 10, flüssig zum Start: 5, GG: 1) ergibt sich folgendes sehr grobe Bild für exponentiell gestaffelte Prozess-Zeiten von 0 (Start) bis 1000 (Beobachtungs-Ende):

Was kann man sehen?
- Die Phasengrenze wandert von links nach rechts (von Schicht 2 zu Schicht 5) in die Lösung hinein.
- Die Lösung verarmt und bildet einen schwachen Konzentrations-„Trichter“ aus.
- Die Grenzschicht wird jeweils angereichert, bis sie die Konzetration der festen Phase erreicht hat.
- Der Prozess ist abgeschlossen, wenn in der Lösung die GG-Konzentration erreicht ist (hier verdeckt im Diagramm die 1000-er Kurve die 350-er; die letzte diskrete Grenzschicht ist unvollständig gefüllt, in der echten Natur eines Kristalls also noch unvollständig und rauh, was sich aber im mehrdimensionalen Fall durch Oberflächendiffusion incl. Kanten und Ecken noch umgruppieren würde… (vgl. auch die erarbeiteten Zellulär-Modell-Bilder in 1.2.4))
Verringert man die Diffusionskonstante in der Lösung, so stellen sich die Trichter – wie erwartet – naturgemäß tiefer ein (erst ein größerer Gradient liefert den von der Grenzfläche „geforderten“ Strom):

Mit 85 statt 10 Schichten ist der Verlauf schon „glatter“ darzustellen, wieder die Konzentration zu verschiednen exponentiellen Zeiten über der Schicht-Nr. aufgetragen:

Verringert man die Anfangskonzentration der Lösung, so wächst der Keim weniger weit:

Verlängert man den Prozessnoch etwas, wächst der Keim nur noch langsam weiter, bis er quasi fertig ist (Konzentration in der Restlösung entspricht der GG-Konzentration des Keimes, die sich im ebenen Fall nicht ändert):

Man erkennt in den Diagrammen (wenn man die unterschiedlichen Mess-Zeit-Abstände berücksichtigt) sehr gut, wie die zeitliche Änderung der Konzentration an einem festen Ort von der zweiten Orts-Ableitung (Krümmung) abhängt. (Darin steckt die einfache Tatsache, dass bei gleichem Zu- wie Abstrom die Konzentration am festen Ort (hier: Schicht) konstant wäre…) Eine Gerade als Konzentrationsverlauf entsteht also erst nach dem Ende des Keimwachstums. Die Zeitspanne zum Auffüllen einer neuen Schicht wächst deutlich an, weil sich das Reservoir leert (und weil somit der Konzentrationsgradient geringer wird). In dem Moment, wo der „Trichter“ den Rand erreicht, sinkt auch dort die Konzentration des endlichen (!) Reservoirs ab. Nach 10000 Takten ist im unteren Diagramm zu sehen, dass der Prozess im Rahmen der Genauigkeit so gut wie abgeschlossen ist (Ausgleichsprozesse sind mathematisch NIE beendet…).
Radialsymmetrisch zweidimensional, Einzelkeim, endliches übersättigtes Reservoir
Spannend wird nun, ob sich die Radiusabhängigkeit der GG-Konzentration des Keimes und die Volumenänderung der Schichten in Abhängigkeit vom Mittelpunktabstand deutlich sichtbar auswirkt.

Radialsymmetrisch dreidimensional, Einzelkeim, endliches übersättigtes Reservoir

Man kann tatsächlich klar erkennen, dass die Diffusionstrichter steiler (oder besser: stärker gekrümmt) werden, weil für den gleichen Gesamtstrom nach innen immer weniger Fläche zur Verfügung steht, was durch einen grüßeren Gradianeten „ausgeglichen“ werden muss. Gleichzeitig wächst der Materialbedarf nach außen pro Schicht.
Masse-Erhaltungs-Probe für die maximale Keimgröße:
2D:
50%*V != 100%*Vk + 10%*(V-Vk) Vk etwa (126/166)² * V = 0,58V
0,50V != 0,58V + 0,04V = 0,62V
3D:
50%*V != 100%*Vk + 10%(V-Vk) Vk etwa (138/166)³ * V = 0,57V
0,50V != 0,57V + 0,04V = 0,61V
Dieser Fehler ist zu groß, um ihn allein auf die Numerik zu schieben. Also genauer prüfen, ob sich da ein Denkfehler in den Algorithmus eingeschlichen hat! (Rechteck- statt Trapez-Integration?) Interessant ist aber, dass der Fehler dimensionsunabhängig ist…
Ja, es ist ein systematischer Integrations-Fehler des „Rechteck-Typs“. Erledigt.
Nun ist noch zu prüfen, welchen Einfluss die Kombination von radiusabhängiger GG-Konzentration und Diffusionskoeffizient hat. Bei „schneller“ Diffusion nsollte die Konzentrations-Profilform nicht von der Größe „r2“ (Radius der doppelten GG-Konzentration i.Vgl. zur Ebene) abhängen.
Probieren wir das für verschiedene r2:
Das Ergebnis zeigt tatsächlich eine sehr schwache Abhängigkeit bei einem Einzelkeim. Das bedeutet, dass wir bei der Betrachtung der Überlagerung von Diffusionshöfen ledigleich für die Übergangszeit Einflüsse zu erwarten haben, nicht aber für das Endergebnis.
Da die Konzentration der Lösung durch das Wachsen der Keime sinkt, wird die Neubildung von Keimen immer unwahrscheinlicher und trägt zur Verstärkung der Tendenz bei, keine kleinen Objekte finden zu können. Da gleichzeitig der Austausch zwischen den Großen immer langsamer wird, ist es also nicht verwunderlich, in Gesteinen ziemlich gleich große Kristalle des gleichen Minerals anzutreffen.



































Kommentar abgeben