Modellierung
Viele Fragen zur Struktur und ihrer Entstehung sollen auf diesen Seiten mit der Methode der Modellierung untersucht werden. Was bedeutet das?
- Man legt eine Startsituation fest.
- Man legt Regeln fest, mit denen die Basiselemente („Keime“) der späteren Struktur interagieren sollen.
- Man überträgt beides in eine Programmiersprache.
- Man überlässt das System sich selbst und beobachtet, ob es erstens überhaupt eine „Struktur“ ausbildet und ob zweitens diese Struktur „stabil“ ist.
- Man vergleicht das Ergebnis mit der Natur und zieht daraus die Erkenntnis, ob man die Natur verstanden hat oder eben nicht (und feilt unter Umständen an den Basiselementen und Regeln schrittweise so lange herum, bis es besser wird – das macht den meisten Spaß und bringt den meisten Erkenntnisgewinn!).
Wenn man für die Programmierung noch nicht fit ist, macht man das Ganze als „Gedankenexperiment“ oder stark abgerüstet mit Bleistift und Papier (grafisch oder rechnerisch).
(Es empfiehlt sich generell, vor der Programmierung einmal die Regeln für die Basiselemente mit Bleistift und Papier durchzuspielen, um grobe Denkfehler schon vor dem oft nicht unerheblichen Programmieraufwand auszuschließen…)
Hier muss man sehr, sehr deutlich eine scharfe Unterscheidung machen:
MODELLIERUNG <-> SIMULATION <-> ANIMATION/VISUALISIERUNG
Bei einer Visualisierung werden rein geometrische Algorithmen verwendet, um bestimmte Bilder zu erzeugen. Sind sie bewegt, nennt man sie Animation.
Bei einer Simulation wird ein bestimmtes „Bild“ eines physikalischen Zustands erzeugt, indem man anstelle des „Originalvorgangs“ einen Stellvertreter-Algorithmus verwendet, der, so die Hypothese, ebenfalls zu diesem Bild führen muss. Das ist nicht abwertend gemeint, wenn man zum Beispiel einen Wärmetransport mit einem elektrischen Netzwerk simuliert, weil man vermutet, dass die mathematische Form des Prozesses vergleichbar ist. Am Ergebnis erkennt man dann, ob man mit den Erkenntnissen, auf denen die Simulation beruht, auch den simulierten Vorgang selbst beschreiben kann, inwieweit die Übertragung also tragfähig ist.
Bei der Modellierung verfährt man wie oben (von 1. bis 5.) beschrieben. Im Detail heißt das, dass man sich schrittweise an die Realität heranpirscht, indem man die dem Algorithmus zugrundegelegten Naturgesetze so lange verfeinert, bis das Ergebnis der Realität entspricht: Wenn aus den gegebenen Anfangsbedingungen unter den gegebenen Randbedingungen durch Integration über die Zeit (an allen Orten!) ein Prozessergebnis entsteht, das der Realität entspricht, können die verwendeten Gestzmäßigkeiten richtig sein. (Erst eine gut durchdachte Probe bestätigt dann die Hypothese der Richtigkeit!) Kommt etwas anderes heraus, kann das an den Anfangsbedingungen, den Randbedingungen, den Gesetzen oder dem Algorithmus liegen. Es ist also ein weites Feld, das somit Erfahrung voraussetzt und aber auch ermöglicht (auf dem Umweg über den Fleiß und die Beharrlichkeit…).
Insbesondere jener Fall, dass eine schrittweise Verfeinerung der Modellierung schon früher Erfolg hat als erwartet, bringt oft fundamentale Erkenntnisse über komplexe Zusammenhänge (in vielparametrigen Systemen), indem er zeigt, dass bestimmte Aspekte in einem gewissen Rahmen der Parameter vernachlässigber sind. (Das sind sehr hilfreiche Hinweise der Theoretiker für die Experimentatoren zur Optimierung ihrer Arbeit!)
Aber auch auf dem umgekehrten Weg, nämlich dem des Spiels, kann etwas erkannt werden:
Künstlerisch-spielerische Gestaltungslust kann zu „Entdeckungen“ oder zu Erkenntnissen über reale Vorgänge führen, wie mit animierter Computer-Grafik zum Beispiel.
Hier zwei ausgewählte Zitate fremder Gedanken, die nur scheinbar Modellierungen zur Folge haben:
1. Nimmt man einen beliebigen zweidimensionalen Umriss („Hohlform“) und füllt ihn schrittweise mit farbigen Streifen mit jeweils (über den gesamten Umfang!) konstanter Breite, so glaubt man, Achat-Geoden vor sich zu haben. Ergänzt man dieses Spiel noch mit vor der Wachstumsfront zufällig auftauchenden Keimen, bekommt man durch die vermeintlichen „Sphärolithe“ sogar die Illusion eines zweidimensionalen Schnitts durch einen dreidimensionalen Achat hin (was natürlich irreführend ist, weil ein wirklicher Schnitt durch einen wirklichen Achat nicht jede Schicht überall unter gleichem Winkel schneidet, weshalb das Schnittbild einer bestimmten Schicht selbst dann, wenn diese eine konstante Dicke hat, keine konstante Breite aufweisen kann).

Beispiel einer 2-D-Simulation einer Achat-Puzzle-Variante auf der Seite https://n-e-r-v-o-u-s.com der US-amerikanischen Firma Nervous System, Inc.
Es wäre interessant, mit welchen Ansätzen für schwankende Schichtbreiten man die „Echtheit“ erhöhen könnte. Aber: Trotz der Unvollkommenheit des Visualisierungs-Programms für konstante Schichtdicken liefert es einen Hinweis darauf, dass bei echten Achaten
– entweder ein schneller transversaler (lateraler, senkrecht zur Wachstumsrichtung zeigender) Grenzflächen-Effekt die Ungleichmäßigkeit des longitudinalen (parallel zur Wachstumsrichtung) Transports ausgleicht oder auch ein Precursor die Mini-Schichtdicke pro Mini-Wachstumsphase begrenzt
– oder aber zwei sich weiträumig (bzgl. der Parameter) aufhebende Zusammenhänge den Mechanismus des Wachstums bestimmen, wie es zum Beispiel durch Diffusion von/nach außen (wachsende Diffusionslänge) und Wachstum nach innen (sinkendes Restvolumen bei relativ steigender Grenzfläche) der Fall wäre
2. Man lässt um jeden der zufällig verteilten Punkte auf der Ebene die Bereiche hervorheben, in denen dieser Punkt der nächste von allen ist. Die entstandenen Zellen (durch die Mittelsenkrechten der Verbindungsgeraden der Punktpaare reräsentiert) ähneln entfernt den Rissmustern, die einer Energie-Minimierung folgen:
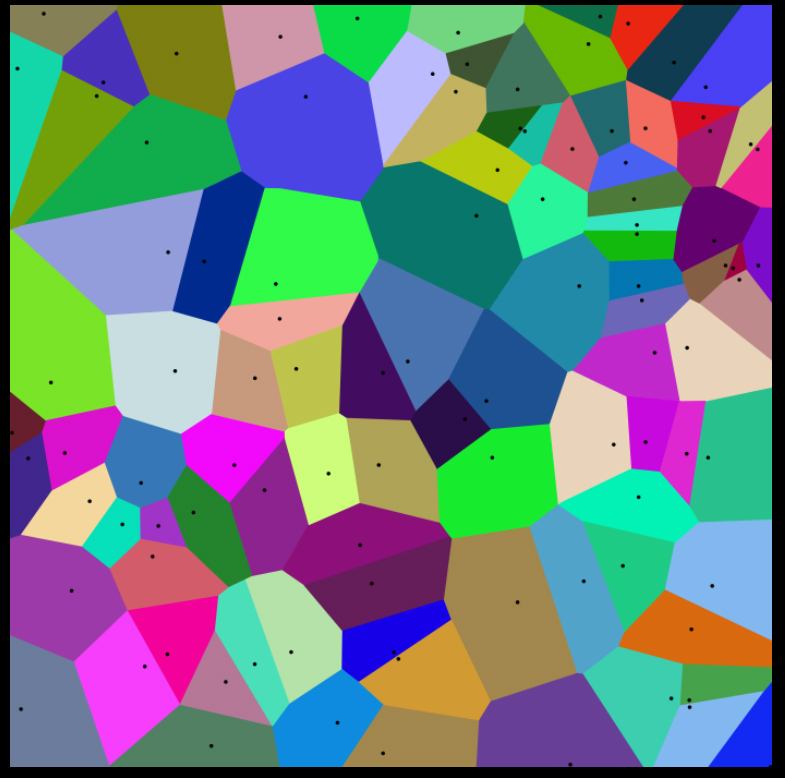
Voronoi-Diagramm, auch Thiessen-Polygone oder Dirichlet-Zerlegung (nach https://de.wikipedia.org/wiki/Voronoi-Diagramm)
Durch Beeinflussung der Statistik könnte man die Ähnlichkeit auch hier erhöhen, wird aber dem echten Ergebnis einer energetisch bestimmten Dynamik in die dritte Dimension (Basalt-Säulen statt Trocknungs-Risse in dünner Schlammschicht) nicht beliebig nahe kommen können.
Hier nun ein relativ einfaches Beispiel einer schrittweisen Annäherung an die Realität durch eine schrittweise Verfeinerung eines Modells (unter bestmöglicher Vermeidung visueller Trugschlüsse):
Modellierung der Hinterrad-Fontäne eines schutzblechlosen Fahrrads
Jeder, der so gern im Regen radelt wie ich, ist schon einmal in der Fontäne seines Vordermanns geradelt, denn anders kann man seinen Windschatten nicht nutzen. Schaut man in diese Fontäne direkt hinein, sieht man fast nichts. Betrachtet man sie leicht von der Seite, sieht man eine interessante Projektion:
Ganz unten am Rad scheint sich ein dünner Film zwischen Rad und Straße zu spannen, darüber fliegen viele Tropfen, darüber wiederum scheint am oberen Rand fast so etwas wie ein kompakter Strahl zu existieren, und ganz oben fliegen wieder ein paar Tropfen für sich.
Warum ist da mittendrin ein Strahl? Gibt es einfache Annahmen, die das „vernünftig“ (also in Übereinstimmung mit einfachen vernünftigen Ansätzen) erscheinen lassen?
Man ist geneigt zu glauben, dass da beim Ablösen des Reifens von der nassen Straße ein Punkt existiert, an dem die Beschleunigung besonders groß ist, weshalb gerade dort die Tropfen davon fliegen und einen Strahl bilden. Schließlich ruht der Reifen ja ganz kurz auf der Straße und bewegt sich dann – exakt mit der Fahrgeschwindigkeit – nach oben, wenn er auf Nabenhöhe ist. Dazwischen muss es ja eine Beschleunigung gegeben haben, oder?? Völlig klar.

Stroboskopische „Normal“-Zykloide als „wahre“ Trajektorie eines Umfangspunktes eines rutschfrei rollenden Rades mit dem Radius 0,5
Diese Beschleunigung ist aber bei genauer Betrachtung die Radialbeschleunigung und zeigt immer in eine Richtung parallel zum Radius (Vorzeichen zu vereinbaren). Erst die gefühlte Überlagerung mit der Translation des gesamten Fahrrads führt also zu dieser falschen Annahme einer nicht konstanten Beschleunigung. Im (unbeschleunigt!) mitbewegten Bezugssystem ist die Konstanz der Beschleunigung eines Umfangspunktes sofort einsichtig, denn dort dreht sich das Rad einfach „auf der Stelle“.
Gedanken-Experiment:
Ein nasses Rad dreht sich, in der hier vertikalen Achse gelagert, und schleudert Tropfen in alle Richtungen gleich schnell, wobei sie nach unten beschleunigt (Schwerkraft) und gegen die Bewegungsrichtung gebremst (Luftreibung) werden. (Siehe Wasserrakete als Beispiel 2 im Abschnitt Numerische Integration!) Kippt man das Rad nach oben (Achse waagerecht, Drehrichtung nach links), so ergibt sich ohne Berücksichtigung des Wasserverlustes durch die abspritzenden Tropfen eine Serie von Schwerkraft-Parabeln. (Hier ist die Schwerkraft NUR für die Flugbahn, nicht aber für die Ablösung vom Reifen verantwortlich!)
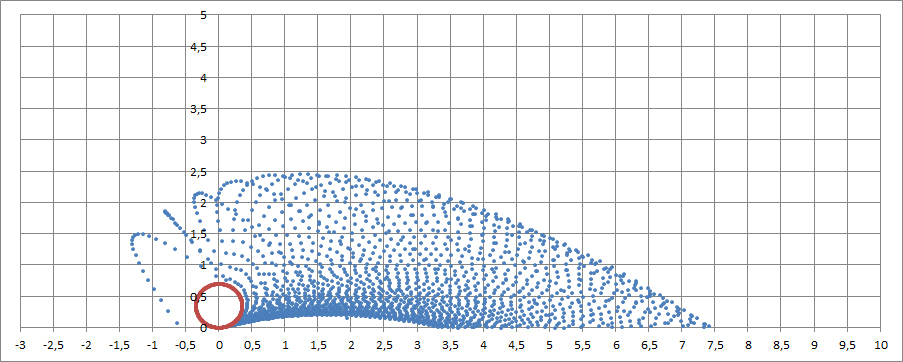
Man erhält (das geht alles noch spielend leicht mit den analytischen Lösungen der Überlagerung von freiem Fall und gleichförmig geradliniger Bewegung sowie Ausgleichsprozess der Luftreibung!) das folgende Bild, wenn man schrittweise einen Wind von links (im ersten Bild ohne Wind, im zweiten Bild mit Wind in Größe der Umfangsgeschwindigkeit des Rades, also normaler Fahrtwind, im dritten Bild starker Gegenwind!) hinzufügt, wodurch die Bewegungen des gesamten Rades und der Luft substituiert werden und zu folgenden Tropfen-Flugbahnen führen:
Fügt man nun noch hinzu, dass das Wasser am Reifen ja immer weniger wird, wenn etwas wegspritzt (kann man analytisch durch e-Funktionen oder numerisch integriert machen), so verändert sich das Bild wiederum (Zahlenangaben im Diagramm: Länge/Höhe in Metern):
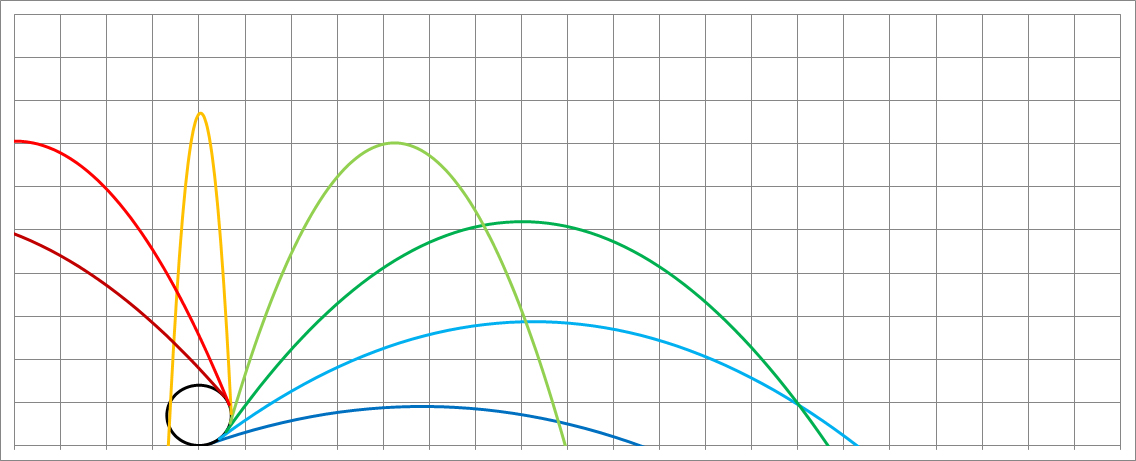
Man sieht tatsächlich einen dichten „Film“ ganz unten und eine leichte Komprimierung ganz oben, an der „Einhüllenden“. Es „stört“ aber ein Artefakt die Betrachtung der Tropfenbilder, der durch den konstanten Zeittakt entsteht und eine Interferenz erzeugt, die nach links gebogene Kurven von unten her erscheinen lässt. Überlagert man den Zeittakt etwas mit einem Zufallswert (nun empfiehlt sich tatsächlich eine numerische Integration zum Beispiel in EXCEL-VBA mit Ausgabe in zwei Spalten für Länge x und Höhe z, welche wegen der Punkt-Darstellung eine einzige Datenreihe bilden dürfen), kann man das fast vermeiden (den Artefakt nicht mit den echten – außer der linkesten sonst nach rechts drehenden – Flugbahnen verwechseln!):
Hier ist jetzt etwa ein Drittel des Radumfangs mit 50 Abreißpunkten belegt, deren Abstand sich mit dem Winkel zum Bodenpunkt leicht vergrößert und deren Zeittakt sich leicht verlängert, um die verringerte Dichte der „Tropfen“ erzeugen zu können (Ausgleichsprozess im Abschnitt „Dämpfung“ – Beispiel 3 – nachlesen!).
Die leichte Überlagerung an der Einhüllenden oben könnte noch verstärkt werden, wenn man den gegenseitigen Windschatten der Tropfen in Betracht ziehen würde. Und streng genommen muss man auch die Schwerkraft und den Fahrtwind korrigierend in den Abreiß-Vorgang der Tropfen vom Reifen berücksichtigen, das Reifenprofil, die Reinheit des Wassers (Dichte und Viskosität sowie Adhäsion).
Übrigens: Da sich das Rad immer weiter rollend dreht (also ein kontinuierlicher Prozess abläuft!), darf man die Bilder nicht nur als stroboskopisch dokumentierten Zeitablauf von Flugbahnen lesen, sondern auch als Momentaufnahme nacheinander abgeschleuderter, diskreter Tropfen! Ein sehr kurz belichtetes Foto sollte also ähnliche Erscheinungen dokumentieren können.
Aber es soll hier genug sein, dann man sieht, dass
- der Rücken des Radfahrers nass wird, wenn er kein Schutzblech am Rad hat
- die Höhe der Wolke und ihre Länge mit der Geschwindigkeit zu tun haben
- bodennaher Film und „oberer Strahl“ tatsächlich entstehen
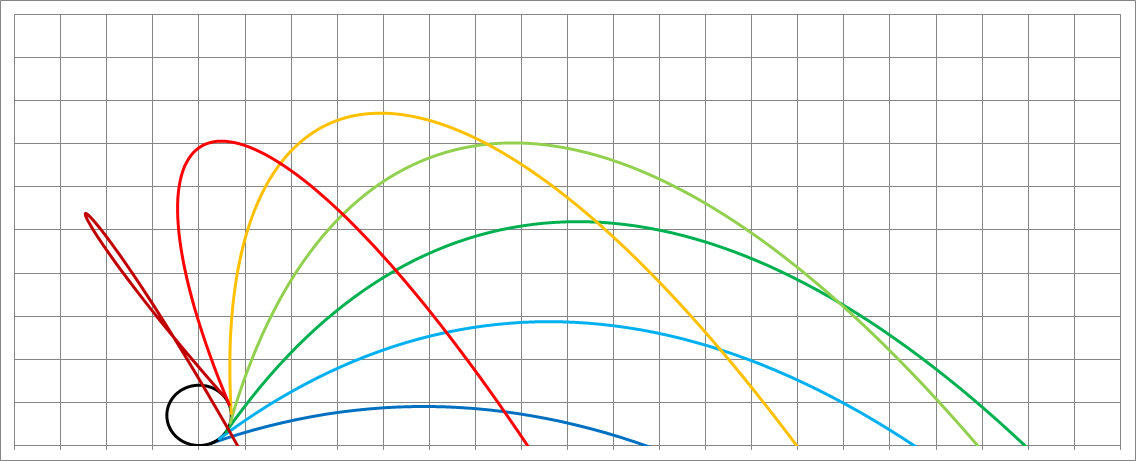
Eine kleine Ergänzung sei noch erlaubt, denn auch in der Senkrechten muss der Luftwiderstand berücksichtigt werden. Damit wird die Wasserfahne hinter dem Rad tatsächlich auf die Erfahrungswerte reduziert:
Wirkung des Luftwiderstands etwas verringert (größere Tropfen): Fontäne fast halben Meter höher, aber NICHT länger: Die größeren Tropfen schleudern (im Luftwiderstand!) zwar höher, aber fallen dafür (im Luftwiderstand!) auch schneller!
Das Spielen mit den Parametern des Programms macht einen Riesenspaß. Nachbauen!!!

Auch bergauf gibt es Fontänen, wenn man genug Kraft hat… (http://view.stern.de/de/rubriken/sport/regen-rennrad-radrennen-radsport-radrennen-02-original-1382691.html) Ein besseres Bild habe ich erstaunlicherweise nicht gefunden, dabei würde sich das im Sonnenschein nach einem Gewitter doch vor einem dunklen Hintergund irre gut machen!
Nun könnte man sogar noch die Verwirbelungen durch Fahrtwind am Reifen, Rahmen und Fahrerwaden, die Schwerkraft am Reifen usw. usf. einbauen, aber das führte zu weit weg vom grundsätzlichen Thema des Modellierens in Abgrenzung zu anderen Methoden der Veranschaulichung.
Wegen dieser Verwirbelungen bei hohen Geschwindigkeiten sind auch Bilder von Motorradrennen NICHT geeignet, das Modell zu unterstützen oder gar zu bestätigen:
https://www.motorsport-magazin.com/motogp/news-234439-interview-mit-anthony-west-motorrad-vagabund-sucht-arbeit/







Kommentar abgeben