2.8.3.1 Integration der Kugelschale
Ausführliche Erläuterung der analytischen Integration der Schwerkraft einer Kugelschale.
Jeder einzelne Massepunkt der Kugelschale übt seine eigene (nicht abschirmbare, also additiv superponierbare) Schwerkraft auf die Probemasse aus.
Die Kunst der Integration besteht nun darin, nicht eine dreifache Integration über kartesische oder über räumliche Polarkoordinaten (wird wegen der Probemasse kompliziert) vorzunehmen, sondern die einzelnen Massepunkte so zu Zwischenvolumina zusammenzufassen, dass die Integration vereinfacht wird.
Hierzu bietet sich der Kreisring an, der schon weiter oben behandelt worden ist: Alle Punkte eines Kreisringes, der senkrecht zur Verbindungslinie zwischen Kugelschalenmittelpunkt und Probemasse liegt, haben den gleichen Abstand zur Probemasse, wobei sich die senkrecht zur Verbindungslinie wirkenden Kraftkomponenten gegenseitig aufheben. Hier wird also der Kosinus des halben Öffnungswinkels eine Rolle spielen.
Der erste Gedanke ist, die Kugelschale aus Kreisringen aufzubauen, die eine konstante Abstandsdifferenz zur Probemasse haben, womit über das Differential dieses Abstandes zu integrieren wäre. Der Ringdurchmesser würde über die Kreisgleichung dargestellt werden, wobei die Ringfläche (und damit der Masse-Anteil jedes Ringes) etwas problematisch wird (in der Nähe des Pols wird die dazu erforderliche Ableitung der Kreisfunktion sehr groß). Da über die Kreisgleichung aber eine Beziehung zwischen Abstand und Durchmesser jedes Ringes besteht, bliebe tatsächlich eine Integration über eine einzige Variable übrig.
Der zweite Gedanke ist deshalb, in Polarkoordinaten vorzugehen, wobei ebenfalls nur zwei Variablen erforderlich sind, nämlich der halbe Öffnungswinkel des Ringes (vom Mittelpunkt der Kugel aus gesehen) und der Radius des Ringes, welche aber beide wieder durch die Kreisgleichung (hier durch die Winkelfunkton) aufeinander bezogen sind, weshalb hier am Ende wieder nur eine Integrationsvariable übrig bleibt.
Die Integration über den Winkel erweist sich als schwierig, weil gemischte Winkelfunktionen entstehen.
Die Integration über den Ringelement-Abstand s zwischen Probemasse und Ring hingegen erweist sich als vorteilhaft, weil darin beide Winkel stecken, nämlich die, die an beiden Enden der „Mittelpunkt-Probemasse-Seite“ des Dreiecks „Mittelpunkt-Probemasse-Ring“ liegen. Über zweifache Anwendung des Kosinus-Satzes lassen sich diese beiden Winkel auf die Dreiecksseiten zurückführen, von denen zwei fest vorgegeben sind (Kugelradius und Abstand der Probemasse) und somit allein die dritte als Variable zur Integration übrigbleibt. Da einer der beiden Winkel auch noch im Masseanteil (vermittelt durch den Ringradius) steckt, kommen überhaupt keine Koordinaten mehr vor, denn auch die Integrationsgrenzen lassen sich über die beiden festen Größen Kugelradius und Abstand bestimmen.
Festlegen der Variablen
d Probemasse-Abstand vom MP
R Kugelradius
s Abstand Probemasse-Ring-Element
r Ringradius
z Abstand Probemasse-Ring-MP
α Ring-Winkel an der Probemasse
θ Polarwinkel im Kugel-MP (d auf der Polachse)
A Kugeloberfläche
dA Ringoberfläche
m, M Kugelschalenmasse, Probemasse
dm Ringmasse
G Gravitationskonstante
F, dF Kugelschalenkraft, Ringkraft
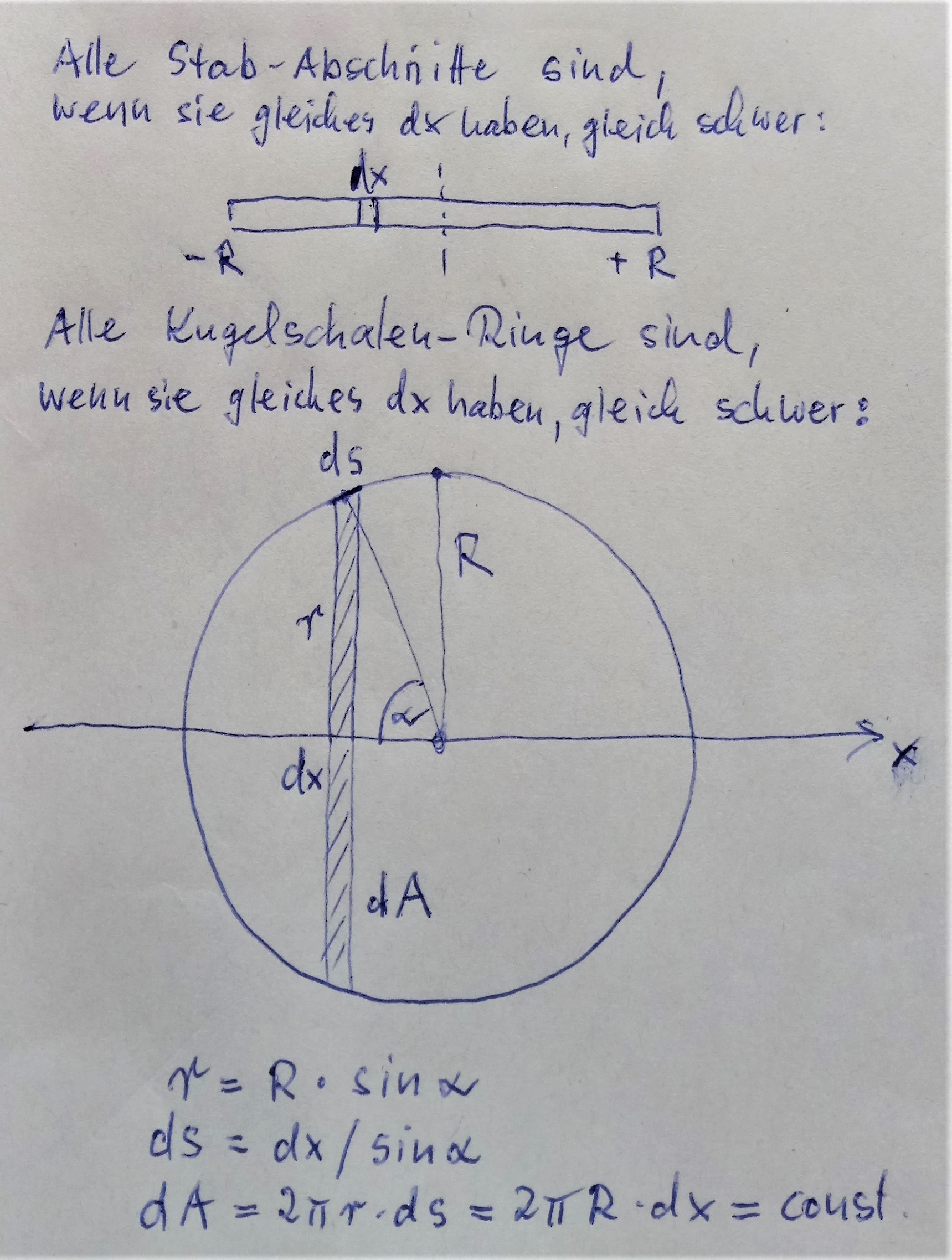
Dann gelten folgende einfache Beziehungen aus der Geometrie:
Ringradius r = R*sin(θ)
Trotzdem eröffnen sich nun zwei Wege:
a) Ringe als Teilung des Winkels θ
b) Ringe als Teilung der Achse z
a) Integration über Ringe, die den Azimut-Winkel konstant teilen
Ringoberfläche dA = 2πR*sin(θ)*R*dθ = 2πR²*sin(θ)*dθ
Ringmasse dm = dA/A*m = m/2 * sin(θ)*dθ
Kosinussatz 1 cos(α) = (s²+d²-R²)/2sd
Kosinussatz 2 cos(θ) = -(s²-d²-R²)/2Rd
Ringabstand z = d – R*cos(θ) = d + (s²-d²-R²)/2d
Das Gravitationsgesetz nimmt die Form an:
Einzelner Ring: dF = -G*dm*M/s²*cos(α) = -G*dm*M/s²*(s²+d²-R²)/2sd
Um über s integrieren zu können, muss z.B. der Kosinussatz 2 differenziert werden und ergibt die Beziehung
2s*ds = 2Rd*sin(θ)dθ -> sin(θ)dθ = s/Rd*ds
Damit kann dm neu formuliert werden:
dm = m/2 * s/Rd * ds
Die Gesamtkraft ist jetzt das Integral über alle Ringkräfte:
F = -GmM/(4Rd²) * ʃ (1+(d²-R²)/s²)ds [von d-R bis d+R]
Die Integration ergibt
F = -GmM/(4Rd²) * (s-(d²-R²)/s) [für s=d-R und s=d+R]
Grenzen eingesetzt ergibt
F = -GmM/(4Rd²) * [(d+R-(d²-R²)/(d+R))-(d-R-(d²-R²)/(d-R))]
= -GmM/(4Rd²) * [(d+R-(d-R))-(d-R-(d+R))] = -GmM/(4Rd²)*4R = -GmM/d²
und somit die Schwerkraft durch eine Masse m im Abstand d, was der Abstand des Mittelpunktes (Schwerpunktes) ist.
Dieses Ergebnis ist untrennbar mit der Winkelfunktion für die Ringmasse und mir der Winkelfunktion für den Ringelement-Abstand verbunden und gilt deshalb NUR für die Kugel, denn schon beim Rotationsellipsoid ist mindestens eine der Funktionen anders, ohne dass eine Chance auf Ausgleich besteht.
Übrigens ist schon eine numerische Rechnung mit lediglich 20 Ringen (Trapezmethode) auf 0,1 Promille genau, verglichen mit der analytischen Lösung.
b) Integration über Ringe, die die z Achse konstant teilen
Ringoberfläche dA = 2πR*sin(θ)*R*dθ = 2πR²*sin(θ)*dθ
Achsteilung dz = d(R(1-cos(θ)) = d(R-R*cos(θ)) = R*sin(θ)*dθ
Damit wird dA = 2πR*dz. Die Ringmasse ist dann bei konstanter Dicke der Kugelschale
dm = dA/A * m = dz*m/2R.
Alle Teil-Ringe der dünnen Kugelschale haben also identische Massen! Damit wird der Vergleich zu einem anderen Objekt gleicher Massen pro dz, nämlich dem dünnen Stab in Längs-Richtung, interessant. (s.u.!)
Unter Berücksichtigung der „Auslenkung“ des Einzelringes von der Achse und unter Berücksichtigung der Kugelform der Schale (y=f(z)) ergibt sich:
Fr = M*G*dm*z/(z²+y(z)²)²/³ = MGdm * z/(R²-d²+2zd)³/²
= MGdm * z/(b+az)³/² mit a=2d und b=(R²-d²)
Im Bronstein findet man dieses Integral unter Nummer 136:
ʃ(x/√X³)dx = 2/a²(√X+b/√X) mit X = ax+b, bei uns also X = az+b.
Mit Geduld und Spucke lässt sich das für die Integrationsgrenzen z=d-R und z=d+R ausrechnen:
F = GMdm * 2/(4d²)*(+ (R²-d²)/√(2dz+R²-d²) ) [Grenzen einsetzen]
= GMdm /(2d²) * [(√(2d(d+R)+R²-d²) + (R²-d²)/√(2d(d+R)+R²-d²) ) – (√(2d(d-R)+R²-d²) + (R²-d²)/√(2d(d-R)+R²-d²) )]
= GMdm /(2d²) * [((d+R)+(R-d)) – ((d-R)-(R-d))]
= GMdm*4R/(2d²) = GMm/d² q.e.d. (mit m=dm*2R)
Das wäre also geschafft. Die Lösung des Integrals hatte übrigens die gleiche Form wie unter a).
Numerisch ist das auch zu ermitteln, da kann man die Beiträge der einzelnen Ringe grafisch darstellen und mit dem längs liegenden Massering und seinen Elementen, den „Doppel-Punkten“, vergleichen (siehe 2.8.3 ziemlich weit unten). Viel anschaulicher ist aber der Vergleich mit dem längs liegenden dünnen Massestab, dem die gleichen Massen pro dz zugeordnet werden sollen, dem aber die Aufhebung gegenüberliegender Kraftkomponenten fehlt:
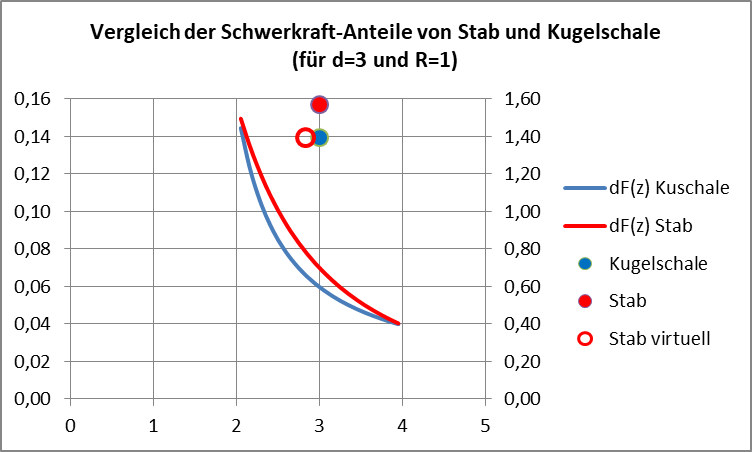
Vergleich des Verlaufs der differentiellen Kraft der gleichschweren Elemente von Kugelschale und Längs-Stab als Funktion des Abstandes von der Probemasse (der Stab folgt der Kraftgesetz-Hyperbel, die Kugelschale liegt darunter)
Man sieht, dass das Integral für die Kugelschale (blauer Punkt im Schwerpunkt-Abstand) deutlich geringer ist als das des Stabes (roter Punkt im Schwerpunkt-Abstand). Der relative Unterschied ist eine Funktion des Verhältnisses von R und d. In diesem Fall wäre das „Virtuelle Schwerezentrum“ um 5,7% dichter an die Probemasse gerückt, also bei z=2,83 statt bei z=3,00. Der Ort einer Punktmasse gleicher Schwerkraft-Wirkung wie beim Stab läge also im roten Kreis.
Im Inneren der Kugelschale ergibt sich übrigens ein kraftfreier Raum. Das kann man auch mit einfachen Symmetrieüberlegungen zeigen.
Nimmt man einen beliebigen Punkt im Inneren der Kugelschale an, so kann man durch diesen eine beliebige Gerade legen, die die Kugelschale zweimal schneidet. Um diese Gerade herum denkt man sich einen schmalen Kegel, der aus der Kugelschale zwei ellipsenähnliche Stücke schneidet, deren Flächen dem Quadrat ihrer Abstände vom gedachten Punkt proportional sind. Dafür brauchen wir die Bedingung, dass beider Flächen Winkel zur Geraden identisch sind, was aus der Symmetrie des Kreises/der Kugel zwingend folgt. Die Flächen entsprechen den Massen der ausgeschnitten Kugelschalenstücke, deren Schwerkraft wiederum quadratisch mit dem Abstand sinkt.
Die beiden quadratischen Abhjängigkeiten heben sich gegenseitig auf, womit die beiden Kräfte gleich groß und entgegengesetzt sind und ihre Resultierende Null ist. (Das gilt genau und nur für den Kraft-Exponenten -2! In allen anderen Fällen gibt es also wieder Rosetten als Trajektorien, selbst wenn die Zentralmasse eine Kugel ist…)
Da das für jeden beliebigen Punkt und jede beliebige Richtung der Geraden gilt, ist der gesamte Innenraum kräftefrei. In der Folge ergibt sich für eine Vollkugel eine lineare Abhängigkeit der Schwerkraft vom Abstand zum Mittelpunkt im Inneren und die bekannte reziprok quadratische im Äußeren.
Es gibt noch einen zweiten, aber rein theoretischen Fall der Kräftefreiheit, und zwar den zwischen zwei parallelen Ebenen gleicher Massedichte:
Das ist deshalb „Theorie“, weil es unendliche Ebenen nicht gibt. Im Grenzfall „Abstand klein gegen Ausdehnung“ gilt es genähert dann doch.
Bildet man drei Paare paralleler Ebenen (im einfachsten Fall einen Würfel), so ist im Innenraum nur ein einziger Punkt kräftefrei, weil im allgemeinen Fall die Geraden, die nichtparallele Ebenen schneiden, für Unsymmetrien sorgen, die sich nicht aufheben können. Insbesondere wird in der Nähe der Ecken die Schwerkraft größer, weil der Anteil der „nichtparallelschneidenden“ Geraden größer wird. (Bild als gute Übung selber malen!)