Kristallografie
(letzte Änderung: 14.06.2023)
Die Kristallografie behandelt die logischen Zusammenhänge zwischen den Kristallformen aus geometrischer Sicht und bezieht sich natürlich auf physikochemische Grundlagen und nutzt mathematische Methoden.
Es ist eine lange historisch gewachsene Wissenschaft und ist deshalb vielen alten Begriffen und didaktischen Methoden verpflichtet und ist eng an die Mineralogie gebunden.
Hier wird vorgeschlagen, den didaktischen Zugang zur geometrischen Komponente etwas zu verändern, nämlich vom ursachenfreien schrittweisen „Aufbau“ der Symmetrien vom Chaos zur Ordnung zum ursachengebundenen „Abbau“ der natürlichen Symmetrie dichtestgepackter Kugeln zu realen Kristallen als zur ursachengebundenen Ordnung überzugehen, denn:
Wenn man bei der Entwicklung der Systematik der Kristallformen von dem Fall ausgeht, der die wenigsten Einschränkungen erfordert, der also der allgemeinste ist, so muss man sich zuerst fragen, was man unter „Einschränkung“ versteht: Einschränkung des Chaos oder Einschränkung der Ordnung?
Die Chaoten beginnen also rein geistig-mathematisch mit dem Fall niedrigster Abweichung vom Chaos, mit der niedrigsten Symmetrie (triklin), um sich schrittweise zu „höherer“ Ordnung bis zum kubischen System durchzuringen. Die Ordentlichen (wieso gibt es dafür keinen so klaren Eigenbegriff? Wär „die Kausalen“ gut?) oder Naturliebhaber gehen von der höchsten Ordnung als energetischem Normalfall aus und arbeiten sich zu den einschränkenden Abweichungen vor, die ja schließlich einen „Grund“ haben müssen. (Dazu gehöre ich.)
Die „grundlose“ Ordnung als Ausgangspunkt wäre, Kugeln (Objekte höchster und einfachster dreidimensionaler Symmetrie) zu schütteln, bis sie sich zur dichtesten Packung geordnet haben; dann liegen sie alle in Ebenen „auf Lücke“ und die Ebenen untereinander auch. Man findet schnell, dass die Ebenen zwei Möglichkeiten der Schichtung haben: ABA oder ABC.

vorsichtig geschüttelte Stahlkugeln wechseln ihre Plätze in Richtung des potentiellen Energieminimums
Wir haben „regelmäßige Sechsecke mit Mittelpunkt“ vor Augen oder „gleichseitige Dreiecke“, je nach bevorzugter Sichtweise. Nehmen wir ein solches Sechseck heraus, hat die nächste Schicht zwei Möglichkeiten, drei Kugeln auf die sechs Lücken zischen Mittelpunkt und Peripehrie eines Sechseckes zu verteilen. Daraus ergeben sich die zwei Schichtungsmöglichkeiten ABC oder ABA, und jedesmal hat eine Kugel sechs Nachbarn in der gleichen „Auf-Lücke-Ebene“ und je drei darüber und darunter.
(Weiter zu sehen: Der Rand der Anordnung erzeugt in seiner Nähe „Unordnung“. Es können auch einzelne Kugeln „herumliegen“, die sich (noch?) nicht einer neuen geschlossenene Schicht angeschlossen haben.)
Aber nun geht es schon los mit der Erfordernis von begrifflichen Festlegungen, wenn man erfolgreich Gedanken austauschen will:
Die Schichtung ABC nennen wir „kubisch dichteste Kugelpackung“, weil sie exakt der Anordnung der 8 Kubusecken entspricht, wenn man den Würfel (=“Kubus“) in seiner Raum-Diagonalen-Richtung betrachtet (das sieht man am besten natürlich in einer 3-D-Darstellung, dazu muss man aber das Schielen „durch die Betrachtungsebene hindurch“ geübt haben):

Würfel von der Ecke her (absichtlich ganz leicht gekippt) betrachtet: die drei Nachbarn der vorderen Ecke liegen in einer Ebene, die drei der hinteren auch, aber auf Lücke, und die vordere und hintere Ecke liegen übereinander, aber zu beiden anderen Ebenen je auf Lücke: ABCA=“ABC“
(Es kann sein, dass je nach Bildschirmeinstellung ein Zoom bei der Betrachtung helfen kann. Beim „richtigen“ Schielen überlagern sich zwei der vier Bilder so, dass das mittlere der drei verbleibenden Bilder räumlich erscheint und hinter – beim Fernschielen – oder vor – beim Nahschielen – der Bildschirmebene zu schweben scheint.)
Die Schichtung ABA ist dann eine „hexagonal dichteste Kugelpackung“.
(Streng mathematisch kann man nun von gruppentheoretisch behandelbaren „Raumgruppen“ ausgehen, aber das führt hier zu weit.)
Immer hat also eine Kugel bei dieser dichtesten Packung 12 Nachbarn. In der Natur kommt das vor, wenn man feste Kugeln mechanisch schüttelt, wenn man Seifenblasenschaum konstanter Blasengröße macht (das sind dann natürlich keine „Kugeln“), wenn Laich nicht „in Schnüren“ abgelgt wird, und wenn Atome nicht auf Bindungsanzahl achten müssen (viele reine Metalle im „Elektronengas“).
Sieht man auf die obige Abbildung, so existieren beim reinen kubischen Gitter aber immer nur 6 Nachbarn! Was ist hier falsch? Wir müssen die Flächenmittelpunkte (durch schwache graue Linien angedeutet!) mit hinzurechnen. Davon gibt es in der ersten Ebene (nach „unten“ oder „hinten“, jenach Anschuung) drei Flächenmitten neben den drei Würfelecken (alle 6 durch eine ebenes graues Dreieck verbunden) und in der nächsten ebenfalls. Nun stimmt die Zahl der Nachbarn, und das jetzt „richtige“ Gitter nennt man „kubisch flächenzentriert“. Der kürzeste Abstand zwischen zwei Nachbarn ist jetzt eine halbe Flächendiagonale des Würfels und kommt für jeden Punkt 12 mal vor. Bitte selbständig nachzählen und in Gedanken immer die Nachbarwürfel mit einbeziehen – das ist anfangs schwer, klappt aber nach etwas Übung entweder von der Anschauung her oder rechnerisch in verschiedenen Ansätzen:
- an jeder Ecke treffen sich acht Würfel mit je drei benachbarten Flächenmitten, von denen je zwei identisch sind, macht 12 Nachbarn
- von jeder Flächenmitte aus gibt es vier benachbarte Ecken und zwei mal vier benachbarte Flächenmitten (oben und unten), macht 12 Nachbarn
Nun beginnen wir mit der systematischen Einschränkung der absoluten „Ordnung“, indem wir den Elementen Eigenschaften geben, die von denen der einfachen Kugel abweichen. Wenn sie nur noch 8 Nachbarn vertragen, wird im kubischen System das raumzentrierte, wenn nur 6, das primitive Gitter. (Gründe liegen in der Elektronenkonfiguration, die hier nicht das Thema ist).
(Betrachtung aus der reinen Sicht der Eckpunkte als Schnittpunkt von 3 oder mehr Flächen siehe unter Elemente der Geometrie – Punkt als Kreuzung!)
Weitere Einschränkungen liegen dann darin, dass wir Moleküle zulassen. Dann könnte die Würfelfläche nicht mehr vierzählige Rotationssymmetrie aufweisen, sondern vielleicht nur zweizählige (Pyrit). Hier beginnt die Fabelwelt der Mineralogie oder Stereochemie. Man erkennt solche Einschränkungen natürlich nicht an der Idealgestalt des Würfels, denn Würfel ist Würfel ist Würfel. Da aber beim Wachstum auch regelmäßige „Treppen- und Ecken-Strukturen“ auftreten können, wie man schon als Kind mit Bauklötzern durch Trial and Error gelernt hat, ist das Ergebnis sehr wohl davon abhängig, ob man Würfel („Einer“) oder „Zweier“ oder „Dreier“ geschichtet hat.
Für solche zusammengesetzte Flächen haben die Kristallografen ein System der Beschreibung erfunden, das sehr praktisch ist: Die Neigungsverhältnisse der Flächennormalen gegen die drei Koordinatenebenen wird mit kleinen ganzen Zahlen ausgedrückt, den „Millerschen Indizes“ (Selbststudium probieren!!). Lauten die Achsen x, y und z, so bedeutet dann (100) Parallelität zur x-Achse (bzw. senkrecht zur y-z-Ebene), (110) die Flächendiagonale der xy-Ebene und (111) die Raumdiagonale. Die (012)-Fläche des Pyrits ist dann 26,6° (arctan(1/2)) gegen die x-y-Ebene geneigt und ein leicht vom regelmäßigen abweichendes Fünfeck mit Symmetrieachse. Ein regelmäßiger Körper, der nur aus diesen Flächen entsteht, ist ein Pyritoeder und ähnelt dem platonischen Pentagon-Dodekaeder (dort ist der Winkel nach dem Goldenen Schnitt 31,7° = arctan(0,681)):
(eigenes 3D-Programm)
Hier ist nicht der Platz, dieses Denksystem komplett zu vervollständigen (dazu siehe bitte die externe Abhandlung „Kristallsymmetrie neu gedacht“), aber trotzdem muss im Zusammenhang mit dem entsprechenden Abschnitt zum Wachstum der Grenzfall erläutert werden:
Lässt man also zu, dass alle drei Millerschen Indizes von Null verschieden und untereinander verschieden sind, so ergeben sich (negative Indizes zugelassen) als Maximum 48 Permutationen, was einem regelmäßigen Körper mit 48 Flächen „des gleichen Typs“ entspricht, die zu je acht in jede Achsrichtung (positiv und negativ) zeigen.
Nun kann man die Symmetrie schrittweise einschränken und eine Tabelle machen, in der alle grundsätzlichen Kombinationen der Millerschen Indizes vorkommen. Das sieht dann in Stereo-Darstellung so aus (rechts oben die höchste Symmetrie, links unten die geringste; habe mir Mühe gegeben, jedesmal ungefähr den gleichen Blickwinkel beizubehalten):

Für die Freunde der umgekehrten Denkrichtung gibt es im kubischen System auch die Anwendung der Symmetrieoperationen auf den Würfel bis hin zum 48-Flächner:
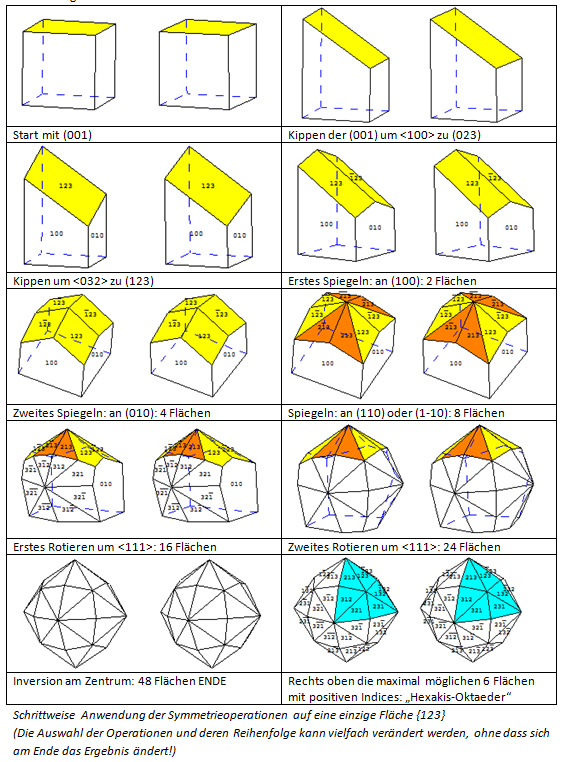
(Hier ist das Programm „Shape“ genutzt worden.)
Jeder Mineraliensammler weiß, dass es spannend wird, wenn erstens mehrere Flächentypen gleichzeitig vorkommen und zweitens die Isometrie gebrochen wird, das heißt, die Kristallformen „verzerrt“ sind, also in verschiedenen Raumrichtungen unterschiedlich gedehnt oder gestaucht sind.
Diese schier unendlich wirkende Vielfalt lässt sich in Übergangsreihen demonstrieren, wo jede Mischform als Übergang zwischen reinen Formen verstanden werden kann:

(Hier wieder mein eigenes 3D-Programm.)
Hat man das begriffen, kann man komplexe Kristall-Schönheiten mit mehreren Flächentypen und Verzerrungen verstehen und „nachbauen“:

Seltenes Pyrit-Exemplar mit 4 Flächen-Typen (-Indizierungen)
Theorie-Einschub:
Übrigens ist dieser konkrete Kristall ein schönes Beispiel für Serien paralleler Kanten (Zonen) im Zusammenhang mit den Millerschen Indizes der dazugehörigen Flächen: Die eingeschlossene Fläche ergibt sich (ggf. gekürzt) über die Summe der einschließenden, z.B. 001 (Würfel) + 111 (Oktaeder) = 112 (Deltoid-Ikosatetraeder) oder (-1)12 (Deltoid-Ikosatetraeder) + 112 (Deltoid-Ikosatetraeder) = 012 (Pentagon-Dodekaeder) oder (-1)(-1)2 (Deltoid-Ikosatetraeder) + 112 (Deltoid-Ikosatetraeder) = 001 (Würfel) oder 0(-1)2 (Pentagon-Dodekaeder) + 012 (Pentagon-Dodekaeder) = 001 (Würfel). Die eingeschlossene Fläche ist dann eine parallel abgefaste Kante der einschließenden beiden (es ergäbe sich beim umgekehrten Prozess des Abfasens also ein kantenabgestumpfter Körper). Wächst sie – die Fase – anschließende wieder „heraus“, berühren sich die einschließenden wieder zum einfacheren Körper.
Spannend ist es, verschiedene Flächen des kubischen Systems einmal aus Würfel-Elementarzellen selber zusammenzubauen, zum Beispiel für den Typ (hkk) die (211) oder für den Typ (hhl) die (221): Hier nimmt man die reziproken Millerschen Indizes als kartesische Achsabschnitte (kehrt also einfach ihre Definition um) , legt diese mit Würfeln aus und füllt sukzessive die (i.a. schiefe) dreiseitige Pyramide aus (erfordert etwas Geduld und Geschick, hilft der Anschauung aber ungemein!):

Hilfreich ist auch, sich die Millerschen Indizes als Komponenten des Normalenvektors (hier im kubischen System alle 90° zueinander und die Einheiten gleich lang!) vorzustellen, denn dadurch ist die Symmetrie der Normalen zu den Achsen klar erkenntlich: Bei beiden linken Modellen muss die Normale in der Ebene der Winkelhalbierenden von x- und y-Achse und der z-Achse liegen, im rechten Modell dagegen in der Ebene der Winkelhalbierenden von y- und z-Achse und der x-Achse. Ihre „Steilheit“ innerhalb dieser Ebene wird durch den dritten Index angegeben. Die Normale zeigt dann immer am meisten in Richtung des höchsten Index, zwei gleich große somit in die Mitte zwischen beiden.
(Auf diese Weise kann man die Indizes und ihre Nützlichkeit besser „verstehen“ lernen als durch die neuerdings modern und üblich gewordenen Handlungsanweisungen bei „YouTube“ zur Berechnung der Indizes, wo z.B. neun stupid abzuarbeitende Schritte genannt werden, ohne jemals über Zusammenhänge zu informieren oder diese gar herzuleiten, nach deren Verständnis man ja selber handeln könnte…)
Hier noch zwei Holzwürfel-Beispiele mit mehreren Flächen zum Selber-Bestimmen:


Auflösung für Ungeduldige: x-Achse nach rechts, y nach oben, z zum Betrachter:
Beide Beispiele enden am Dach mit der (001), links davon die (-101), rechts davon die (102), nach unten die (0-11), links unten die (-1-11).
Oberes Bild: Rechts unten die (1-22)
Unteres Bild: Rechts unten zusätzlich noch ganz rechts als kleiner Übergang die (1-11).
Zurück zum Pyrit mit den vier Formen (100) Würfel, (111) Oktaeder, (210) Pentagon-Dodekaeder und (211) Drachenviereck-Ikosatetraeder :
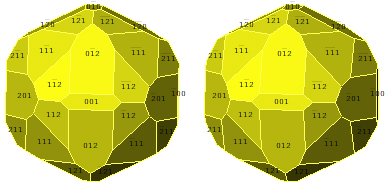
Nachbau fast isometrisch (zeigt wegen fehlender Individual-Verzerrung teilweise andere Eckenzahlen der einzelnen Flächen als das natürliche Original)

Äquidistanter (d.h. identische Zentralabstände) Nachbau des 4-Formen-Pyrits: Weist durch die große Ähnlichkeit mit dem Tansanier im Umkehrschluss auf außergewöhnliche Wachstumsbedingungen des Originals hin!
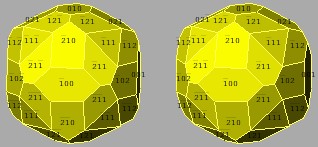
Hier eine Verschiebung zu minimaler Eckenzahl, (111) mit drei vierzähligen Ecken, Kristall aus Versehen um 90° gedreht (x-Achse nach hinten)

Draufsicht: Hier ist jetzt der Kopf des isometrischen 4-Typen-Kristalls aus Würfelchen nachgestellt, wobei die (211) etwas geschickter gelegt worden ist, so dass ihr Übergang zur (111), links vorn, schön ersichtlich wird. Auch die (100) oben und die (210) rechts vorn sind „fließend“ mit der (211) ineinander übergehend. Fingerspitzengefühl ist bei den sejr leichten Würfeln (knapp 10 mm großes Montessori-Material) gefragt… Wer Lust hat, baut daraus ein komplettes isometrisches Modell, neue Raffinessen werden aber nicht mehr auftachen! Die (210) wird dann vorn spitz auslaufen.

Die 5 Schichten zeigen rechts oben (und auch in den drei anderen Richtungen) in den oberen drei die (211) und in den unteren drei die (111). In den Zwickel zwischen (012) und (111) müsste die (121) gelegt werden, aber dafür bräuchte man eine weitere Würfelchenschicht… (noch mehr Fleiß erfordelich!)

Vorderansicht

Schrägsicht
Übrigens sind an diesem Exemplar auch die Vizinalflächen (Waschstums-Pyramiden) in der jeweilgen Rotations-Symmetrie-Zahl der dazugehörigen Fläche zu sehen:

111 (dreizählig) hat deutliche „Mercedes-Stern“-Dreiecke (Flächenform z.B. als Fünfeck 2*60°, 150°, 2*90°)

210 (Spiegel) hat elliptische doppel-biberschwanzartige „Blasen“ (Flächenform z.B. Siebeneck 2*90°, 2*24°, 2*29°, 73°)

211 (Spiegel) zeigt „dachziegelartige“ Ausstülpungen deformierter Dreiecke (Flächenform z.B. als Fünfeck 51°, 51°, 129°, 68°, 61°)
Die vier Flächen-Typen des Pyrit-Kristalls mit ihren Vizinal-Hügeln, an denen man die Symmetrieeigenschaften der jeweilgen Fläche wiederfindet. Deren Ausprägungsform hängt von den Zentralabständen der Nachbarn ab.
Nun ein paar andere Mineralien, die interessante Flächen ausbilden:

Aquamarin aus Pakistan

Rauchquarz aus dem Val Giuv nahe der Rheinquelle

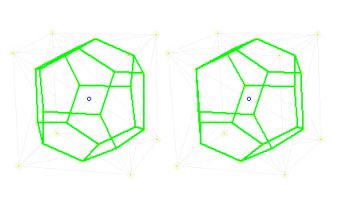
Spiel mit dem Drachenviereck-24-Flächner (Deltoid-Ikositetraeder ITE) am Beispiel von drei Kristallen aus meiner Sammlung: zwei fast ideal, einer verzerrt (Spessartin)
Für alle die, die nicht selber weiter überlegen oder rechnen oder recherchieren wollen, hier ein paar Bilderchen zur Anregung zu den Kristallsystemen und einzelnen Mineralien:
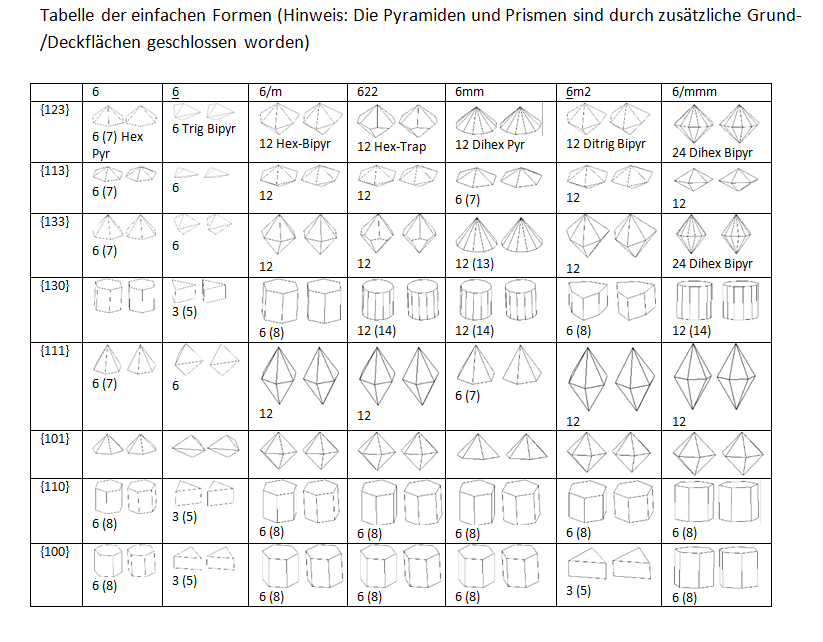
Hexagonales System

Trigonales System

Tetragonales System

Rhombisches System
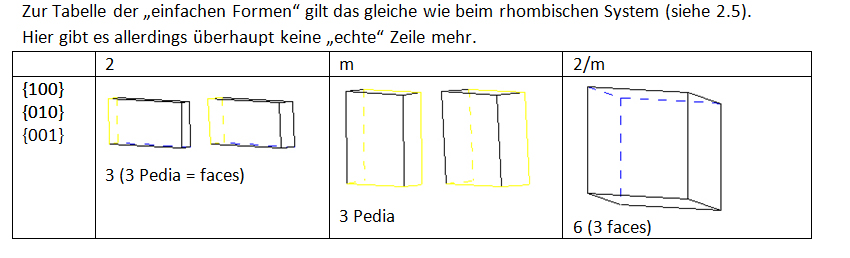
Monoklines System

Triklines System

Hämatit, wie er länglich in „Zahnform“ neben dem Baryt im Erzgebirge vorkommt

Rauchquarz aus der Schweiz (als ich dort war, war schlechtes Wetter – gekauft) und Calcit als Beispiel guter Zonenbildung (an parallelen Kanten) zu erkennen

Kupfersulfat aus meiner Schülerzeit

Zuckerkristall aus unserem Löwenzahnhonig

Turmalinkristall mit Endflächen, wie er in Afrika nicht selten ist
Nun wird man verstehen, weshalb es in dieser Abhandlung einen großen Abschnitt über die morphologische Stabilität beim Wachsen von Kristallen gibt und warum man beim gleichzeitigen Wachsen und Auflösen zur Gesteinskunde der kristallinen Gesteine kommen muss.
Neben dem geometrischen Aspekt gibt es aber noch den chemischen, der entsprechend der Valenzen der beteiligten Atome bestimmte Nachbarschaftsbeziehungen innerhalb des Moleküls und innerhalb der Elementarzelle (und damit das Kristallsystem und die Kristallklasse) vorgibt, und den physikochemischen, der die Umgebungsbedingungen des Wachsens oder Auflösens einbezieht, also berücksichtigt, welche „schrägen Stapelungen“ (treppen- und eckenförmig mit bestimmten Verhältnissen, ausgedrückt mit den Millerschen Indizes) thermodynamisch wahrscheinlich und also stabil sein können, um reine, gemischte, verzerrte usw. Formen zu ermöglichen.
Dabei ist der dynamische Aspekt von überaus wichtiger Bedeutung, dass beim Wachstum diejenigen Flächen, die in Richtung ihrer Normalen AM LANGSAMSTEN wachsen, am Ende übrigbleiben, weil die anderen aus der Hüllform „herausgewachsen“ sind. (Bei der Auflösung ist es umgekehrt, was angelöste Objekte für den Sammler begehrt machen kann.) Man kann sich das am einfachsten mit einem regelmäßigen Achteck klar machen, indem man die vier „schrägen“ Flächen doppelt so schnell nach außen wandern lässt wie die „geraden“ (bzgl. der rechtwinkligen Achsen gemeint). Daraus folgt die bewährte Betrachtungsweise und die Konstruktion der verzerrten Formen über ihren so genannten „Zentralabstand“: Je kleiner dieser ist, desto größer wird i.a. die dazugehörige Fläche sein. (In der zweidimensionalen Version könnte man jede Umhüllungs-Ebene als Gerade zeichnen und den real existierenden Kristall mit dem kreuzungsfreien Innenraum festlegen:

Die (12) hat sich durch große Wachstumsgeschwindigkeit aus dem Kristallbereich selbst verabschiedet. Das kann später auch mit der (11) passieren.
In Mehrstoffsystemen wird dann klar, dass derjenige, der zuerst kommt, die besten Grenzflächen ausbilden kann und der letzte dann die Zwickel füllen muss. Das wissen die Gesteinskundler wie die Metallurgen, nur dass letztere mit anschließenden Prozessen das Gefüge noch ändern können und müssen. Bei beiden spielen spätere Transportprozesse (z. B. an den Korngrenzen) eine große Rolle.


Kommentar abgeben