2.8.3.2.1 Spezialfall: gerader radialer „Fall“ des „Sonnensturzes“
Es ist eine schöne Übung, die Kepler-Ellipse einmal „entarten“ zu lassen: Man setze die Kleine Halbachse auf Null und schaue, was passiert:
Die sich nur nach dem Gravitationsgesetz bewegende vernachlässigber „kleine“ Masse stürzt geradenwegs auf die „große“ zu und dann?
Mathematisch könnte sie über diese hinwegschwingen, ohne anzustoßen, physikalisch aber würde sie zerschellen, verdampfen oder usw.usf.
Schwingt sie aber tatsächlich mathematisch darüber hinweg?
Sieht man sich die Kepler-Ellipsen gleicher Großer Halbachse an und erhöht ihre Exzentrizität (verringert als die Kleine Halbachse), so wächst die Apoapsis auf Kosten der Periapsis, bis letztere zu Null wird. Dann ist die Bahn wie eine „Reflexion“ an der Zentralmasse (sie „knallt“ also ans gegenüberliegende Ufer des Potentialtopfes und wird zurückgeworfen). Die Umlaufzeit aber ist nach „Kepler 3“ konstant geblieben, da dort die Kleine Halbachse gar nicht vorkommt.

Man denke sich die rechte braune Ellipse weiter zusammengedrückt und zu eine Strecke der gleichen Großen Achse „entartet“, deren linker Endpunkt im schwarzen Schwerpunkt liegt.
Dieser Gedanke der „Reflexion“ lässt sich auch auf den allgemeinen Fall der Kepler-Ellipse erweitern, indem man sich nur auf die Koordinate der Apsidenlinie beschränkt und die „halbe Runde“ der Periapsis als „weiche“ elastische Reflexion betrachtet. Der Vergleich mit einem in der Größe variierenden hohlen Gummiball, der im Gravitationsfeld von einer Ebene elastisch reflektiert wird, bringt in der Analyse sehr ähnliche Ergebnisse im Vergleich zur obigen Ellipsenschar incl. ihrer Entartung!
Man erkennt die Ähnlichkeit der Zeitabhängigkeiten: links der Ball bei konstanter Schwerkraft, mittig der Ball bei „echter“ abstandsabhängiger Gravitation, rechts die Apsidenkoordinate von Kepler-Ellipsen!
Für den konkreten Fall des Gedanken-Experiments, einmal auf der Erdbahn „anzuhalten“ und im freien Fall der Sonne direkt auf gerader Linie („radial“) ikarusgleich entgegenzustürzen, kann man also drei Lösungswege einschlagen und ihre Ergebnisse vergleichen:
a) Kepler 3
b) numerische Integration
c) analytische Integration
zu a) Nach Kepler 3:
(T1/T2)² = (a1/a2)³
ergibt sich, dass bei Halbierung der Großen Halbachse (der Sturz zur Sonne ist nur die Hälfte des Durchmessers der näherungsweise als Kreis gedachten Erdbahn!) die Umlaufzeit nur noch die Wurzel aus (1/2)³ = Wurzel aus 1/8 von der anfänglichen Umlaufzeit wäre. (Bei gleicher großer Halbachse und gleicher Umlaufzeit wäre der Sturzbeginn bei doppeltem Erdbahnradius!) Der Sturz ist aber nur ein halber Umlauf, also ergibt sich als Sturz-Zeit die Wurzel aus 1/32 der Umlaufzeit von einem Jahr. Das sind etwa 64,5 Tage.
zu b) Taktet man die numerische Integration fein genug in der Zeit (konstanter Stützstellenabstand), so erhält man mit der bekannten Schleife
Anfangs-Ort -> Anfangs-Kraft -> (Beschleunigung -> Geschwindigkeitsänderung -> Ortsänderung -> neue Kraft)
ebenfalls etwa 64,5 Tage:
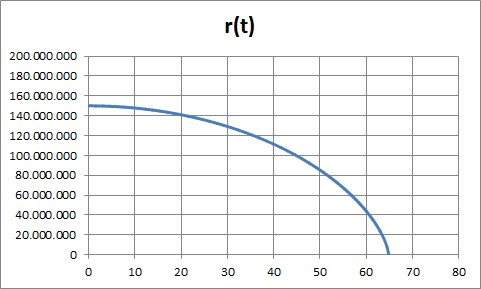
Sonnenabstand (km) als Funktion der Zeit (Tage)
zu c)
c1: Mit dem Energiesatz kann man die Geschwindigkeit (in der kinetischen Energie enthalten) mit dem Abstand (in der potentiellen Energie enthalten) verknüpfen und erhält
v = √(2GM)*√(1/r-1/R) = √(2GM/R)*√((R-r)/r)
(G: Grav.-K., M: Zentralmasse Sonne, R: Startabstand Erdbahnradius, r: betrachteter Abstand)
c2: Die Zeit lässt sich als Wegintegral der reziproken Geschwindigkeit schreiben:
Schule: t = s/v -> allgemein -> t(r) = ʃ(dr/v(r))
c3: Eingesetzt ergibt sich:
t = √(R/2GM)* ʃ(dr/√(r/(R-r)))
mit der Lösung (in Profi-Tabellen unbestimmter Integrale nachschlagen, z.B. Bronstein/Semendjajew Nr. 151 mit Substitution aus Nr. 146!)
t = √(R/2GM)*(R*arctan(√((R-r)/r))+√(r*(R-r)))
und eingesetzt wiederum mit 64,5 Tagen.
Welcher der drei Wege der „überzeugendste“ oder „gangbarste“ ist, ist Geschmacksache. Schön aber ist es in jedem Fall, dass die Ergebnisse übereinstimmen!
Das Ergebnis liegt in der Nähe von 2/3 des „realen“ vierten Teils eines Erdumlaufs. Dass das keine Einladung zum „Abkürzen“ ist, musste schon Ikarus erkennen…



Kommentar abgeben