2.8.7 Trajektorien innerhalb rotationssymmetrischer Masseverteilungen
Kann man nach allen vorangegangenen Überlegungen Aussagen zu Trajektorien im Inneren von Masseverteilungen, zum Beispiel Galaxien, treffen?
(vgl. auch 2.8.6.3.2, dort etwas ausführlicher an Spezialfällen behandelt!)
Dazu gehen wir wieder induktiv vor, oder, besser gesagt, vom Einfachen zum Komplizierten.
Betrachten wir den einfachsten Fall einer rotationsellipsoidischen Galaxie mit konstanter Massedichte. Wie unterscheidet sie sich in ihrem Inneren vom bekannten Inneren einer homogenen Kugel? (Dort haben wir einen linearen Kraftverlauf in radialer Richtung festgestellt.)
Man kann noch weiter gehen und ein echtes 3-Achs-Ellipsoid (also ohne Rotationssymmetrie!) betrachten:
Nimmt man sich wieder eine numerische Kraft-Integration vor und untersucht den Kraftverlauf entlang der Achsen sowie der Flächen- und Raum-Diagonalen des Achsenkreuzes, so staunt man nicht schlecht, dass auch hier längs einer Ursprungsgeraden eine Proportionalität zwischen Kraft und Abstand vom Schwerpunkt besteht!

Kraftverlauf innerhalb und außerhalb eines NICHT rotationssymmetrischen Ellipsoids: Im Inneren mit unterschiedlichen Anstiegen linear, im Außenraum hyperbelartig mit heftigen Offsets in der Abszisse
Was heißt das?
Das bedeutet erstens, dass
- im Falle eines Rotationsellipsoids sekrecht zur Achse in der Ebene mit dem Mittelpunkt ein „echt elastisches“ Verhalten (mit richtungsunabhängiger „Federkonstante“) erwartet werden kann: Eine elliptische Schwingung mit dem Schwerpunkt als Mittelpunkt und einer abstandsunabhängigen Frequenz. (Der Sonderfall des Kreises ist selbstverständlich Element der Lösungsmenge!)
- im Falle eines 3-Achs-Ellipsoids in jeder beliebigen Ebene durch den Mittelpunkt ein „komplexes elastisches“ Verhalten erwartet werden muss, nämlich eine Rosette als nichtsynchrone Schwingung um den Mittelpunkt mit einer neigungsabhängigen Frequenz, Winkelgeschwindigkeit und Umlaufzeit.
Das bedeutet zweitens, dass auch bei einer Neigung gegen die Rotationsebene im Rotationsellipsoid Rosetten (also Präzessionen sowohl der Apsiden als auch der momentanen Bahnebene) entstehen, weil der Gradient der Kraft zwar pro Richtung konstant, aber trotzdem winkelabhängig (also richtungsabhängig) ist.
Die Konsequenzen für eine Galaxis sind (nicht vergessen: alles ist hier NICHTrelativistisch gerechnet!), dass die sturen Erwartungen, alles bewege sich nach Keplerschen Sätzen um eine alles überstrahlende Zentralmasse, nicht in Erfüllung gehen können. Das kann man also auch schon ohne eine „Modifizierte Newton-Dynamik“ („MOND“) voraussagen, dass das T²-a³-Gesetz dann nicht zutreffen kann!
Nimmt man noch die Überlegungen zu den Stabilitätsbedingungen in den Lagrange-Punkten hinzu, muss man feststellen, dass
- zufällig auf genäherten Kreisbahnen befindliche Objekte in der ellipsoidischen Galaxis ähnliche Umlaufzeiten haben können
- eine Selektion stattfinden kann (Hinausschleudern mit Verdünnung der Galaxis oder Verschlucken im wachsenden Zentrum), die entweder den synchronen Zustand stabilisiert oder den Keplerschen um ein Schwarzes Loch erzeugt
- sämtliche Zwischenzustände möglich sind
insbesondere, wenn man bedenkt, dass die Galaxien seit dem Urknall noch nicht wirklich viele Rotationen hinter sich haben.
Des weiteren fallen entfernte Ähnlichkeiten zu Bewegungen des (allerdings inkompressiblen!) Magmas im Erdinneren auf: Betrachtet man nämlich alles im mitrotierenden System, kommen die interessanten Effekte der Coriolis-Kraft hinzu (die zu nichts anderem „führen“ als den Ellipsen im ruhenden KS). Unter diesem Aspekt kann man dann auch von Nichtgleichverteilungen der Masse innerhalb der Galaxis und ihren Auswirkungen sprechen, die denen der infolge der thermisch und chemisch bedingten Dichteunterschiede des Magmas stattfindenden insofern ähneln, als dass sie lokal Misch- oder Übergangsformen zwischen elastischen und keplerschen Bedingungen schaffen. Genau das erhellt nachträglich den anfangs als „rein hypothetisch“ empfundenen Untersuchungsgegenstand des variablen Abstands-Exponenten des Kraftgesetzes und seines Einflusses auf die Trajektorien!
Wollte man das genauer untersuchen, bräuchte man einen viel leistungsstärkeren Rechner…
Wenn wir aber nach dem Durchdenken der obigen Zeilen damit zufrieden sind, dass wir nun das gleichzeitige Nebeneinanderbestehen von Balken-Galaxien, offenen Sternhaufen, flachen ellipsoidischen Galaxien mit und ohne synchronisierte Umlaufzeiten nicht mehr als „undenkbar“ innerhalb der bestehenden Gesetzes-Kenntnis erachten, haben wir viel erreicht!
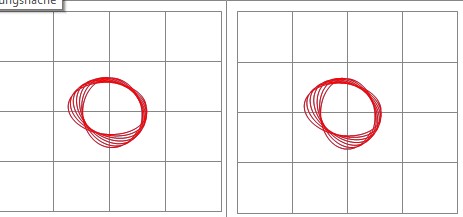
Als Erinnerung hier nochmals eine 3D-Schiel-Ansicht einer Außenbahn (!!) um den „einfachen“ Fall des (flachen) Rotationsellipsoids. (Die Trajektorie muss bei richtiger Augenstellung des „Hinter-die-Bild-Ebene-Schauens“ vor den Koordinaten-Quadraten schweben.)
Jetzt wird es spannend:
A) VOLLKUGEL
Betrachten wir eine kugelsymmetrische Masseverteilung als idealisierte Galaxis mit radiusabhängiger Dichte, so ergeben sich für Innenbahnen (!!) neue Kraftgesetze und also Geschwindigkeitsverteilungen im Idealfall von (immer möglichen!) Kreisbahnen der freien Bestandteile der Masseverteilung (z.B. also Sterne in Galaxien). Wir müssen nur die INNERHALB der Kreisbahn liegenden Kugelschalen betrachten, da im Inneren einer konkreten Kugelschale (trifft auf die ÄUSSEREN Schaken zu) alle Kräfte verschwinden (siehe Integration der Kugelschale unter 2.8.3.1).
Allgemein gilt immer, dass für die Kreisbahn eine Gleichheit von Zentralkraft und Fliehkraft besteht. Da für die Fliehkraft auf dem Kreis immer Ff prop v²/r gilt und mit der Zentralkraft Fz prop r^x gleichgesetzt werden muss, ergibt sich für v die Radius-Abhängigkeit von
v prop Wurzel(r^(x+1))
Spezialfälle sind:
0. verschwindende Dichte gleich Null außer einer zentralen Punktmasse
Die Zentralkraft ist dem Radius umgekehrt quadratisch proportional und ergibt mit
v prop Wurzel(r^(-2+1)) = Wurzel(1/r)
die bekannte fallende Anhängigkeit nach Kepler.
1. konstante Dichte über den Radius (homogene Kugel)
Die Masse der Kugelschalen gleicher Dichte wächst quadratisch mit dem Radius. Jede Kugelschale liefert den gleichen Beitrag zur Gesamtkraft:
Die Zentralkraft ist proportional zum Radius und ergibt mit
v prop Wurzel(r^(1+1)) = r
eine proportional zum Radius steigende Kreisbahngeschwindigkeit, was übrigens einer konstanten Winkelgeschwindigkeit entspricht. (Jede Großkreisebene eines solchen Kugelsternhaufens als Anfangsbedingung bewegte sich also anfänglich idealisiert wie ein starrer Körper!)
2. quadratisch mit dem Radius fallende Dichte
Die Masse aller Kugelschalen ist identisch, da deren Fläche quadratisch mit dem Radius steigt.
Die Zentralkraft ist dem Radius umgekehrt proportional und ergibt mit
v prop Wurzel(r^(-1+1)) = 1
eine konstante Geschwindigkeit (unabhängig vom Radius).
(Es lassen sich nun natürlich auch Übergänge zwischen allen drei Gesetzmäßigkeiten finden.)
Hier ein grafischer Vergleich diverser Dichteverteilungen:
B) KREISSCHEIBE
Betrachten wir nun eine Kreisscheibe als idealisierte Galaxis, haben wir die Kräfte von Kreisringen innen UND außen zu berücksichtigen und aufzusummieren, was schon unter… gezeigt worden ist.
0. Homogene Scheibe mit Radius R
Für die Kraft als Radiusfunktion gilt
r: variabler Abstand vom Zentrum
R: Radius der Scheibe
rr: Integrationsvariable radial
ϕ: Winkel
F(r,R) = -2/(πR²) * ʃʃ (r-rr*cosϕ)/((r-rr*cosϕ)²+(rr*sinϕ)²)^ 3/2 *rr*dϕ*drr [0:π;0:R]
Das Ergebnis ist aus 2.8.3 bekannt:

Die grüne Kurve gilt für die „Längsscheibe“, um die es hier geht.
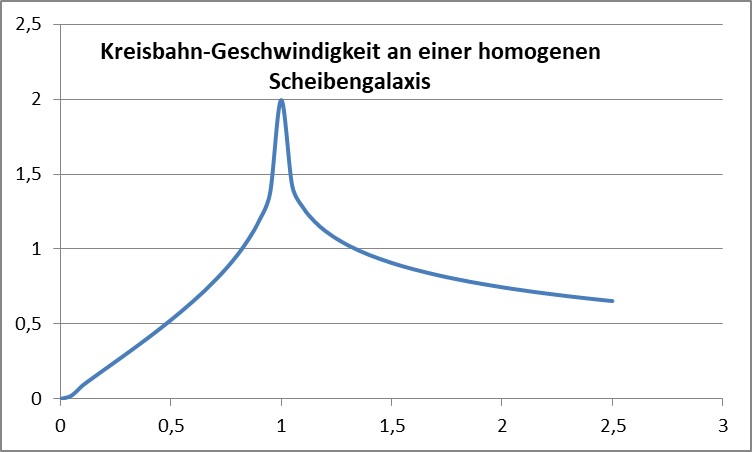
Der Geschwindigkeitsverlauf ergibt sich aus der Wurzel des mit r multiplizierten Kraftverlaufs:
Am höchsten ist also die Geschwindigkeit am Rand der Galaxis, wie die numerische Integration zeigt.
Auch hier sind nun verschiedene Dichtefunktionen der Scheibe denkbar, so dass ganz unterschiedliche Geschwindigkeitsprofile über dem Radius möglich sind.
Der Vergleich zwischen gemessener Verteilung bei einigen Galaxien und berechneter wird bei Wikipedia zum Thema „MOND“ (Modifizierte Newton-Dynamik) so dargestellt:
Hier ein anderes, ähnliches Zitat:

Man erkennt aus den obigen Überlegungen, dass für die Kurve „berechnet“ im Zentrum eine homogene Kugel und dann eine Kreisscheibe und außen ein leerer Raum (mit eine gewissen Übergangszonen dazwischen) angesetzt worden sind.
Es ist klar, dass daraus zwei unterschiedliche Hypothesen folgen können:
- außen etwas stärker als linear mit dem Abstand fallende Scheibendichte (und weil unsichtbar: durch „dunkle Materie“ gefüllt)
- neues Abstandsgesetz der Gravitation (MOND)
Der Vergleich der Rosetten einmal durch relativistische Effekte und zum anderen durch Abweichung von der Kugelsymmetrie lässt aber auch den Schluss zu, dass es lohnen kann, stark exzentrische Rosettenbahnen relativistisch interagieren zu lassen, um zu solchen Geschwindigkeitsverteilungen zu kommen. Hier aber streikt mein kleiner Rechner…
(vgl. auch 2.8.6.3.2, dort etwas ausführlicher an Spezialfällen behandelt!)