Joachim Adolphi

Darstellung von ebenen Richtungen und ihre Umrechnungen in ebenen Polarkoordinaten: Treffer-Auswertung einer Schieß-Scheibe

• Joachim Adolphi
• Sonntag, 19. November 2023
• Sonntag, 26. November 2023
• Abstand, Abstands-Differenz, Drehung einer Kurve, Hyperbel, Polarkoordinaten, Ringezahl, Schieß-Scheibe, Schnittpunkt, Zentralabstand

Schaffen wir es ohne viele Tricks, ebene Richtungen miteinander zu veknüpfen?

Einfache Aufgaben dieser Art beinhalten Abstandsinformationen, aus denen andere Abstände ermittelt werden sollen.

Nebenbei: Es gibt Tiere, die das gut können, indem sie die Informationen aus zwei Sensoren so auswerten, dass sie eine Richtung ermitteln können. Wir gehören dazu: Unsere Ohren vermitteln uns eine Kenntnis über die Richtung, aus der der Schall kommt. Es gibt nur ein winzig kleines Symmetrie-Problem, wenn der Schall aus unserer eigenen Symmetrie-Ebene kommt: Wir können nicht gut unterscheiden, ober von vorn oder hinten kommt, abwohl unsere Ohren meist mehr nach vorne geöffnet sind. Taumelkäfer werten mit Sensoren an den Vorderbeinen die Oberflächenwellen des Wassers aus, die sie beim Schwimmen selber erzeugen, um aus Reflexionen die Beute zu finden, Fledermäuse senden auch eigenen Schall aus und werten die Reflexionen aus.

Könnten wir zum Beispiel mit einigen Sensoren auf einer Ebene den Ursprungsort eines Schall-Ereignisses ermitteln (das ist schwieriger als nur die Richtung allein zu bestimmen: der Abstand kommt hinzu)?

Wir drehen geometrisch das Ganze um:

1. Der geometrische Ort gleichen Abstandes zu einem Punkt ist in der Ebene die Kreislinie (im Dredimensionalen die Kugeloberfläche).

2. Der geometrische Ort einer Abstandsdifferenz zu zwei Punkten ist in der Ebene eine Hyperbel (im Dreidimensionalen ein Hyperboloid), die alle Punkte gleicher Differenz (darstellbar durch zwei Serien konzentrischer Kreise) miteinander verbindet:

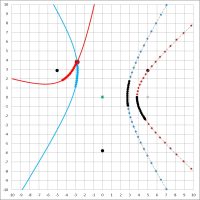
Für die gleichzeitige Auswertung der roten und grünen Kreise ergeben sich für die drei Abstansdifferenzen 0,2 , 0,4 und 0,6 drei Hyperbeln. Diese verbinden in der diskretisierten Darstellung die gegenüberliegenden Ecken der Bogen-Vierecke der Reihe nach, die ihrerseits Schnittpunkte sind von: 4. grüner und 6. roter Kreis, 5. und 7. Kreis, 6. und 8. Kreis usw. usf. oder 3. und 7., 4. und 8., 5,und 9. usw. usf. oder 2. und 8., 3.und 9. usw.usf.. Man kann sich weitere Kreise hinzudenken.

3. Der geometrische Ort zweier Abstandsdifferenzen zu insgesamt drei Punkten in der Ebene ist ein einziger Punkt (oder besser allgemein ein Punktpaar, von dem einer meist unter praktischen Gesichtspunkten ausgeschlossen werden kann), nämlich der Schnittpunkt zweier Hyperbeln. Das ist endlich zufriedenstellend auswertbar!

Wir nehmen eine dritte Kreisschar hinzu:

Nun müsste nur noch eine neue Hyperbeln für das Paar „grün-blau“ eingezeichnet werden. Dazu müssen die Punkte einer Hyperbel 120° um den grünen Mittelpunkt rotiert (oder für rot-blau nach rot verschoben und dort Richtung blau rotiert) werden. Das ist reine Fleißarbeit. Nehmen wir den ersten Fall. Eine Rotation des Punktes (x,y) um den Punkt (xm,ym) um den Winkel w gestaltet sich so, dass

1. der Abstand aus den Koordinaten mit dem Pythagoras bestimmt wird

2. der jetzige Winkel bestimmt wird

3. der neue Winkel bestimmt wird

4. mit dem alten Abstand die Koordinaten mit dem neuen Winkel neu bestimmt werden (unter Berücksichtigung des Bezugspunkte, der ebenfalls neu sein könnte: wir veschieben und drehen also einen Vektor, wenn man so will)

Das ist das Ergebnis für die innere Hyperbel der Abstandsdifferenz 0,6:

Man erkennt zwei wesentliche Dinge:

1. Die beiden Hyperbeln für je 0,6 Abstandsdifferenz schneiden sich in einer Symmetrieachse des Sensoren-Dreiecks, wie es zu erwarten war.

2. Der Schnittpunkt der 0,2-Hyperbel mit der 0,6-Hyperbel liegt außerhalb des Sensor-Dreiecks, aber noch innerhalb dessen Umkreises.

Was wäre ein Grenzfall oder wenigstens ein extremes Ergebnis?

Nun ist der (fast erreichte) Schnittpunkt schon außerhalb des Umkreises des Sensor-Dreiecks.

Wie können wir das entstandene Problem minimieren?

Offenbar ist im echten Messfall der Sensor rechts oben (in diesem angenommenen Fall des fast erreichten Schnittpunkts) als erster von der Schallwelle erreicht. Anschließend wird der links oben erreicht und zum Schluss der untere. Das bedeutet, dass wir die richtigen beiden Laufzeit-Unterschiede benutzt haben, wenn wir davon ausgehen, dass das erste der eintreffenden Signale die Gesamtmessung triggert.

Das bedeutet im Umkehrschluss, dass in solch einem Fall (relativ kleine Differenz und relativ große Differenz) davon ausgegangen werden darf, dass der gesuchte Punkt außerhalb liegt und „nicht in die Wertung“ kommt.

Ein besserer Fall wäre der:

Hier liegen alle drei Schnitte im Umkreis des Sensor-Dreiecks.

Das Ziel der Anordnung ist es, den Abstand der Schallquelle vom Mittelpunkt des Sensor-Dreiecks zu messen und zu kategorisieren, zum Beispiel als Ringezahl einer sensorbestückten Schießscheibe. (Bei alten Mechanik-Scheiben beim Biathlon wird ein Drehimpuls gemessen, der auch Randtreffer bis zu einer bestimmten Stärke berücksichtigen kann, was aber Unterschiede zwischen nah und fern bzgl. des Drehpunktes zur Folge hat…)

Um diese Ziel zu erreichen, müssen wir aus den beiden Zeit-Abstands-Daten den Ursprungsort des Schalls und dann dessen Abstand vom Mittelpunkt errechnen, also erst zwei Hyperbeln gleichsetzen und dann noch den Pythagoras bemühen. Das kann mit einem kleinen Programm abgefangen werden, wenn man erkennt, auf welche Weise die Messdaten in die Hyperbel-Gleichungen eingehen.*)

Ein weiteres Problem muss noch gelöst werden: Ab wann ist ein Schießscheiben-Ring als „angerissen“ zu bewerten? Oder machen wir es mit Zehntelringen? Aber auch dann ist eine Entscheidung zu treffen, wie gerundet wird oder welcher Projektil-Durchmesser zusätzlich zu berücksichtigen wäre. Aber das sind Nebensachen. Hier könte es eine angerissene „8“ sein:

Rein technisch kann man die Sensoren auch weiter nach außen legen bzw. die Schieß-Scheiben-Ringe weiter nach innen. (Maßstab-Frage!)

*) Nun also die Programm-Entwicklung.

Aus dem Spielen mit den EXCEL-Hyperbeln aus den Grundgleichungen und der Drehung um 60° weiß man relativ sicher:

1. Die Schallgeschwindigkeit spielt im Zusammenhang mit dem konstruktiven Sensorabstand eine Rolle, indem sie zusammen für die Zeit stehen, die eine maximale sinnvolle Laufzeitdifferenz darstellt, nämlich den halben Sensorabstand geteilt durch die Schallgeschwindigkeit. Ist die Laufzeitdifferenz größer, muss davon ausgegangen werden, dass die Quelle weit genug außerhalb liegt und somit aus der konkreten Ring-Auswertung fällt: Null Ringe.

2. Die Programmentwicklung kann mit simulierten Schallquell-Orten an statistisch ausgewählten Stellen getestet werden. Dabei werden vorerst logische Fragen zu beantworten sein:

– Wer ist der erste Empfänger (Auswahl des Haupt-Bezugs-Sensors für die Laufzeitdifferenz)?

– Liegt der wirkende Hyperbelast am ersten Empfänger (Brennpunkt-Auswahl für die Hyperbel!) oder gegenüber?

3. Ein iteratives Verfahren für die Schnittpunktermittlung wird wahrscheinlich schneller sein als ein kompliziertes analytisches (muss in der Praxis getestet werden!).

4. Wenn das Programm den Test-Schallquellen-Ort wieder ermittelt, ist es gut.

Fangen wir also mit dem Test-Programm an, das dann teilweise in die „Maschine“ implementiert werden kann:

Vorbereitungs-Schritt: Erstellen eines geeigneten Diagramms für die Darstellung der Sensoren, des Test-„Treffers“ und der ermittelten Treffer-Position sowie der Zwischenergebnisse in Form von Hyperbeln

Schritt 1: Testeingabe eines „Treffers“ und Anzeige im Diagramm über zwei Koordinaten

Schritt 2: Ermitteln der Schall-Laufzeit zu den drei Sensoren

Schritt 3: Auswahl des „nächsten“ Sensors und Ermitteln der Laufzeit-Differenzen zu den anderen beiden

Schritt 4: Formulierung der beiden Hyperbeln in Parameterform und testweise Darstellung im Diagramm

Schritt 5: Iterative Ermittlung des Schnittpunktes der Hyperbeln durch Parametervariation und testweise Darstellung der Iteration im Diagramm

Schritt 6: Ausgabe des Schnittpunktes und Vergleich mit dem eingegebenen Test-„Treffer“

Ausführungs-Ergebnisse:

Schritte 1 is 4 sind relativ direkt in der EXCEL-Tabelle testweise zu realisieren. Dass sie sich im Testtreffer tatsächlich schneiden, ist Beweis ihrer richtigen Parametrisierung, vor allem ihrer richtigen Drehung aus der 1. Hauptlage (hellgrau gestrichelt angedeutet) heraus (was mehrere Fehlerteufel enthalten kann…):

In allen drei Dritteln des möglichen Trefferbereiches (also für jeden der drei möglichen „nächsten“ Sensoren) gibt es eine eindeutige Lösung. Die Fälle direkt auf den Übergangslinien und besonder absolut mittig müssen besonders durch Fallunterscheidung abgefangen werden. Die „online“-Verschiebung des hypothetischen „Treffers“ mittels Schiebereglern ist besonders ästhetisch, wenn sich dann die Hyperbeln biegen und bewegen und schließlich ins andere Drittel umspringen! Die für die Drehung erforderlichen Korrekturwerte der Hyperbeln sind rechts oben tabellarisch zusammengefasst.

Nun geht es also an die Iteration in Schritt 5, da mir die analytische Berechnung zu aufwändig ist. (Einfache Rechnungen sind nur in der ersten Hauptlage machbar, dann aber mit hier nicht zutreffenden variablen Brennpunkten (anders gäbe es auch keine Schnitte!).

Die ersten Ergebnisse sind (wieder nach Beseitigung von schwer zu findenden Leichtsinnsfehlern) vielversprechend und werden in der Genauigkeit noch erhöht werden:

Die schwarzen Punkte auf den roten Hyperbeln dokmentieren die noch grobe Iteration bis zur Abbruchbedingung der Schleife. Die „Treffer“-Vorgabe wird also hier bis auf einen „Zehntel-Ring“ genau erreicht (Ausgabe in den rosa Excel-Zellen). Das wird, wie gesagt, noch intelligenter gestaltet werden.

Damit man alle Abläufe der automatisierten Iteration verfolgen kann, sind noch alle Iterationsschritte sowohl auf den auszuwertenden als auch auf den Hyperbeln in der 1. Hauptlage eingezeichnet (und außerdem die Tabellen-Punkte, aus denen Excel die Hauptlage-Hyperbeln gebildet hat):

Man erkennt an der blauen Kurve, dass sich die Iterationsrichtung umkehren musste, dass aber nicht sofort im ersten Schritt erfolgt ist, weil sich die Punkte trotz falscher Richtung noch angenähert haben. (Das sieht man besobders gut rechts: Start war jedes Mal im Scheitelpunkt.) Es wurden 51 Schritte der Iteration benötigt bis zur eingestellten Genauigkeit. Die Konvergenz des Algorithmus ist also befriedigend.

Die Konvergenz der Iteration ist nicht gut, wenn die Treffer-Punkte aus Sicht eines Nachbarsensors „hinter“ den Sensoren liegen, weil dort die Hyperbeln sehr „spitz“ werden. In der Praxis sollten man also die Sensoren außerhalb des Ringes „1“ anbringen oder eine andere Berechnungsmethode wählen. Hier ein Beispiel, wo auch 500 Iterations-Schritte nicht ausgereicht haben, und ein anderes, wo immerhin fast 400 benötigt worden sind:

 

Farb-Hinweis: In der letzten Version sind die Hyperbeln zwischen den Sensoren unterschiedlich gefärbt, je nachdem, welcher Sensor das erste Signal bekommt und auf Zeit=0 gesetzt wird, fehlt eine der drei Farben: Unten fehlt rot, links grün und rechts blau. Die Scheitel der Hyperbeln zeigen immer zum entsprechenden Nachbar-Sensor (die roten also nach unten z.B. usw. usf.).

Das Iterations-Programm müsste also noch etwas intelligenter mit den Einzelschritten vorgehen. (Ein Versuch, diese Schritte in ihrer Länge vom Abstand zu einem hypothetischen Schnittpunkt der Hyperbeln, nämlich durch ihre Tangenten in den aktuellen Iterations-Punkten ermittelt, abhängig zu gestalten – also analog zum Newton-Verfahren – , bringt neue andere Probleme.)

Anhang:

Was man mit der 3-Kreis-Methode anstelle dieser hier angewendeten 2-Hyperbel-Methode erreichen könnte:

Geht man von der drei Ursprungskreisen aus, deren Radiusdifferenzen aus den Laufzeitdifferenzen unter Berücksichtigung der Schallgeschwindigkeit im Scheibenmaterial folgen, so kann man zu vier Gleicungen mit vier Unbekannten oder drei mit drei gelangen, je nachdem, ob man Winkel oder Koordinaten berechnen will. Das klingt einfach, ist aber in Wirklichkeit komplizierter, weil man beim Auflösen dieser quadratischen Gleichungen auf Probleme beim Ersetzen stößt. Auch die zusätzliche Nutzung von Winkelfunktionen (Kosinussatz!) unter der Randbedingung der Winkelsumme der drei Strahlen vom Trefferpunkt zu den drei Sensoren-Orten sowie deren identischer Abstand untereinander macht die transzendenten Funktionen nicht einfacher.

Implizit bewegt sich jeder Schnittpunkt zweier Kreise konstanter Radius-Differenz eben auf einer Hyperbel. Bei drei Kreisen sind das 6 Schnittpunkte, von denen am Ende der Iteration zwei identisch sein sollen:

Per Hand ist iteriert worden, bis der kleine Kreis so groß geworden ist, dass der große die beiden kleineren genau in einem ihrer eigenen Schnittpunkte schneidet. Das kann man ebenfalls einem Iterationsprogramm übertragen, das dann allerdings die 6 bzw. 5 Schnittpunkte unterscheiden können muss (Dreifachbedingung nach Berechnung aller Schnittpunkte für x und y getrennt, während bei den Hyperbeln nur ein einziger Abstand zu bewerten war).

Die oben angeführte Hyperbel-Lösung erscheint somit als die leichter zum Ergebnis führende.