Joachim Adolphi

2.8.1 Untersuchungen zu nichtstationären Ellipsen bei rotationssymmetrischen Masseverteilungen (Achse senkrecht zur Bahnebene)

• Joachim Adolphi
• Montag, 1. Oktober 2018
• Mittwoch, 19. Mai 2021
• Ellipse, Ellipsenbahn, Galaxie, Keplersche Gesetze, Kreisbahn, Massering, Massescheibe, Präzession, Rosette, stationär

Wir alle kennen aus der Schule die Keplerschen Gesetze. Sie behandeln die Form der Planetenbahnen und die hinter ihnen stehenden Zusammenhänge zwischen Ellipsenhalbachsen, Ellipsenbrennpunkt oder numerischer Exzentrizität, Umlaufzeit und Geschwindigkeit. Der Kreis als Sonderform der Ellipse ist dabei natürlich auch immer enthalten. Man nimmt einfach zur Kenntnis, dass es sich dabei um im Raum stabile, also stationäre Ellipsen handelt, ohne diese Besonderheit genauer zu hinterfragen. Man nimmt auch zur Kenntnis, dass man bei der Anwendung des Gravitationsgesetzes einfach die jeweiligen Gesamtmassen der Objekte in ihren Schwerpunkt legt und somit bei kugeligen Körpern einfach mit dem Mittelpunktabstand rechnet.

Dass das im Falle von Kugeln (aber nur von Kugeln!) erlaubt ist, wurde im Abschnitt „Numerische Integration“ im Beispiel 4 nachgerechnet.

Hier die Kugel-Volumen-Doppelschleife der Integration über den Winkel (Kreisringe einer Kugelschale) und den Radius (Kugelschalen) und die Kraft-Doppelschleife über die Achskomponente der 3D-Kraft:

„korr“ ist 0,5, um für die Fehlerminimierung in erster Näherung die Querschnittsmitte der Ringe zur Integration zu nehmen. Die Werte für Kräfte und Volumina stimmen mit den analytischen bei 600 x 600 Schritten gut überein (alle Konstanten 1, Probemasse direkt auf Oberfläche).

(Hinweis zur Wahl der Integrations-Prozedur: Man kann natürlich in kartesischen Koordinaten genauso gut wie in Polarkoordinaten arbeiten. Bei genügend feiner Schachtelung wird der Fehler hinreichend klein. In kartesischen Koordinaten macht man bei konstanten Volumenelementen eine eine Zusatz-Abfrage, ob man innerhalb der analytisch angegebenen Oberfläche liegt. In Polarkoordinaten entfällt diese Abfrage, dafür ist das Volumenelement koordinatenabhängig.)

Die Folgen des Auseinanderlaufens von Masse-Schwerpunkt und Gravitations-Schwerpunkt bei zwar rotationssymmetrischen, aber nicht kugelförmigen Masseverteilungen erlebt man am besten bei einer Modellrechnung von Flugbahnen, auch „Trajektorien“ genannt.

Einige Vorbetrachtungen sollen den Blick dafür schärfen:

– Ist die Masseverteilung rotationssymmetrisch (Achse senkrecht zur Bahnebene!), so sollte bei einer „richtig“ eingestellten Umlaufgeschwindigkeit auch eine rotationssymmetrische Bahn möglich sein (und das wäre ein Kreis, der per se stationär ist), weil die Kraft immer entlang der Symmetrieachse der Anordnung wirkt und diese den Mittelpunkt der Anordnung enthält, auch dann, wenn das momentane Schwerkraftzentrum (ein hypothetischer Schwerkraftmittelpunkt, ermittelt aus Gesamtmasse in Punktform und integrierter Kraftwirkung der tatsächlichen Masseverteilung) nicht im Symmetriezentrum, aber natürlich auf der Verbindungslinie von momentanem Bahnpunkt und Masseschwerpunkt liegt. (Siehe oben angeführtes Beispiel 4!)

– Bei einer „nicht richtig“ eingestellten Umlaufgeschwindigkeit sollte die Kraft-Integration über die Massenverteilung und die doppelte Zeitintegration über die sich daraus ergebenden Beschleunigungen („Geschwindigkeitsänderungen“) dann die Trajektorien ergeben, die ganz allgemein nichtstationäre Ellipsenform haben sollten, mit anderen Worten Rosetten bilden müssten (diese wären die Überlagerung von einer Ellipse um ein kreisförmig – oder ebenfalls ellipsenförmig?? – wanderndes Schwerezentrum).

– Für die Prüfung der Plausibilität der Ergebnisse muss die Schrittweite der numerischen Integration variabel sein können, um Artefakte ausschließen zu können.

– Für das Spielen mit der 3D-Physik in einer 2D-Bahn-Symmetrie-Anordnung sollten Masseverteilung, Startort und Startgeschwindigkeit variabel einstellbar sein. Für ganz Neugierige könnte man noch den Exponenten des Abstandes im Gravitationsgesetz variieren (erledigt: siehe 2.8.3.2).

Nun müssen nur noch die Startwerte und alle Parameter eingegeben und vernünftig miteinander verarbeitet werden:

Vorversuch: Geometrie-unabhängiger Test des Einflusses des Abstands-Exponenten bei einer PUNKTMASSE

Die Gravitation wird wie jedes „konservative Potential“ so verstanden, das sich die Wirkung im Raum nicht schwächen soll, also ein geschlossenes Oberflächenintegral unabhängig von der Art der Oberfläche den Wert der eingeschlossenen Quelle wiederspiegelt und dass vor allem längs einer geschlossene Bahn (reibungsfrei!) keine Arbeit verrichtet wird. Macht man es sich leicht, wählt man als Oberfläche konzentrische Kugeln um die Quelle. Da deren Oberfläche mit dem Quadrat des Radius wächst, muss die Quell-Wirkung mit dem Quadrat des Radius sinken – und fertig ist der Lack. Und die Bahnen? Die wählt man nicht, sondern lässt sie Schritt für Schritt durch numerische Integration entstehen!

Sehr komplizierte analytische Rechnungen (im Abschnitt 2.8.3 ausführlicher, besonders in 2.8.3.2) führen dazu, dass die Bahnen von nur mit der Quelle wechselwirkenden (sonst also kräftefreien) Objekten ortsfeste Ellipsen (darunter als Spezialfall der Kreis) mit der Quelle im Brennpunkt sein müssen.

Das testen wir mit unserem numerischen Modell gleich aus, indem wir die Quelle zum Punkt schrumpfen lassen und den Exponenten (unter jedem Bild angegeben!) variieren (ausführlicher ist das dort dargestellt):

FAZIT: Stärkerer Abfall der Kraft macht größere Ellipsen mit Apsidendrehung (manchmal – auch bei mir! –  fälschlich als „Präzession“ bezeichnet), schwächerer Abfall kleinere

Erster „richtiger“ Versuch: Einfachster Fall einer RINGMASSE

Man sieht, dass als einfachster Fall eine kreisförmig angeordnete Anzahl von Punktmassen die „Scheibe“ der Masseverteilung annähernd genau darstellen soll, was durch die Prüfung mit der Änderung der Zeitschritt-Konstanten bei der Integration bestätigt werden kann. Erst bei sehr großer Annäherung der Flugbahn an die Punktmassen und großen Zeitschritten ergeben sich solche hübschen Artefakte, bei denen natürlich auch der Energiesatz flöten geht, weil viel länger (nämlich einen ganzen Zeittakt lang), als es bei genauerer Rechnung erlaubt wäre, große Kräfte walten können:

Nun aber zur systematischen Auswertung:

– Kreisbahnen sind möglich (und natürlich stabil), wenn man die richtige Startgeschwindigkeit wählt (Radialkraft gleich aktueller Schwerkraft):

Findet man die „richtige“ Startgeschwindigkeit nicht, so ergeben sich andere Formen:

Es kann aber gelingen, auch andere „stationäre“ Bahnen zu finden, wo das Wandern der Ellipsen-Achse („Drehung der Apsidenlinie“) ein rationales Verhältnis mit der Geschwindigkeit eingeht:

Hier die „echten“ mathematischen (nicht modellierten, sondern gerechneten!!) Zyklozykloiden:

Und hier die „reziproken“ Werte, die aus der Technik geläufiger sind (Planetengetriebe, absoluter Bahnpunkt eines Planetenradrandpunktes bei rotierendem Sonnenrad):

Noch verrückter wird es bei einem Umlaufgetriebe, das ich einmal für meine Studenten visualisiert habe (Videostills der gleichen Grundeinstellung):

– Die Ellipsen können also grundsätzlich gar nicht stationär sein und bilden deshalb Rosetten, die bei glücklich gewählten Parametern ihrerseits aber an „stationäre Rosetten“ beliebig weit angenähert werden können und auch „dicht daneben“ spannende Muster bilden:

(Das Verhältnis der Apsidendrehungs-Frequenz zur Umlauffrequenz erinnert an die Berechnung in Planetengetrieben, wo die Eigendrehung des Käfigs oder des Sonnenrads ebenfalls mit berücksichtigt werden muss.)

Es stellt sich nun die Frage: Können beide Formen (Bahn-Rosetten und mathematische Zyklozykloiden) wirklich identisch sein, wenn das Geschwindigkeitsgesetz unterschiedlich aufgebaut ist: Bei der Zyklozykloide durch rein geometrische Überlagerung, bei der Rosette aber energetisch? (Vielleicht kommt die Antwort bei weiteren Untersuchungen? siehe 2.8.3.2!)

Erstes FAZIT:

Weicht man in der Masseverteilung des „Zentralgestirns“ von der homogenen Kugel in Richtung eines flachen Rotationsellipsoids ab, so hat man es mit einer mitrotierenden Abstandsabweichung des Gravitationszentrums vom Massezentrum zu tun, die tatsächlich (ohne die analytische Lösung des Problems zu kennen!) eine Superposition zweier Rotationen zur Zyklozykloide verursacht.

Zweiter Versuch: Nächst einfacher Fall einer SCHEIBENMASSE

Auch hier sind Kreisbahnen und stabile Zyklozykloiden einstellbar. Die „Chaosfälle“ sind natürlich noch chaotischer, weil jetzt die Scheibe als Schar konzentrischer Ringe aus Einzelmassen geformt ist.

Die VBA-Integration der aktuellen Kraftkomponenten läuft jetzt natürlich über eine Doppelschleife, wobei der Einfachheit halber die Koordinaten und Massen des äußeren Rings radiusproportional nach innen verringert werden.

Die grafische Darstellung über eine konzentrische Kreisschar zeigt anschaulicher, dass die eigentlich verwendeten Punktmassen radiusproportional sind, was in der Punktdarstellung leider nicht klar erscheinen kann. Dafür ist die Möglichkeit des „Durchwanderns“ wie bei einem Sternhaufen aber klarer ersichtlich!

Zweites FAZIT:

Wie schon erwartet, unterscheidet sich die Scheibe qualitativ nicht vom Ring. Die Parameter sind natürlich anders einzustellen, um die gleichen geometrischen Effekte zu erreichen. Bei gleicher Gesamtmasse ist die Scheibe der Punktmasse ähnlicher als der Ring, was sich – in anderem Zusammenhang, z.B. bei der Getriebe-Berechnung – auch in ihrem geringeren Trägheitsmoment zeigt.

Dritter Versuch: Flacher Rotationsellipsoid (Diskus) und stabförmiger (Speer) im Vergleich mit der Punktmasse (Kugel)

Die Berechnung des Schwerefeldes des Rotationsellipsoids und seine Auswirkung auf die Flugbahn erweist sich als deutlich schwieriger, weil man jetzt tatsächlich dreidimensional rechnen muss. Die dreifache Integration erfordert ein angepasstes Volumenelement mit den entsprechend faktorbehafteten partiellen Differentialen.

Parameterdarstellung des z-Rotations-Ellipsoids:

x = r*sinΘ*cosϕ

y = r*sinΘ*sinϕ

z = a*r*cosΘ

3 x 3 – Matrix der partiellen Ableitungen d(x,y,z)/d(r,Θ,ϕ):

Partielle Ableitungen

Koord   d/dr                                      d/dΘ                                    d/dϕ

x             sinΘ*cosϕ                          r*cosΘ*cosϕ                    – r*sinΘ*sinϕ

y             sinΘ*sinϕ                           r*cosΘ*sinϕ                     r*sinΘ*cosϕ

z              a*cosΘ                                -a*r*sinΘ                           0

Die Determinante ergibt den Faktor für die numerische Volumen-Integration:

sinΘ*cosϕ*r*cosΘ*sinϕ*0 + r*cosΘ*cosϕ* r*sinΘ*cosϕ* a*cosΘ +

+ (- r*sinΘ*sinϕ)* sinΘ*sinϕ*(-a*r*sinΘ) – sinΘ*cosϕ*r*sinΘ*cosϕ*(-a*r*sinΘ) –

– r*cosΘ*cosϕ* sinΘ*sinϕ*0 – (-r*sinΘ*sinϕ)* r*cosΘ*sinϕ* a*cosΘ

2 Summanden sind 0, die anderen 4 ausgeklammert und zusammengefasst lauten

= ar²*(cos²Θ*sinΘ*cos²ϕ + sin³Θsin²ϕ + cos²Θ*sinΘ*sin²ϕ + sin³Θ*cos²ϕ)

2 Pärchen (1+3 und 2+4) enthalten ausgeklammert je den Faktor sin²+cos²=1, woraus als Rest bleibt:

= ar²*( sin³Θ + cos²Θ*sinΘ)

dV = a*r²*(sin³Θ + cos²Θ*sinΘ)*dr*dϕ*dΘ

Das ergibt dann folgenden Hauptteil des Codes und ein schon recht komplexes Bild in EXCEL:

Die Proberechnung über eine Dreifachschleife für das Volumen des Ellipsoids ergibt im Vergleich zur analytischen Formel

V = 4/3*pi*a*r³

schon bei nur 20x20x20 Elementen für a=0,5 und einem an ein festgelegtes Standardvolumen (Kugel r=1) angepassten r_xy= 1,26 und r_z = 0,63 eine erstaunliche Übereinstimmung im Volumen (und bestätigt die obige Rechnerei des Differentials!) und für eine Probemasse im Abstand 2r von der Achse eine merkliche Vergrößerung der Kraft im Vergleich mit einer Kugel gleichen Volumens:

V anal. Ell. u. Kugel	4,18879
V VBA Ellipsoid	4,18405
F VBA Ellipsoid	1,15463
F anal. Kugel	1,04720

Nun kann man also wieder zur Bahnberechnung übergehen, indem man den Volumenelementen die Kraftelement-Komponenten zuordnet und durch zweifache Zeitintegration die Bahnen für zwei identische Objekte mit gleichen Startwerten um zwei massegleiche Ellipsoide (nur zu Vergleichszwecken grafisch übereinandergelegt, nicht tatsächlich koexistent im gleichen Raum!!) sukzessive erhält:

Die inneren roten und blauen Kreise symbolisieren die Äquators der flachen (blau) und schlanken (rot) Rotationsellipsoide gleichen Volumens, aber reziproker Abplattung. Im Falle der Kugel (beide identisch) ergibt sich die erwartete stationäre Ellipse (bis auf winzige numerische Artefakte).

Man sieht sehr deutlich, dass die Apsidendrehung umso stärker ist, je größer die sich in z-Richtung aufhebenden Kraftanteile sind, was naturgemäß für stark exzentrische Ellipsen ausgeprägter ist.

Der Sonderfall der Kugel als Zentralobjekt (grün) ist ein guter Vergleich. Vor allem aber: Man erkennt bei genauer Bahnverfolgung, dass die Abweichung von der „ordentlichen“ stationären Ellipse im Nahbereich passiert, weil dort die Wirkung der z-Komponenten der Kraft am größten ist und sich damit der größere Anteil aufhebt und die Bahn nicht gekrümmt genug ist, um wieder in die „alte“ Ellipse gelangen zu können, was zu einer Apsidendrehung gegen die Drehrichtung führt. Die entfernte Krümmung um den entfernten „Brennpunkt“ sieht gut aus und erinnert stark an die „echten“ Ellipsen um eine Punktmasse. Mit anderen Worten: Die Verbindungen vom Ursprung zu den beiden „Brennpunkten“ sind NICHT parallel, sondern bilden einen Winkel (halber Apsidendrehungswinkel pro Umlauf), der umso größer wird, je näher man sich an den „Speer“ annähert! Für den „Diskus“ gilt entsprechend umgekehrt, dass die Kraft nahe am Zentralgestirn größer als bei der Kugel gleicher Masse ist und deshalb die Ablenkung „vorwärts“ zu stark wird und eine Apsidendrehung in Drehrichtung erfolgt.

HINWEIS:

Für die hier beschriebene ebene Apsidendrehung ist NICHT die Bahnneigung gegen den Äquator ursächlich, wie das bei der ISS-Rechnung nachgewiesen worden ist (dort war das auch über die Kreiselgesetze zu bestimmen). Eine Umformulierung des Gravitationsgesetzes in Anlehnung an Punktmassen müsste mit einem variablen Abstandgesetz (Exponent) oder mit einem wandernden „Schwerkraftzentrum“ arbeiten, das bei einer Scheibe in Richtung der Probemasse und bei einem Stab in Gegenrichtung (abstandabhängig!) verschoben ist. Es wirkt dann, als ob eine mitbewegte Zugvorrichtung die Bahn beeinflusst.

(Hierzu sollten zusätzlich Energiebetrachtungen angestellt werden, um aus den Kräften die Ableitung des Potentials und daraus das Potential bestimmen zu können und über den Energiesatz – potentielle und kinetische – die Probe machen zu können!)

Der Rest ist stundenlanges „Spielen“, das heißt Werte einzustellen und zu vermuten, was passieren müsste, und dann eben zu gucken, was wirklich „passiert“, ob eben die „Vorurteile“ richtig waren…

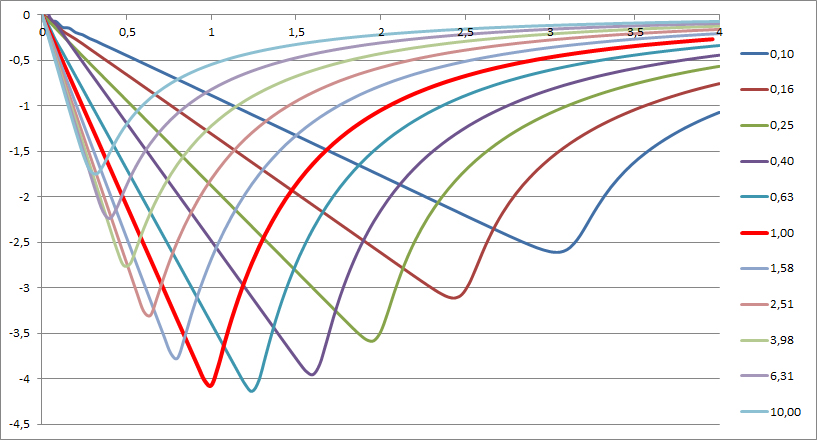
Zur „abschließenden“ (!?) Verfeinerung kann man natürlich nun auch noch die Kraftfelder mit dem Parameter der Abplattung (Radius-Faktor kleiner als 1) des Ellipsoids aufnehmen und als Kurvenschar darstellen. Das Prinzip ist durch die bisherigen Versuche klar geworden, aber der Genießer möchte auch noch in der geschickt dargestellten Grafik schwelgen:

Die dicke rote Kurve ist die Kugel mit dem z/xy-Verhältnis 1,0 und die dunkelblaue der Diskus 0,1 und die hellblaue der Speer 10,0. Die Hyperbeln des äußeren Kraft-Verlaufs haben sowohl für die Disken wie für die Speere einen deutlich erkennbaren Abszissen-„Offset“, denn sie erscheinen abszissenparallelverschoben statt x-y-symmetrisch. Dieser Offset zeigt genau die Verschiebung des Gravitations-Mittelpunkts gegen den Schwerpunkt (in/gegen die Richtung der sich bewegenden Trajektorien-Probemasse!) an. Das war durch die (daraus folgende!) unterschiedlichen Apsidendrehungsrichtungen der Bahnen nicht anders zu erwarten!

(Die Schwankungen um den Ursprung sind numerische Artefakte.)

FAZIT:

Unsere Experimente haben gezeigt, dass aus der STRUKTUR der Bahnen auf ihr WERDEN geschlossen werden kann (hier vielleicht besser: aus der Wirkung auf die Ursache?), ganz im Sinne des Titels dieser Website.

Dass zwischendurch verschiedene Fehler bei der Modellierung passiert sind, ist sonnenklar:

• Verwechslung von Winkeln bei der Übertragung der Determinante in die Programmiersprache
• Falsche Reihenfolge der Berechnung und Ausgabe (wirre Hysteresen statt numerisch bedingt flache)
• unkluge Zellaufteilung der Volumina, deshalb größere numerische Fehler

Das passiert auch erfahrenen Programmierern, weil sie gerade im Bewusstsein ihrer Erfahrung zu schnell und also zu wenig gründlich denken und arbeiten (Abkürzungen werden dann zu Umwegen!).

Natürlich kann man das auch echt zeitabhängig in VB programmieren und die bewegten Körper mit „Spuren“ versehen, damit man die Trajektorien sehen kann. Sind die „Tapsen“ in konstanten Zeit-Takten erfolgt, sieht man an ihrer Dichte auch nachträglich die Geschwindigkeit.

Hier zwei Bilder, die die Ähnlichkeit der Wirkungen von Abplattungs- oder Kraft-Gesetz-Exponenten-Änderung für ebene Bahnen um Rotations-Ellispoide zeigen sollen (ausführlicher unter 2.8.1.0 dargelegt!):

In beiden Fällen ergibt sich eine „Vorwärts-Apsidendrehung“ der gedachten Ellipse (in allen Darstellungen linksdrehend, Planet waagerecht rechts beginnend), die im rotierenden System eigentlich nur eine Schwingung um einen Gleichgewichts-Abstand darstellt, wobei NUR bei der Kepler-Ellipse Schwingzeit und Umlaufzeit identisch sind.

Übrigens sind diese Apsidendrehungen auch bei vergleichbar großen Massen von Doppelsternen zu sehen:

Das Spiel mit diesem Programm ist spannend, weil viele Parameter geändert werden können. Man lernt ganz nebenbei die „zufälligen“ Besonderheiten der Keplerschen Gesetze schätzen! (Beim scharfen Hinsehen erkennt man auch, dass das Programm ständig erweitert wird…)

Nun hat man Lust auf Vertiefung: Im nächsten Abschnitt soll nun auch die dritte Dimension genutzt werden, um die Kugel-Symmetrie weiter aufzuheben. Dann werden also einerseits dreiachsige Ellipsoide betrachtet werden und andererseits die Bahnen aus der x-y-Ebene herausgeführt.

(Genauere Vergleiche sind in 2.8.1.0 dargelegt.)