2.4.3.8 Rekristallisation
Kann man Rekristallisation verstehen und zur Probe auf makroskopische Objekte übertragen?
Was ist eigentlich unter „Rekristallisation“ zu verstehen?
Im engeren Sinne meint man damit, dass in einem relativ ungeordneten Festkörper kristalline Bereiche entstehen, die makroskopisch (mit bloßem Auge) zu sehen sind. Wenn sich zum Beispiel nach einem festen Phasenübergang, der die alte Kristallstruktur zerstört hat, weil die neue Phase einem anderen Kristallsystem angehört, neue kristalline Gebiete bilden, so ist das auch „Rekristallisation“, obwohl das „Re-“ hier nicht ganz zutrifft, denn es sind ja andere Kristalle.
Wenn sich neue Kalzit-Kristalle in den Kalkschalen von Fossilien bilden, so gehört das auch dazu.
Im weiteren Sinne kann man jede Umgruppierung von räumlich gleichen oder ähnlichen Elementen, die zu einer höheren Ordnung führt, „Rekristallisation“ nennen.
Und in einem noch anderen Sinne kann man auch das Umkristallisieren „Re“-Kristallisieren nennen, denn nach der Auflösung oder Aufschmelzung wird der gleiche Stoff wieder ksistallisiert (wichtiges Reinigungs-Verfahren z.B. für Zucker aus der Lösung oder Halbleiter-Werkstoffe aus der Schmelze).
Fangen wir also mit identischen Elementen an.
1. Umgruppierung von Kugellager-Kugeln
Füllen wir ein Volumen (zum Beispiel eine zylindrische Creme-Dose) mit solchen Kugeln, liegen sie relativ ungeordnet darin:
Man erkennt, dass der einhüllende Rand des Volumens (die Innenwand der Schachtel) einen relativ großen Einfluss auf die anliegenden Kugeln hat, diese sich dem Rand also anpassen. Untereinander aber sind sie relativ ungeordnet, obwohl sich die meisten berühren. Die Nahordnung, dass jede Kugel in ihrer 3D-Umgebung bis zu 12 Kugeln berührt, ist fast gegeben, von einer Fernordnung aber kann man nicht sprechen, da schon die übernächste Kugel keinerlei geordnete Beziehung mehr eingegangen ist.
Führen wir eine „passende“ Menge Energie pro Kugel hinzu, zum Beispiel durch leichtes Schütteln oder hartes Aufsetzen der Schachtel, so reicht diese Energie dazu aus, dass Umordnungs-Prozesse stattfinden. Deren „Richtung“ geht statistisch zu einer geringeren potentiellen Energie jedes Teilchens, also auch der Gesamtheit, hier also „nach unten“, entsprechend der Richtung der Schwerkraft. So weit es die äußere Begrenzung des Volumens zulässt, wird also eine „dichteste Kugelpackung“ enstehen, ein kubisch-raumzentriertes Gitter, das aus der Blickrichtung parallel zur Schwerkraft wie „Kugelreihen auf Lücke“, also hexagonal (Schichtfolge ABC), aussieht.
Jetzt kann man gut erkennen, dass eine Schicht komplett geordnet ist, während sowohl der Rand als auch die „Rest-Kugeln“ der darüber angefangenen Schicht nur teilweise ordnung aufweisen. Die Nahordnung und die Fernordnung gehorchen dem gleichen Translations-Gesetz, die Kugeln bilden ein 3D-Gitter wie ein kubisch flächenzentrierter Kristall, wo jede Kugel exakt 12 3D-Nachbarn oder exakt 6 2D-Nachbarn hat.
Wir haben eine ideale „Rekristallisation“ erlebt und können das Experiment durch grobes Schütteln und anschließendes mehrfaches hartes Aufsetzen der Schachtel beliebig oft wiederholen.
2. Rekristallisation von Schwerspat (Baryt)
Im Osterzgebirge gibt es an verschiedenen Stellen rhythmisch abgesetztes Bariumsulfat mit Eisenoxid-Beimengungen, den sogenannten Lagenbaryt, der in rosaroten Streifen ein dekoratives Gestein abgibt, das optisch dem Achat ähnelt. Im Anschliff erkennt man an den Reflexen, dass etwa senkrecht zur Schichtebene einkristalline Gebiete entstanden sind, die nur durch Rekristallisation oder Umkristallisation zu erklären sind. (Das Umkristallisieren wird in der chemischen und Lebensmittel-Industrie auch als Reinigungs-Verfahren eingesetzt, zum Beispiel beim Zucker.)
Es ist manchmal schwer zu entscheiden, ob zonierte Kristalle oder rekristallisierte Schichten von mIkrokristallen vorliegen, wie dieses Beispiel von Amethyst aus Cunnersdorf zeigt, bei dem es sich eindeutig um fein zonierte große Kristalle handelt:
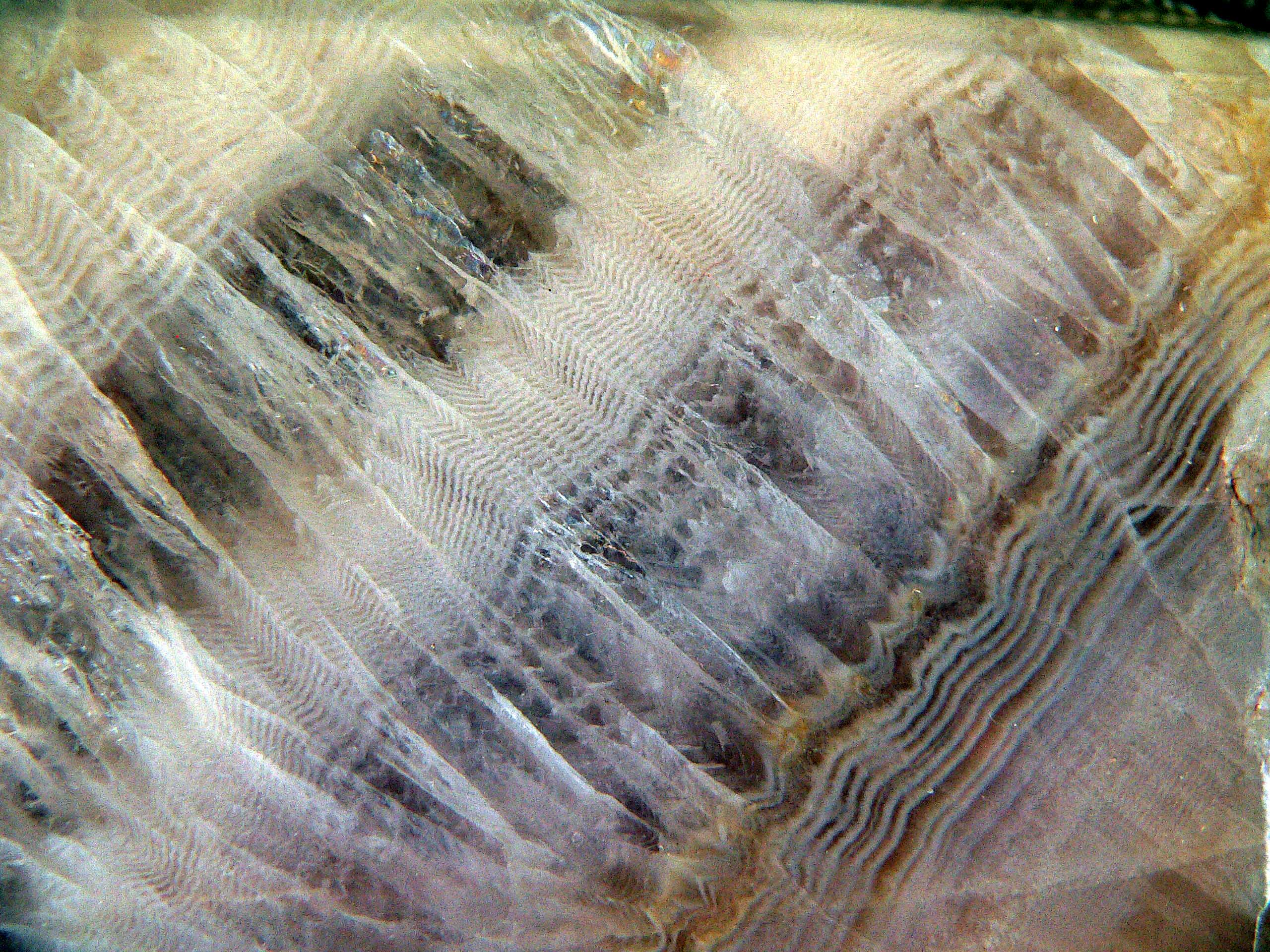
Ausschnitt aus einem Cunnersdorf-Amethyst: die senkrecht zur Schichtung verlaufenden hellen Reflex-Linien sind Korngrenzen der großen Kristalle
3. Rekristallisation von Kalkspat (Kalzit) in Fossilien
In vielen Schalentieren bilden sich sogar Einkristalle aus Kalzit. Wenn man Glück hat, findet man in der Rügener Kreide (oder auf Moen) frisch aus der anstehenden Kreide gebrochene Fossilien, deren Kalkschale noch erhalten ist. Wenn man noch mehr Glück hat, sind darin rekristalliserte Gebiete enthalten.
Nutzt man die Tatsache, dass frisch gebrochene Kalzit-Kristalle einen guten Glanz haben, so kann man über weite Strecken des Stücks gleiche Glanzwinkel feststellen:
Die weißlich glänzenden Gebiete haben den gleichen Glanzwinkel.
4. Umordnung von flächigen Elementen: Blätter im Wasser
Die am grasigen Ufer vom Wellenschlag gestapelten Blätter (Stechlin, Mecklenburg-Brandenburgische Seenplatte) werden immer wieder leicht angehoben und können sich mit der Zeit die „beste“ Position aussuchen. Hört der Wellenschlag auf, bleibt die Ordnung erhalten, wird er stärker, beginnt eine neue Umordnung.
Einzelne Stapel kann man im strömenden Wasser eines Baches finden, wenn die Blätter auf ein Hindernis stoßen, z.B. einen Stein oder einen Stock oder einen ins Wasser hängenden Zweig. Dieser Stapel erreicht eine kritische Maximalhöhe, bevor er seitlich ausweicht und also zerbricht. Dann baut er sich wieder neu auf usw. usf.
In diesem dynamischen System kann man also eine Korrelation von Stapelbreite und Stapelhöhe erkennen, die von den Kontakteigenschaften seiner Elemente abhängt. Der rhythmische Zeitablauf des Geschehens wird um so „sauberer“, je konstanter alle Parameter „eingestellt“ sind.
5. Umordnung von linienförmigen Elementen: Stängel im Wasser
Bei „eindimensionalen“ Objekten wie Halmen oder Stängeln (hier: vorjährige Schilf-Stängel am Ufer des Roofensees in Brandenburg) wird diese Korrelation von Element-Abmessung und Stapel-Abmessung noch deutlicher und erinnert an die Zusammenhänge zwischen den Struktur-Parametern von „Riffeln“:
Man kann deutlich erkennen, dass die rein parallele Ausrichtung zum Ufer gebrochen wird, wenn die Wellen in eine „Ecke“ laufen, die zum Beispiel durch einen umgestürzten Baum gebildet werden kann. Dann ergeben sich ebnfalls durch den ständigen Wellenschlag Nahordnungsbereiche, die natürlich parallel aussehen, die aber ungefähr bei einem Stapelhöhe-Stapelbreite-Verhältnis von 1 liegen, sogar dann, wenn die Stapelbreite aus ungleich langen Halm-Stücken teilweise zusammengesetzt wird.
Ist der Winkel zwischen Stamm und Ufer sehr klein, können sogar „Fächer“ von Halmen entstehen, die ihrerseits etwa gleich große Flächen beanspruchen, deren Durchmesser etwa in der Elementelänge liegt.
Ist der Wellenschlag zu stark oder der Seitendruck (Wind) zu hoch, so wird die Monolage, die Voraussetzung für die zweidimensionale Strukturbildung ist, gestört, und es entsteht meist ein etwas chaotischer Stapel in der dritten Dimension, weil das Abtauchen der unteren Schicht zu neuen wirkenden Kräften führt, die nur wenig mit denen der Wellenbewegung korrelieren können.
6. Chemisches und strukturelles Umordnen von Mineralien in Gesteinen
Das ist ein weites Feld… (siehe auch: 2.7.2.3)
Schön sieht man das Ganze aber an den Feldspäten in Graniten und Porphyren, wenn sie zonierte Gebilde werden oder verzwillingt sind. Mineralien, die unter sehr hohem Druck und unter hohen Temperaturen in Tiefengesteinen gebildet wurden und dort stabil sind, zersetzen sich sehr langsam, wenn Druck und/oder Temperatur als Folge der Abtragung des darüber liegenden Deckgebirges niedriger werden.
Im OEG ist es häufig an farblichen Ummantelungen der Feldspäte zu sehen, bei nordischen Geschieben an zusätzlichen schwarzen Streifen innerhalb der Feldspatkristalle durch rhythmische Ausscheidung von Metalloxiden:
















Kommentar abgeben