Pi: Universelle Naturkonstante aus der Schwingungsgleichung für Anfänger
(Letzte Änderung: 12.02.2020)
Jeder lernt in der Schule die „Kreiszahl Pi“ kennen. Gute Mathelehrer lassen sogar Regentropfen (statistische Verteilung in der Ebene) auf ein Quadrat und einen Kreis fallen und lassen durch Zählen der Tropfen das Flächen-Verhältnis und somit Pi bestimmen. (Man könnte auch die Kästchen des Karopapiers zählen…) Oder eine Nadel wird möglichst oft auf parallele Linien fallengelassen und die mittlere Zahl der Schnittpunkte mit den Linien ermittelt usw. usf.
Das alles wirkt aber auf einen naturphilosophisch interessierten Schüler „gewollt“.
Gibt es einen Ausweg? Ja, den gibt es, aber er ist für Schüler jenen Alters, in dem sie gerade erst Kreise berechnen können sollen, leider noch zu kompliziert.
Normalerweise lernt man später erst die Sinusfunktion kennen, dann die Schwingungsgleichung und dann die Sinusfunktion/Kosinusfunktion als Lösung der Schwingungsgleichung. Das reicht für den Lerntyp unter den Menschen aus, weil die Kenntnis von Pi dabei vorausgesetzt wird.
Hier soll die Schwingung als die logische Wirkung einer Ursache behandelt werden, ohne dass man die Sinusfunktion oder die Kreiszahl Pi kennt. Ob das gelingt??
Philosophischer Grundsatz ist spätenstens seit den „alten Griechen“: In der Natur geht es „verhältnismäßig“ zu, das oberste Gesetz ist das der Proportion.
In welcher „Qualität“ oder Proportion ist nun Pi versteckt?
Eine besondere natürliche „Qualität“ ist die „Stabilität“ eines Zustands, worunter man versteht, dass dieser Zustand auf Änderungen mit einer rücktreibenden Wirkung reagiert: Je stärker die Abweichung vom „stabilen Zustand“, desto größer die „rücktreibende“ Wirkung.
Einfachstes physikalisches Beispiel: Mechanische Schwingung.
(Komplizierteste gegenwärtige Fragestellung: Klima!)
Einzige logische Voraussetzung ist der Sachverhalt, dass eine rücktreibende Kraft vorhanden sei, deren Größe proportional zur geometrischen Abweichung einer Masse aus der Ausgangslage ist. Setzen wir im Gedankenexperiment mit einer trägen Masse und einer (linear elastischen) Feder alle physikalischen Größen dimensionslos auf Eins, bleibt eine mathematische Gleichung übrig, in der die zweite Ableitung der Orts-Zeit-Funktion der Masse, also x“(t), dem Ort der Masse, also x(t), negativ (weil „rück“-treibend) proportional ist:
F(x(t)) = -k*x(t) = m*a(t) = m*x“(t)
x“(t) = -x(t) mit k=1 und mit m=1
Gehen wir nun von dem Theorem aus, dass jede stetige Funktion (und durch solche sollten makroskopische physikalische Vorgänge beschreibbar sein) durch eine Überlagerung („Reihenentwicklung“) von Potenzfunktionen (Taylor-Reihe) darstellbar ist, wenn man bei deren Summation die Faktoren richtig wählt, so brauchen wir nur noch die Potenzregel des Differenzierens, um die Lösung für obige Gleichung zu finden. Diese Potenzregel lautet (wie durch einfache Zahlenbeispiele überprüfbar ist), dass beim Differenzieren einer Potenz der Exponent um Eins sinkt und als Faktor vor der verminderten Potenz erscheint.
Macht man das zweimal, wie die obige Gleichung verlangt, erscheinen zwei Faktoren, und die Potenz ist um Zwei gesunken.
Jetzt wirds spannend, denn für jede Potenz der Reihe von Teilfunktionen soll das gelten, dass genau wieder ein Glied dieser Reihe entsteht, das vorher schon da war, aber jetzt mit negativem Vorzeichen. Das Quadrat welcher Zahl ist -1? Wir brauchen also die imaginäre Einheit i. Für den physikalischen Prozess lassen wir den Imaginäranteil weg, da haben wir nur noch jede zweite Potenz übrig. Nun haben wir die Wahl: Nehmen wir alle geraden oder alle ungeraden Funktionen? Auch diese Frage lässt sich physikalisch beantworten: Starten wir im Gleichgewichtspunkt (also bei Null), nehmen wir die ungeraden, starten wir im Umkehrpunkt (also bei unserer Normierung der dimensionslosen Physik bei Eins), nehmen wir die geraden. Die Faktoren wählen wir so, dass sich die doppelte Multiplikation mit den Potenzen aufhebt. Und fertig ist die Summation der Funktionen, die die Bedingung der rücktreibenden Kraft erfüllt:
x(t) = t – 1/6*t^3 + 1/120*t^5 – 1/5040*t^7 + … + i^2n*1/((2n+1)!)*t^(2n+1) + …
Jetzt ist tatsächlich erfüllt, dass gilt:
x“(t) = -t + 1/6*t^3 – 1/120*t^5 + … = -x(t)
Nimmt man EXCEL zu Hilfe und zeichnet sukzessive die Entwicklung dieser Summe in ein Diagramm, erlebt man etwas zum Staunen: Die Überlagerung der in den rechten Quadranten wechselweise ansteigenden und abfallenden Funktionen ergibt eine Schwingung!

Entwicklung der Sinusfunktion aus der Potenzreihe bis zur 21. Potenz (blau: 1. Potenz, magenta: 1. und 3. Potenz, gelb: 1. und 3. und 5. Potenz usw. usf.) und Vergleich mit der „echten“ Sinusfunktion (rot) – der erste Nulldurchgang nach dem Ursprung liegt ab der Einbeziehung der 7. Potenz in der Nähe von 3,14… (!!) und wird dann immer genauer, ohne dass wir irgendwo Pi benutzt hätten!
Nun haben wir ganz nebenbei – bei der Behandlung einer physikalischen Frage! – die „Kreiszahl“ Pi entdeckt. Und: Was hat unser Ansatz mit der geometrischen Definition von Pi als Seitenverhältnis im rechtwinkligen Dreieck oder im Einheitskreis zu tun?
Der Kreis ist das Verbindende! Er ist die Überlagerung zweier Schwingungen, die senkrecht aufeinander stehen und gleiche Frequenz und gleiche Amplitude haben (sonst wird es eine Ellipse oder gar eine Rosette – Lissajous-Figur). Beschreibt man den Kreis über den Parameter t, der gern die Zeit darstellen darf, so kommt man über das Pi der Sinusfunktion wieder auf Pi, jetzt als Verhältnis von Halbkreisumfang und Radius. (Warum hat mir das keiner in der Schule erklärt??)
Um Pi möglichst genau zu bestimmen, können wir mit obigem physikalischen Ansatz nun so vorgehen, dass wir die erste Nullstelle der Reihenentwicklung der Lösungsfunktion der Schwingungsgleichung suchen, wobei wir die Anzahl der Glieder dieser Reihe so hoch wie möglich wählen. Wieso so hoch wie möglich?
Nun, weil es entweder eine Frage des Fleißes ist, wieviel Glieder (also bis zu welchem k mit k = 0, 1, 2, 3, …)
t^(2k+1)/(2k+1)! (Sinus) oder
t^(2k)/(2k)! (Cosinus)
wir „schriftlich“ mit einem Start-t von 3,0 berechnen wollen, um sie mit wechselndem Vorzeichen versehen zu addieren und mit Null zu vergleichen, um anschließend mit iterativ geändertem t fortzufahren, bis uns die Abweichung von der Nullstelle klein genug erscheint.
Für „faule“ ist es eine Frage des Geistes und der Programmier-Erfahrung, wie sie einem Rechner beibringen, mit mehr als den üblichen Stellenzahlen umzugehen. Ohne Extras kommt man in EXCEL auf 15 Stellen (10 werden aber normalerweise nur angezeigt!), wenn man die ersten 15 Glieder Sinus oder 12 Cosinus benutzt und tatsächlich bei einem Nullstellenfehler von etwa 3*10^-15 landet und den tatsächlich richtigen Wert
Pi = 3,141 592 653 589 79
erhält:
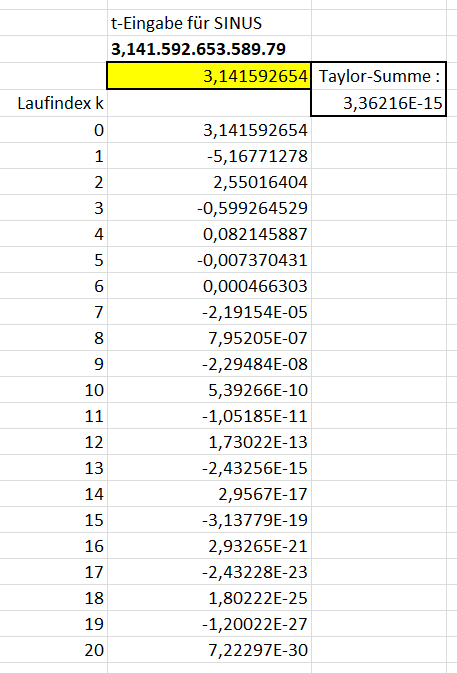
In die gelb unterlegte Zelle, mit der EXCEL rechnet, ist die darüberstehende, iterativ angepasste Zahl eingetragen worden. Die Taylor-Summe zeigt die Abweichung von Null an, mit deren Minimierung die Eingabe per Hand iteriert worden ist.
Das Spannende an dieser Herleitung von Pi ist, das dieses völlig unabhängig von der Größe der „Auslenkung“ aus dem Gleichgewicht und von der Größe der „rücktreibenden“ Kraft oder der Masse ist. Variiert man nur die Auslenkung, bleibt sogar auch die Dauer der Schwingung konstant, welche sich aus der Wurzel des Quotienten von Masse und Federkonstante ergibt (zweifache Integration, deshalb Quadrat-Wurzel).
Addiert man vektoriell zwei senkrecht zueinander stehende Schwingungen gleicher Amplitude und gleicher Schwingzeit bei einer Phasenverschiebung von einem Viertel der Schwingzeit, so erhält man einen Kreis. Dessen Umfang ergibt sich aus der Geschwindigkeit der Bewegung und der Zeit. Sind alle physikalischen Größen auf „1“ gesetzt, bleibt der mathematische Kreis mit einem Umfang von „2*Pi“, nämlich der zweiten Nullstelle der oben angeführten Potenzreihe, die zur Sinusfunktion führt.
Wenn man nun den „Winkel“ als Verhältnis eines Bogens zum Radius einführt, ist der Winkel des Vollkreises ebenfalls „2*Pi“.
Dass nun Pi auch bei der Kugel im Dreidimensionalen und weiteren Körpern im n-Dimensionalen auftreten muss, ist logisch.
Mich als Physiker beruhigt die Tatsache, dass Pi KEIN Hirngespinst der Mathematiker ist, sondern eine „natürliche“ irrationale Zahl.
(Übrigens: Die diversen Reihenentwicklungen oder unendliche Kettenbrüche oder unendliche Produkte für die Berechnung von Pi, die man in diversen Nachschlagewerken findet, entbehren dieses hier angeführten einfachsten physikalisch-philosophischen Ansatzes; erst recht die für die Computer-Berechnung von möglichst vielen Stellen von Pi entwickelten langzahlfähigen Algorithmen.)
Zusammen mit der Dämpfung (siehe „e: Universelle Naturkonstante aus der Dämpfungsgleichung für Anfänger„) hat man nun die zwei wichtigsten natürlichen und technischen zeitabhängig rückwirkenden Prozesse „im Griff“ und nebenbei die universellen Konstanten Pi und e endlich verstanden und nicht nur zur Kenntnis genommen.
Übrigens: Man kann alle drei Gleichungen (Dämpfung, Wachstum und Schwingung) mit der richtigen Verwendung der imaginären Einheit „i“ bzw. „j“ zusammenfassen, was besonders in der Elektrotechnik viele Vorteile bei der kompakten Beschreibung analoger Schaltkreise bringt. Interessenten informieren sich bitte dort – das führte hier zu weit von den Strukturen weg, pardon.
Kommentar abgeben