AAA 2: Statistik in Galaxien
Adolphis Astronomie-Abend 2
Bisher haben wir die radiale Geschwindigkeits-Verteilung von Sternen in Galaxien untersucht, wenn man vereinfachend von Kreisbahnen ausgeht, die untereinander wirken, als ob ihre Umgebung homogen wäre.
In Wirklichkeit aber wirken konkrete nahe Nachbarn stärker als viele ferne. Sofern sie nicht zusammenstoßen, ist ihre Wechselwirkung paarweise ohne Energie-Austausch, also so etwas wie „elastisch“. Aufs Gesamtsystem bezogen (also in einem anderen Koordinatensystem als dem des Paar-Schwerpunktes) gibt es allerdings einen Energie-Austausch, den man in erster Näherung mit dem von Gasteilchen eines „idealen“ Gases vergleichen kann.
Zur Veranschaulichung noch einmal ein Doppelstern aus einem vorbeifliegenden Raumschiff betrachtet:
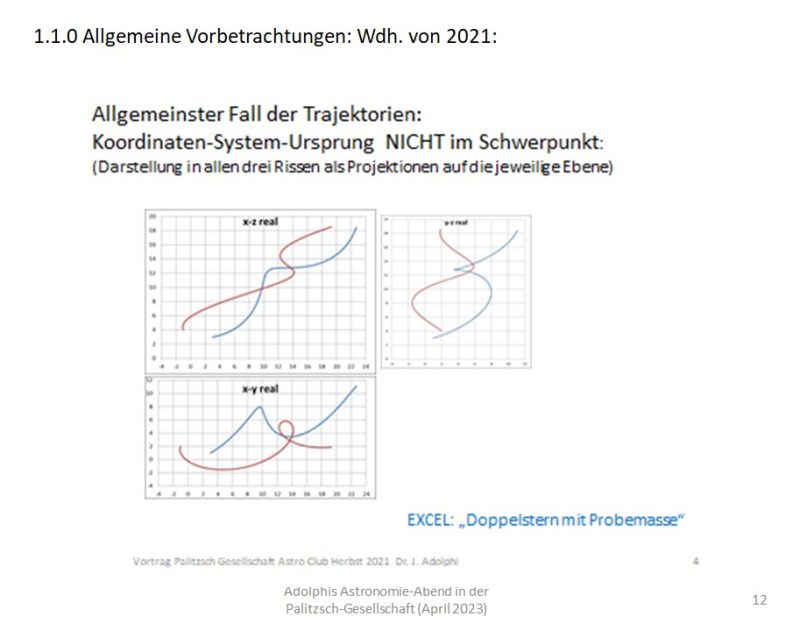
Man „sieht“, dass nicht ohne weiteres Ellipsen zu erkennen sind, wie es im Schwerpunktsystem ganz leicht wäre.
Will man nun einmal von Kepler absehen und eine Begegnung zweier Massen als „elstischen Stoß“ sehen, weil in ihrem Teilsystem ja keine Energie untereinander ausgetauscht wird (das passiert allerdings in einem relativ zum Schwerpunkt der beiden bewegten System, obwohl ihre Energiesumme auch dort konstant bleibt!!), so bietet sich an, beide elastischen Vorgänge einmal genauer unter die Lupe zu nehmen.
Im gebundenen Zustand erhalten wie eine Schwingung, die sich von der rein elastischen unterscheidet, wenn wir einmal eine gravitative Ellipse als radiale Schwingung verstehen und andererseits einen springenden Ball als zusammengesetzten Vorgang, nämlich elastische Beschleunigung n der Berührungsphase mit dem Boden nach oben und gravitative Beschleunigung ständig nach unten:
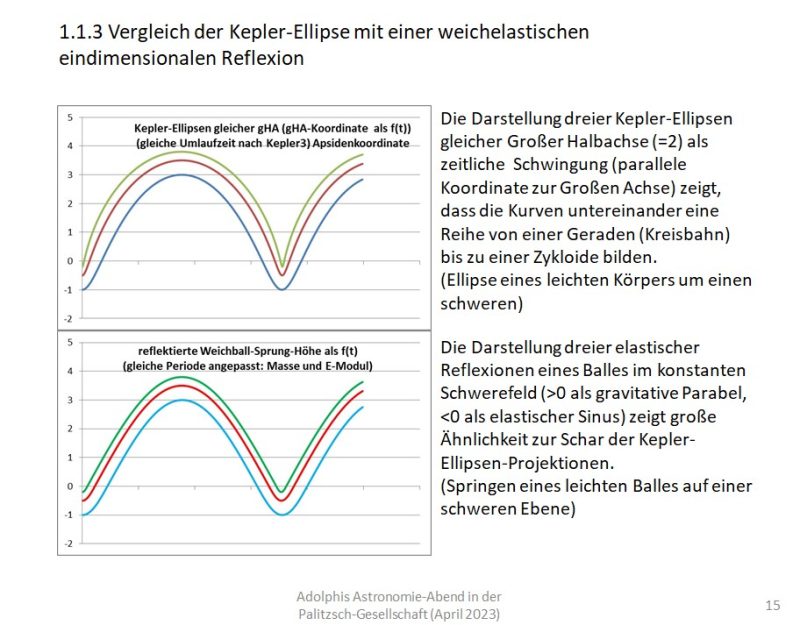
Im einzelnen sieht der Vergleich eines elastischen Stoßes zweier Kugeln mit dem hyperbolischen „Vorbeifliegen“ zweier schwerer Punktmassen so aus:
Zuerst der elastische Stoß zweier Kugeln auf einer Platte oder auch im Raum:

Hier stoßen zwei unterschiedlich schwere und unterschiedlich schnelle Kugeln elastisch zusammen (blaue ist leichter). Man sieht, wie die Winkel vom Koordinatensystem abhängig sind, von dem aus man den Stoß beobachtet!
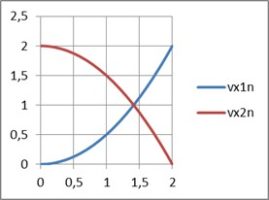
Zeichnet man eine Funktion der Abhängigkeiten der Geschwindigkeit und des Winkels vom „Stoßparameter“, so erhält man folgendes Bild für die stoßende der zwei gleich schweren Kugeln, von denen die andere vor dem Stoß ruht:
w = π – 2*arcsin(b/2r) = π – 2*arcsin(p)

Splittet man den Vorgang weiter auf und betrachtet beide Kugeln, ergeben sich folgende Bilder (wieder zwei gleich schwere, eine davor ruhend, also nur die x-Komponente der stoßenden ist vor dem Stoß ungleich Null):
Verändert man das Masseverhältnis, ergibt sich folgende Kurvenschar für die stoßende Kugel (Stoßparameter auf d bezogen, nicht auf r, Massenanteil an Gesamtmasse [0,5 ist also gleich schwer, so wie oben]):
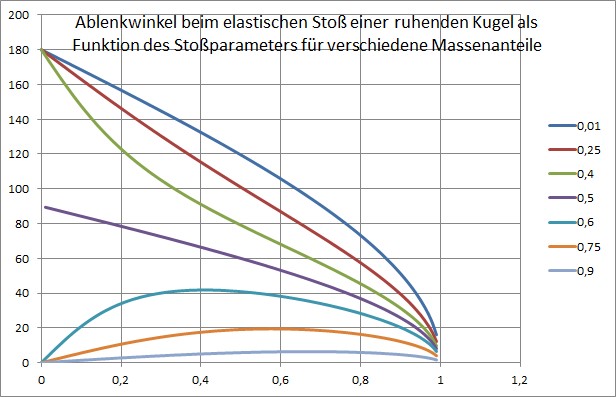
Zusammengefasst heißt das:
Da selbst im symmetrischen Fall eines elastischen Stoßes je nach Bezugssystem alle möglichen Geschwindigkeiten und Winkel vorkommen können, kann man eine Ansammlung elastisch stoßender Körper mit statistischen Methoden beschreiben, wie es beim idealen Gas üblich ist. (Körper mit inneren Freiheitsgraden nehmen eine zusätzliche Energieart auf, deren Wirkung in der Theorie der spezifischen Wärme gut beschrieben ist. Hier beträfe das Doppelsterne und ähnliche Gebilde…)
Jetzt der gravitative Fall:
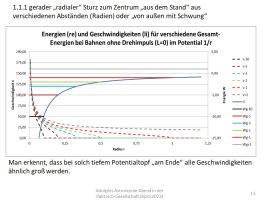
Im Falle eines schweren Zentrums mit dem kugelsymmetrischen Potential 1/r kann man das grafisch so darstellen:
Die Energie-Erhaltung wird durch die waagerechten Balken dargestellt. Deren Abstand zur Potentialkurve symbolisiert die kinetische Energie. Die dazugehörigen Geschwindigkeiten sind aus den Kurven abzulesen. Für L>0 und Wges>0 ergeben sich radiale (elliptische) Schwingungen, für Wges>0 ein (hyperbolischer) Vorbeiflug. In einem animierten Modell-Programm sieht das so aus (jeweils Periapsis oder Geschwindigkeit variiert):

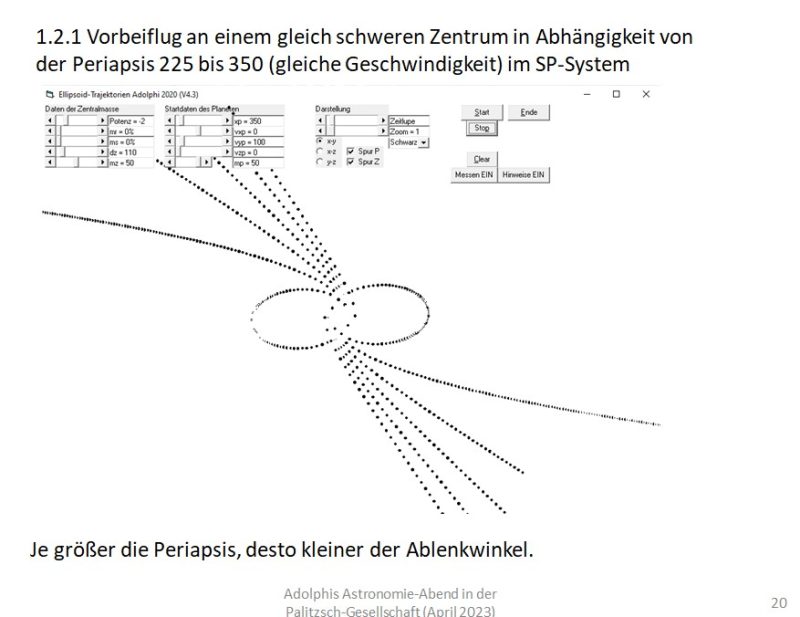
Man erkennt, dass sowohl der Zantralabstand („Stoßparameter“ oder Persiapsis) als auch die Geschwindigkeit (Gesamt-Energie) eine große (und ähnliche!!) Rolle spielen. Fasst man das in einem Diagramm zusammen, ergibt sich folgendes Bild:
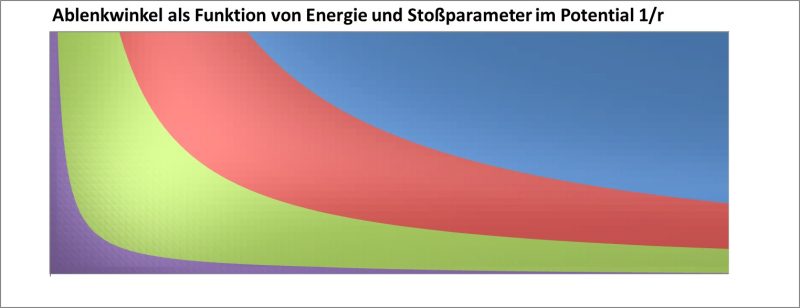
Zusammengefasst heißt das:
Wie beim mechanischen elastischen Stoß ergeben sich weite Spielräume für Winkel- und Geschwindigkeitswerte. Nimmt man eine genügend große Zahl von Massen in einem Sternhaufen an, kann man mit statistischen Methoden arbeiten. Zusätzlich zu den rein elastischen Stößen mit den nächsten Nachbarn bestimmen auch Fernwirkungen (Gravitation!) und Scheinkräfte (Corioliskraft) die „absoluten“ und „relativen“ Bewegungen, so dass eine gewisse „Stapelung“ entsteht, die entfernt an die Erdatmosphäre erinnert, die hier von unten geheizt wird:
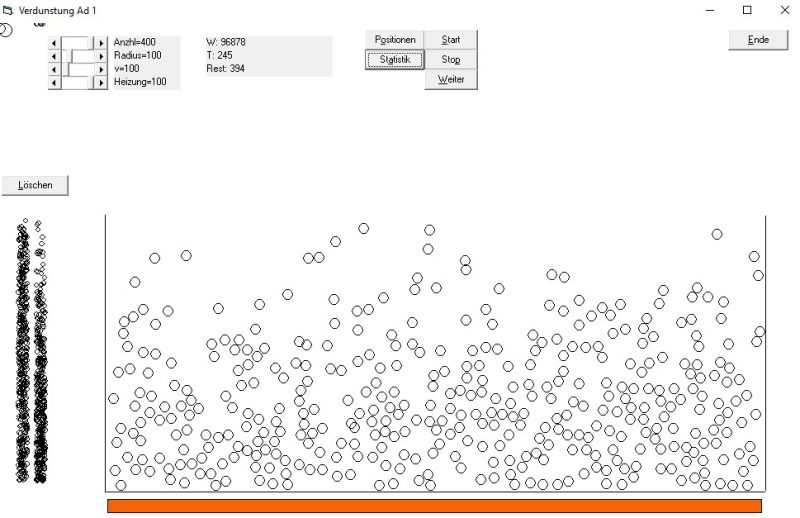
Ideales Gas unter Schwerkraft und Bodenheizung
Links ist die Gleich-Verteilung vor dem Programm-Start mit der aktuellen Höhen-Verteilung verglichen. (Man ahnt, dass es ähnlich der „barometrischen Höhenformel“ beschreibbar wäre.) Durch Stöße ist auch zufällig ein Entweichen nach oben möglich. Im Weltall würde sich dort ein Gleichgewicht zwischen Verlassen und Einfangen einstellen können…
Die Idee, Sternhaufen mit statistischen Methoden beschreiben zu wollen, ist also nicht vorn vornherein abwegig!




Kommentar abgeben