2.10.1 Flusspegel
Kann man den Pegel eines Flusses längs seines Verlaufes vorausberechnen, wenn man einen bestimmten Durchfluss annimmt?
Diese Frage klingt sehr einfach. Wenn man „es sich einfach macht“, ist es das auch, aber dann stimmt es eventuell mit der Realität nicht überein.
Wo aber fängt man am besten mit dem Vereinfachen an, um sich schrittweise an die Lösung heranzupirschen?
Oder andersherum, wie stets auf dieser Seite: Wie baut man schrittweise ein Modell auf? Was sind die einfachsten und sichersten Zusammenhänge, die man erkennen kann? Kommt man ohne Literatur- oder Internet-Recherche ganz allein auf wenigstens näherungsweise vernünftige Ergebnisse?? (first principles)
(Es wäre auch nicht schlecht, den „stationären Zustand“ als eine andere Art „stehender Welle“ zu begreifen, nämlich eine Welle, die flussauf mit der Fließgeschwindigkeit wandert, also relativ zum Ufer „steht“, wie das jede Boje im Fluss deutlich zeigt. Sollte man sich da vorher noch einmal mit Wellen überhaupt beschäftigen? Siehe also eventuell Unterpunkt 2.10.1.1!)
a) Die Hangabtriebskraft
Man weiß aus Erfahrung, dass Wasser nicht bergauf fließt, sondern bergab. Per Schlitten oder Ski oder per Fahrrad oder Skateboard kommt man umso schneller bergab in Fahrt, je steiler der Berg ist. Man könnte also eine beschleunigende Kraft aus der Masse des Wassers und der Hangneigung formulieren.
ABER: Man weiß durch Spielen am Bach (Staudamm-Bauen), dass die Fließgeschwindigkeit auch vom Wasserstand abhängt.
b) Die Reibung
Das Wasser reibt sich am Grund und an sich selbst. Es entsteht also ein Geschwindigkeits-Profil im Wasser selbst. Idealerweise nimmt man an, dass am Grund die Geschwindigkeit Null ist und an der Oberfläche am größten. Der Unterschied von Schicht zu Schicht teilt sich dann auf die gesamte Wasserhöhe gleichmäßig auf. Der Differentialquotient dv/dh ist dann nur von der Neigung des Grundes und der Zähigkeit des Wassers abhängig. Dann ist die Fließgeschwindigkeit an der Oberfläche vom Wasserstand, der Neigung und der Zähigkeit abhängig.
c) Die Mengen-Bilanz
Wollen wir einen „stationären“ Zustand beschreiben, also einen Zustand, der sich zeitlich nicht ändert, so muss in jedem Querprofil des Flusses die gleiche Menge Wasser pro Zeit vorbeikommen.
Da wäre also zum Beispiel mit dem so genannte Kontinuitäts-Gesetz, repräsentiert durch die Kontinuitäts-Gleichung, zu beschreiben. Es besagt, dass die zeitliche Änderung einer Erhaltungsgröße mit der Differenz zweier Ströme (Zu-Strom und Ab-Strom) proprotional verknüpft ist. Im Proportionalitätsfaktor steckt die Geometrie der Anordnung. Daraus folgt im stationären Zustand einer inkompressiblen Flüssigkeit, dass das Produkt von durchströmtem Querschnitt und über den Querschnitt gemittelter Strömungsgeschwindigkeit an allen Orten gleich sein muss.
Beispiel: Stehender zylindrischer Wasserbehälter mit Zustrom oben und Abstrom unten. Je nach Querschnitt des Behälters ändert sich der Wasserstand bei gegebenem Strom-Unterschied schneller oder langsamer. Schon dieses Beispiel ermöglicht bei gegebenem Zustrom und Wasserstands-abhängigem Abstrom (Druckabhängigkeit) einen Ausgleichsprozess mit dem Ergebnis eines stationären Zustands.
Die dazugehörige Gleichung wäre (h: Pegel, t: Zeit, Q Wasser-Volumen-Strom, A: Querschnitt)
dh/dt = (Qzu-Qab)/A
Für dh/dt = 0 ist dann Q überall gleich.
Für einen echten Fluss in der Landschaft ergeben sich nun mindestens zwei kleine Komplikationen selbst im stationären Zustand:
Erstens ist der „Querschnitt“ nach oben (räumlich gemeint!) und zu den Seiten offen, besser formuliert: Das Flussbett (samt Überflutungsgebiet) hat an jeder Stelle ein anderes Profil.
Zweitens ist die Strömungsgeschwindigkeit an jeder Stelle des jeweiligen Profils unterschiedlich, und das auch noch komplex pegelabhängig, also nicht mit einem Proportionalitäts-Faktor allein zu beschreiben.
Wollte man das Ganze durch eine elektrische Widerstand-Modellierung beschreiben, hätte man ein kompliziertes Netzwerk (Reihenschaltung von Parallelschaltungen) mit stromabhängigen Einzel-Widerständen, dem man einen Gesamt-Strom aufprägt und dann die Potentiale längs des Haupt-Pfades bestimmt.
In der Praxis wird deshalb versucht, eine Datenbank von Messwerten (Luftbilder der Überschwemmungsgebiete) aufzubauen, mit deren Hilfe man Voraussagen treffen kann.
Für einen einzigen Ort des Flusslaufes macht man im einfachsten geometrischen Fall (flaches Kastenprofil, also Vernachlässigung des Randes) folgende Annahme: Die innere Reibung des Wassers führe zu einer linearen Verteilung der Fließgeschwindigkeit von Null (Grund) bis zum Maximum (Oberfläche). Dann ergibt sich eine quadratische Abhängigkeit von Pegel h und Durchfluss Q (k: Konstante, die die innere Reibung und das Gefälle enthält, y:Breite):
Q = k*y*h²
Könnte man nun (stark vereinfacht!!) diesen Ansatz über den gesamten Querschnitt s(y) des Flusses additiv überlagern, ergäbe sich
Q = k* ʃ (h-s(y))² dy
(Hier wäre also die innere Reibung quer zur Hauptströmungsrichtung in waagerechter Richtung vernachlässigt und nur senkrecht berücksichtigt!! Makroskopische Wirbel gäbe es also überhaupt nicht.)
Aber selbst mit diesem sehr-sehr stark vereinfachten Ansatz müssten wir jetzt noch sehr-sehr viel rechnen, denn unser Anliegen ist ja, den stationären Zustand in Längs-Richtung des Flusses zu bestimmen. Neben dem ortsabhängigen Querprofil für jeden Fluss-Meter brauchen wir nun auch noch die Längsverknüpfung der Profile. Dann können wir mit der zeitabhängigen Kontinuitätsgleichung (s.o.!) numerisch rechnen und die Rückkopplung zwischen Q(x) und h(x) für alle x so lange betreiben, bis Q(x) = const („x-unabhängig aufgeprägter konstanter Gesamt-Strom“) herauskommt.
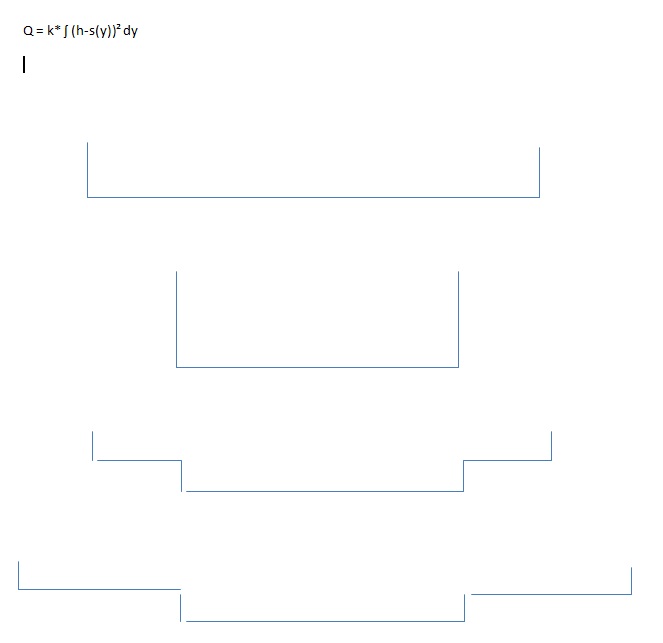
Ob wir das hinkriegen, ganz einfach einmal für konstantes Längsgefälle und in Längsrichtung 4 verschiedene Querschnitte (unter Vernachlässigung der Querschnitts-Übergänge und der dort zu erwartenden Wirbel!)?
Die Gleichung für den Zusammenhang zwischen Pegel (in der Mitte gemessen) und Durchfluss verändert sich von oben nach unten angepasst zu (y: Breite Hauptkasten, ys: einfache Breite Nebenkasten, x: Stufenhöhe über Hauptkasten):
Q1 = k1 * y1 * h1²
Q2 = k2 * y2 * h2²
Q3 = k3 * (y2 * h3² + 2*ys3*(h3-x3)²)
Q4 = k4 * (y2 * h4² + 4*ys3*(h4-x3)²)
Was steckt eigentlich in den k? Da muss die Viskosität des Wassers enthalten sein und aber auch das Gefälle des Flussbetts! Lassen wir beides konstant, könnten wir das Gleichungssystem analytisch lösen, wenn alle Q ebenfalls gleich sind. Dann hätten wir 4 Gleichungen für 4 h.
h1 = √(Q/(k*y1))
h2 = √(Q/(k*y2))
h3 = 2*ys3*x3/(y3+2ys3) + √[(2*ys3*x3/(y3+2ys3))² + (Q/k – 2ys3*x3²)/(y3+2ys3)]
h4 = 4*ys3*x3/(y3+4ys3) + √[(4*ys3*x3/(y3+4ys3))² + (Q/k – 4ys3*x3²)/(y3+4ys3)]
Denkste!
Wie man ohne zu rechnen erkennt, wäre der Pegel im zweiten Abschnitt höher als im ersten, was zwar mathematisch richtig, physikalisch aber unsinnig wäre.
Das bedeutet, dass unser Modell von dem hier verwendeten mathematischen Ansatz unvollständig beschrieben ist. Wir müssen zusätzlich noch eine Wechselwirkung zwischen den einzelnen Flussabschnitten einbauen, Ausgleichs-Ströme nämlich. Und diese sind nicht von der Höhe über dem Untergrund (h) abhängig, sondern von der Differenz der absoluten Höhen über NN.
Dann können wir die Iteration ruhig mit dem falschen Start-Set beginnen und ans darauf verlassen, dass sich alles „einpegeln“ wird, nämlich auf gleiche innere wie äußere Ströme. (Man kennt das von der Wärmeleitung: Wärmedurchgang und Wärmeübergang immer abwechselnd als Reihenschaltung bei der Dämmungsberechnung!)
Welchen Ansatz wählen wir für die Ausgleichsströme?
Auch hier wäre ein qaudratischer Ansatz sicher denkbar, aber da sich der hydrostatische Druck proportional zur Schichtdicke erhöht, ist wohl ein Produkt von Pegel-Differenz und Pegel selbst das Bessere (ist in der Dimension auch wieder quadratisch!), denn der Druckunterschied wirkt über den gesamten Pegel. (Die Stufenform unsereres numerisch getakteten Ansatzes lassen wir wieder näherungsweise außer Acht.) Der Proportionalitätsfaktor des Ansatzes kann dann beim „Spielen“ angepasst werden, denn in ihm steckt auch das Volumen des jeweiligen Profil-Abschnitts, also dessen Länge.
Ein einfaches Zahlenbeispiel für die oben skizzierten Profile soll das veranschaulichen (das erste Profil wird als fünftes wiederholt):
Bei einem Strom von 1000 m³/s und einer Basis-Breite von 100 m sowie einer Basis-Stufen-Breite von je 10 m seitlich ergeben sich bei einem linearen Profil der Strömungsgeschwindigkeit folgende ortsbezogenen Pegelhöhen hi:
| h1 | h2 | h3 | h4 | h5 |
| 2,89 | 3,16 | 3,03 | 2,92 | 2,89 |
Da das Wasser aber nicht „bergauf“ fließen wird (z.B. von Abschnitt 1 mit 2,89 m nach Abschnitt 2 mit 3,16 m), muss es vor Abschnitt 2 einen „Stau“ geben, wie man das als stromauf zeigende „Bugwellen“ an Brückenpfeilern kennt. Dadurch wird das Gefälle unter der Brücke größer, sodass die gleiche Wassermenge pro Zeit durch die Brücke (also durch eine verringerten Breite) fließen kann wie vor ihr und nach ihr.
Wenn wir also idealerweise einen Fluss-Grund mit konstanter Neigung in Fließrichtung annehemen, wird die Fluss-Oberfläche NICHT PARALLEL zum Flussgrund verlaufen, der lokale Pegel als schwanken, und damit die „Uferlinie“ bei Überschwemmungen die Isohypsen der Uferzone anders schneiden als bei Parallelität zum Fluss-Grund.
Das ist übrigens auch die Ursache dafür, dass das Ausbaggern an einzelnen Stellen nur sehr geringe Auswirkungen auf den Hochwasserverlauf hat, da es sich (einmal „elektrisch“ gesprochen) nur um das Parallelschalten von kleinen Speichern (Kondensatoren im Gleichstromkreis) handelt, die im Nu aufgefüllt sind und lediglich eine kleine lokale und geglättete „Delle“ im Pegelverlauf erzeugen können. (Offenbar bilden sich in solchen Löchern spannende Wirbel aus, wenn gleichzeitig eine Krümmung des Wasserlaufes vorliegt. Das kenne ich von der Müglitz, wo mancherorts der Flusskrümmungsradius vorm Prallhang in der Größenordnung der Flussbreite liegt und diese Löcher dann geröllfrei bleiben, was den Steinesucher natürlich erfreut: Die Achate liegen auch noch hinter den Löchern!…) Der „Wasserwall“ vor kleinbogigen Brücken mit dicken Pfeilern kann ziemlich groß werden und die anströmigen Uferpartien beeinträchtigen oder die Brücke durch den einseitigen Druck zerstören.
Zwischenfazit:
Die halbquantitative „nullte Näherung“ des Modell-Ansatzes zeigt, dass man selbst im stationären Fall (also mit der Kontinuitätsbedingung) mehrere Dinge im „richtigen“ Modell beachten muss:
– Längsprofil des Flussgrundes
– Querprofil des Flussgrundes in möglichst kurzen Abständen („finite Elemente“!)
d) Neuer Ansatz über das Oberflächen-Längs-Profil des Flusses
Bevor wir neue Modell-Ansätze prüfen. müssen wir aber noch eine andere Frage beantworten:
Wie verhält es sich eigentlich unter c) mit den Geschwindigkeiten v0 in den einzelnen Abschnitten? Sie hängen doch von den Querschnitten ab!
| v0 / m/s | 2,89 | 3,16 | 2,91 | 2,71 | 2,89 |
| A0 / m² | 346,4 | 316,2 | 343,5 | 368,8 | 346,4 |
| t | h1 | h2 | h3 | h4 | h5 |
| 0 | 2,89 | 3,16 | 3,03 | 2,92 | 2,89 |
Also: Neben den Pegeldifferenzen treten auch noch Geschwindigkeitsunterschiede auf, die nach dem Trägheitsgesetz nur durch entsprechende Kräfte realisiert werden können.
Die oben pauschal eingeführte Konstante k sollte sich also bis auf die innere Reibung analytisch so auflösen lassen, dass man nicht eine Art „Hangabtriebskraft“ über dem fallenden Flussgrund nutzt, sondern eine Kraftdifferenz aus dem hydrostatischen Druck aufbaut, die eine Wassermasse beschleunigt. Im stationären Fall wäre dann zwar die zeitliche Änderung der Geschwindigkeit in jedem Ort Null, wobei für jeden Ort aus dem Profil eine spezielle pegelabhängige Reibungskraft zu berechnen wäre, aber das „Längs-Profil“ der Geschwindigkeit wäre nun keine Konstante mehr!
Die wirkende Kraft aus dem hydrostatischen Druck wäre das „Tiefen“-gewichtete Profil-Flächen-Integral über jeden Flussquerschnitt, die beschleunigende Differenz würde „vor“ und „nach“ einer Elemente-Grenze bestimmt werden. Nach kurzer Überlegung erkennt man wegen der Linearität der Druckabhängigkeit von der Tiefe, dass lediglich der Pegel-Unterschied mit dem Pegel selbst multipliziert (besser mit der Wassertiefe, und dann über das Querprofil integriert) diese Kraft ergibt. (Ihre Gegenkraft wäre die Reibungskraft des Wasserstroms. Die Resultierende aus beiden ergibt dann die Ursache für Beschleunigungen.)
(Es wird nun auf einmal richtig kompliziert, ohne dass wir schon Querbewegungen des Wassers berücksichtigt hätten…)
Nun könnten endlich alle finiten Längs-Elemente in Wechselwirkung treten.
(Fortsetzung folgt)
e) Berücksichtigung des Oberflächen-Quer-Profiles
(kommt)
f) Berücksichtigung von Kurven des Fluss-Laufes
(kommt)
Kommentar abgeben