2.8.8 Sichtbare Trajektorien: Spuren
Kann man interessante Spuren finden, wenn man zum Beispiel mit einem Fahrzeug solche hinterlässt und dabei sowohl mit der Geschwindigkeit des Fahrzeugs als auch mit dem Lenkradeinschlag spielt?
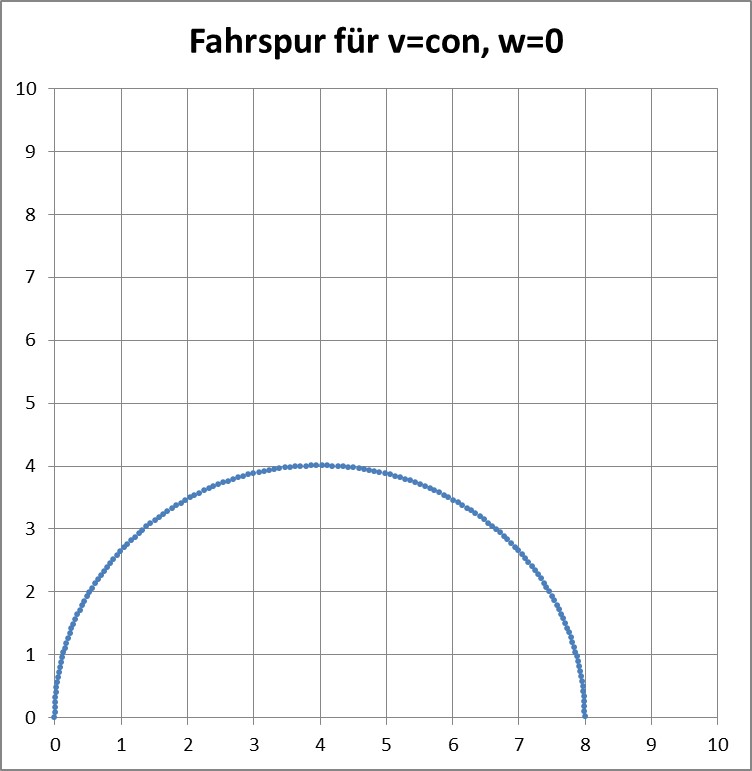
Der einfachste Fall wäre eine konstante Geschwindigkeit und ein konstanter Einschlag:
Es sollte sich ein Kreis ergeben. Warum?
Konstanter Einschlag des Lenkrads heißt konstante Krümmung. Das wäre sogar unabhängig von der Geschwindigkeit ein Kreis, solange das Fahrzeug nicht „aus seiner Spur ausbricht“.
Man sollte diese Parameter trotzdem durchspielen, um sicher zu sein, dass das kleine VBA-Programm für EXCEL im einfachsten Fall keine Fehler zeigt:
Kreisbogen bei konstanter Geschwindigkeit und konstanter Lenkradstellung
Wenn man bei konstanter Geschwindigkeit das Lenkrad gleichmäßig dreht, sollte man auf eine Kurve kommen, deren Krümmung sich kontinuierlich verstärkt, deren Radius sich also kontinuierlich verkleinert.
Gibt es für diese Kurve schon eine Bezeichnung?
Ja, das ist die klassich „Klothoide“ genannte Euler-Spirale. Ihre Krümmung wächst proportional mit der Bogenlänge (von einem geraden Start gerechnet).
Bei uns soll die Geschwindigkeit konstant sein, weshalb Zeit(t)- und Bogenlänge(s)-Abhängigkeiten bis auf einen festen Proportionalitätsfaktor (die Geschwindigkeit als ds/dt) zur gleichen Kurve führen müssen.
Das ist für unsere Spielerei sehr praktisch, denn am Lenkrad wollen wir in unserem Experiment zeitabhängig drehen. Hier wäre das also ein zeitlich konstante Winkelgeschwindigkeit am Lenkrad. (Die Lenkrad-Übersetzung spielt dabei als konstanter Faktor ebenfalls mit, verändert aber wiederum den Kurven-Typ nicht. In der echten Fahr-Praxis allerdings passt man die Lenkrad-Stellung der gewünschten lokalen Krümmung an, nicht der Zeit!! Auf diesem Wege wird jeder Abweichung von der gewünschten Spur regelnd entgegengewirkt – Aufgabe für das „autonome Fahren“.)
So sieht die Spur dann aus (Punkte in konstanten Zeitabständen gezeichnet):
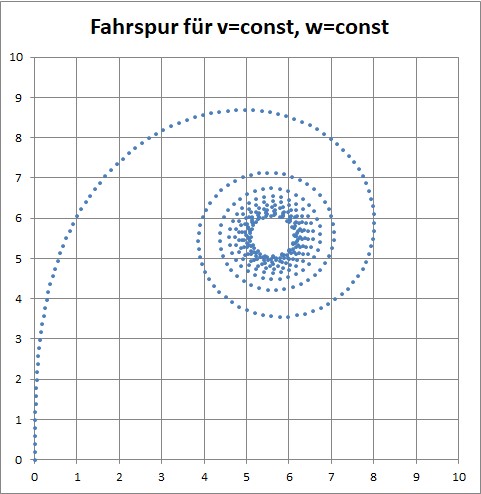
Fahrspur bei konstanter Fahrzeug-Geschwindigkeit v und konstanter Lenkrad-Winkelgeschwindigkeit w (Darstellung dort abgebrochen, wo sie zu verschmieren beginnt)
Nun kommen wir zur ersten Abweichung: Wir treten mit konstanter Kraft auf die Bremse (Luftwiderstand mal weggelassen), was die Geschwindigkeit zeit-proportional bis zum Stillstand verringert. Wie sieht die Spur jetzt aus?
Konstant abnehmende Fahrzeug-Geschwindigkeit bei konstanter Lenkrad-Winkelgeschwindigkeit
Auf den ersten Blick sieht die Punktfolge nicht so aus, als ob die Geschwindigkeit konstant abnähme, aber das liegt daran, dass man nicht-animierte Diagramme unbewusst örtlich liest. Trotzdem erkennt man sofort den Unterschied, denn die zweite Spur nähert sich ihrem Spiral-Mittelpunkt schneller, weil die Krümmung jetzt überproportional zur Weglänge wächst.
Was passiert, wenn wir das Fahrzeug beschleunigen?
Beschleunigtes Fahrzeug mit konstater Lenkrad-Winkelgeschwindigkeit
Es erhöht sich der Eindruck, man würde auf einen konstanten Kreis einschwenken, was aber ein Trugschluss ist, denn wir drehen ja weiter am Lenkrad. (Irgendwann wird aber die Führungskraft unserer Reifen überfodert werden…)
Man kann diesen Fall noch verstärken, indem man beschleunigt am Lenkrad dreht:
Sehr schnelles Eindrehen der Spur bei sowohl beschleunigtem Fahren als auch beschleunigtem Eindrehen des Lenkrads
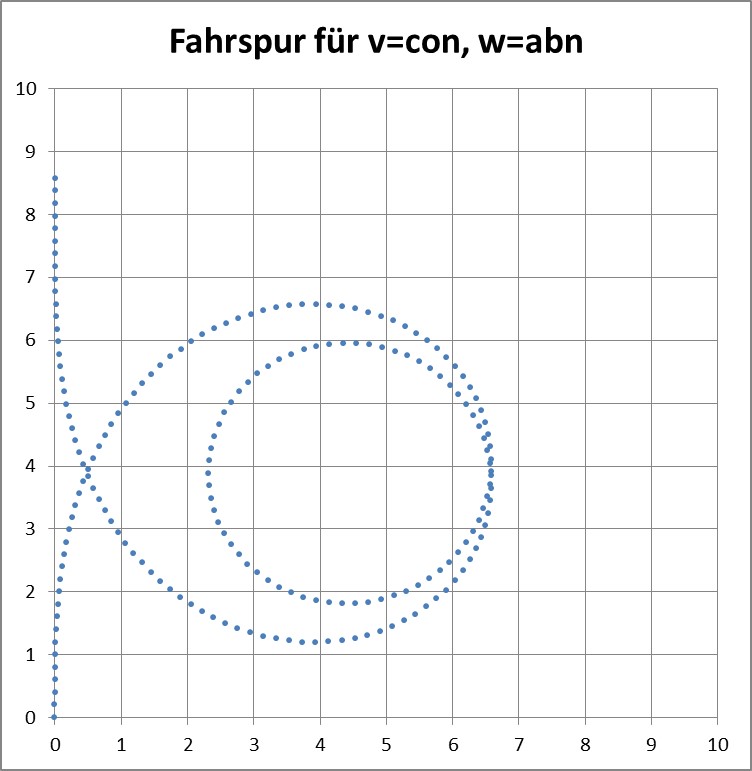
Nun wollen wir einmal die Winkel-Geschwindigkeit des Lenkrads ändern, und zwar gegen die anfängliche, und es ergibt sich eine Auflösung des ersten Eindrehens hin zu einem entegegengesetzten:
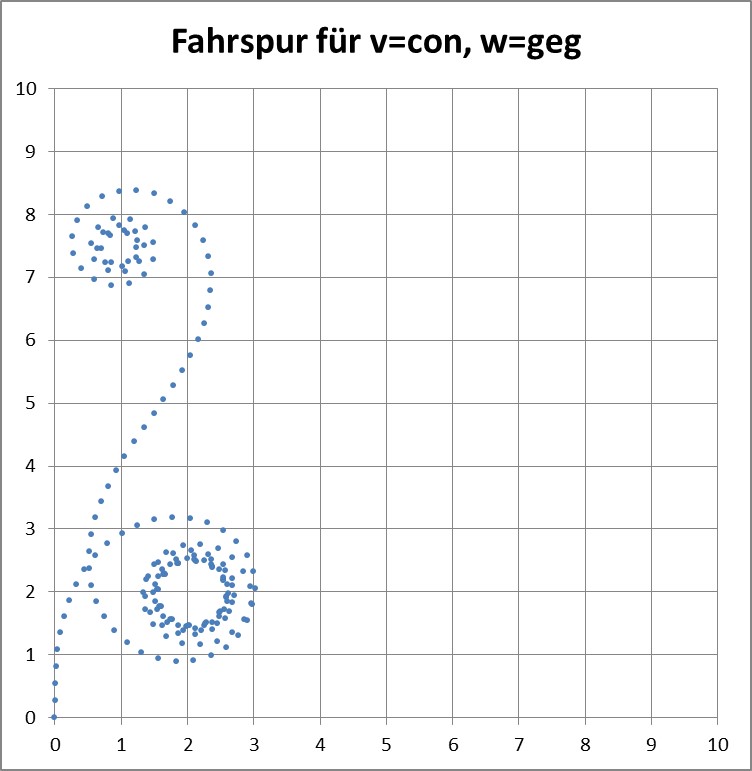
Allgemeine Kurve der Fahrzeugspur beim Verringern der Lenkrad-Winkelgeschwindigkeit bis in die entgegengesetzte Richtung
Durch Spielen kann man hier ein Werte-Tripel bei der konstanten Fahrzeug-Geschindigkeit finden (v, wo, dw/dt), bei dem ein parallel zur kartesischen Achse symmetrisches Bild entsteht:
Symmetrisches Sonderfall für konstantes Drehen am Lenkrad bei konstanter Fahrzeug-Geschwindigkeit
Wer das Ergebnis verwirrend findet, sollte daran erinnert werden, dass wir beim Drehen des Lenkrads bei Geradeaus-Stellung schnell beginnen und dann mit dem Drehen langsamer werden, bis wir schließlich wieder beschleunigt zurückdrehen (hier bei Geradeausfahrt „abgebrochen“, weil weitere Fahrt im anderen – nicht dargestellten – Quadranten stattfindet). Die Krümmung der Kurve (Stellung des Lenkrads) entspricht also dem Zeitintegral der Lenkradbewegung.
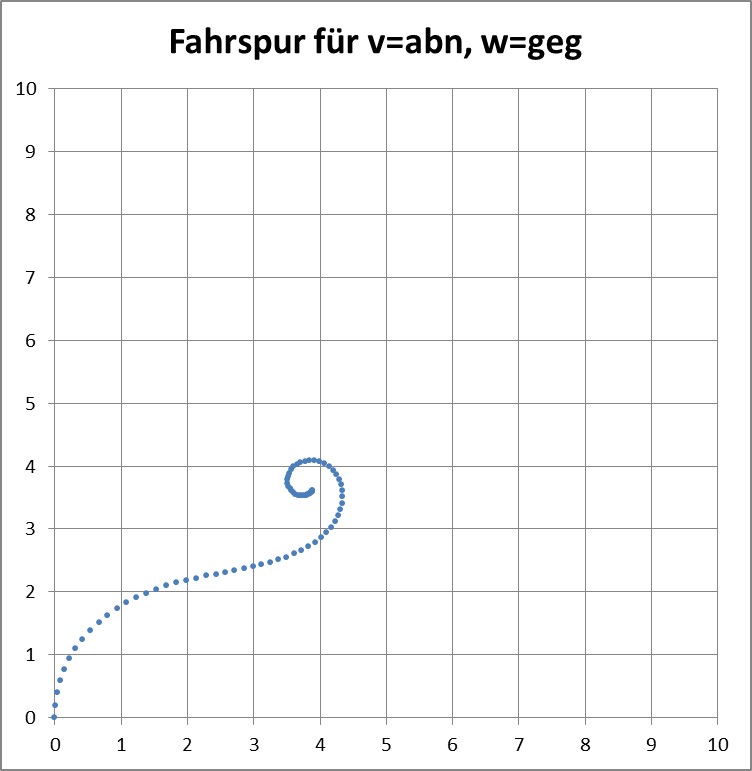
Würden wir in diesem Fall die Geschwindigkeit des Fahrzeugs kontinuierlich verringern, ergäbe sich folgende Kurve bis zum Stillstand:
Bremsen und am Ende gegensteuern
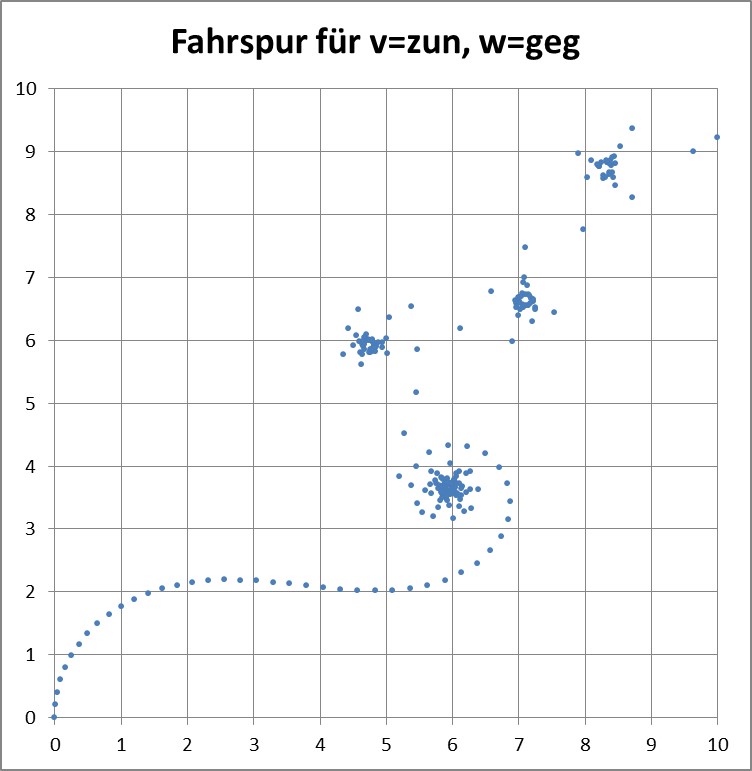
Würden wir aber beschleunigen, so kann folgende Grafik entstehen, die allerdings erläuterungswürdig ist:
„Schleudern“ als Artefakt des VBA-Programms
Das Schleudern und „Sichfangen“ das Fahrzeugs entsteht durch schlecht verarbeitete Winkelfunktionen, wodurch eine „Übersteuerung“ in einem einzigen Zeittakt entsteht, wobei die Takt-Winkel-Änderung jedesmal um 2*pi verringert wird.
Es gibt noch einen anderen symmetrischen Fall, der in der Praxis eine große Bedeutung hat: Zwei Klothoiden, die zu einem Kurvenzug zusammengesetzt sind, der beim Schienen- und Straßenbau verwendet wird, um möglichst geringe seitliche Kraftänderungen (Zwangskräfte auf Fahrzeuge und Passagiere) zu erzeugen (wird u.U., z.T. aus anderen Gründen, auch im Rennsport angestrebt):
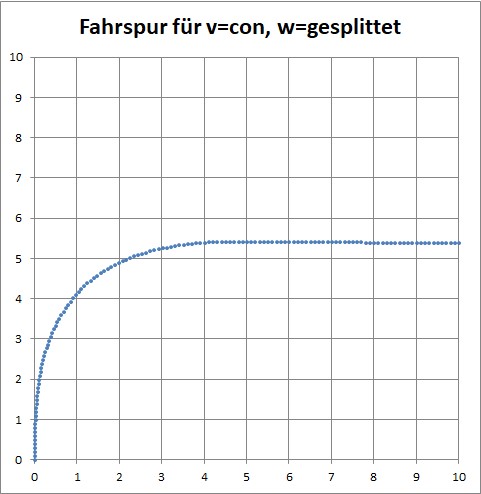
Zusammengesetzte Klothoide (hier zu 90-°-Kurve), um seitenkraftsprungfrei (also mit stetiger Seiten-Kraft-Änderung!) durchfahren werden zu können: Die konstante Lenkrad-Winkelgeschwindigkeit wird im Scheitelpunkt umgekehrt.
Hier zum Vergleich die gleichen Parameter, aber ohne Umkehr der Lenkrad-Winkelgeschwindigkeit (im so entstehenden Scheitelpunkt):
Klothoide, aus der das vorige Bild zusammengesetzt worden ist
Man kann sich vorstellen, dass man dieses Spiel noch weit ausbauen kann. Will man „Ernst“ machen, kann man ja das autonome Fahren simulieren, indem man vorgegebene Strecken möglichst genau nachfährt und dabei maximale Zwangskräfte (Reifenreibung in Fahrtrichtung und senkrecht dazu) und Drehmomente oder Leistungen drehzahlabhängig berücksichtigt. Der nächste Schritt wären dann unvorhergesehene bewegliche Hindernisse…
Der bisherige VBA-Code war sehr einfach aufgebaut (mehrfache numerische Integration):
Nicht wundern, aber r ist bei negativem beta (Lenkrad-Winkel) ebenfalls negativ, weil dann eine Gegenkurve gefahren wird. Auch alpha (Fahrtrichtung) kann dann natürlich negativ werden. Negatives v und damit auch ds ist hier bedingt ausgeschlossen worden, um mit den Umkehrpunkten keine Verwirrung zu erzeugen. Beispiel mit Umkehrpunkt (also nach gebremstem Vorwärtsfahren beschleunigtes Rückwärtsfahren):
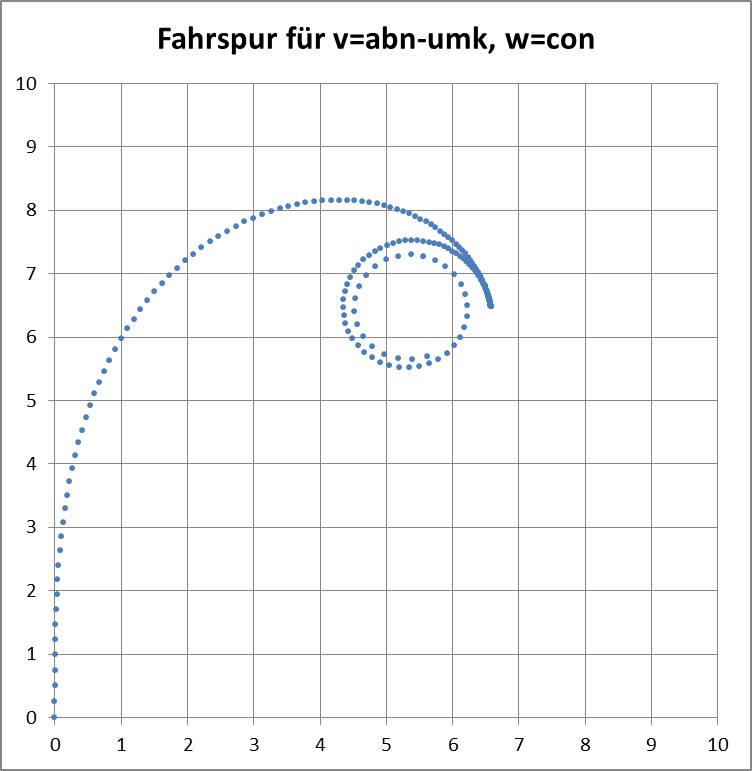
Beispiel mit negativer Beschleunigung samt Richtungsumkehr bei konstanter Lenkrad-Winkelgeschwindigkeit
Zusammenfassung:
Das Spiel mit zeit-, bogenlänge- oder ortsabhängig gekrümmten Fahrspuren ist interessant und durchaus ästhetisch. Für den Spezialfall der konstanten Geschwindigkeit ergibt sich die erfreuliche Situation, dass man bei einer entsprechend gebauten Klothoiden-Straße das Lenkrad gleichmäßig bewegen kann, was sowohl für den Fahrer als auch für die Fahrgäste (sie erleben keinen mechanischen „Stoß“ – eigentlich einen Kraft-Sprung, nämlich einen Übergang von seitlicher Kraft Null in einen endlichen Wert, wie das zum Beispiel bei einem selbst tangentialen Übergang in einen Kreisbogen der Fall wäre) sehr angenehm ist. Solche Kurven sind im modernen Schienen- und Autobahnbau seit über 80 Jahren zunehmend realisiert worden. (Ganz nebenbei schont es auch mechanische Teile der Fahrzeuge!)
Kommentar abgeben