Systematischer Symmetrie-Bruch: Praxis-Beispiele
Gibt es Praxis-Beispiele, wo ein Bruch einer Symmetrie systematisch erfolgt, also mathematisch beschreibbar ist?
Am leichtesten ist das wohl in der Kinematik zu studieren, in der (kräftefreien) Bewegungslehre (im Unterschied zur Dynamik, die die Kräfte als Ursache und Wirkung setzt), die eine Grundlage der Technischen Mechanik darstellt und deshalb überaus anschaulich ist.
Beispiel 1: Schubkurbel
Das klassische Beispiel ist die Schubkurbel, die einen Zusammenhang zwischen Drehbewegung auf dem Kreis und linearer Bewegung im Zylinder auf mechanische Weise erzeugt.
Die Kreisbewegung ist als Überlagerung zweier harmonischer Schwingungen zu verstehen, weshalb man vermuten darf, dass auch der Kolben im Zylinder eine harmonische Schwingung vollführt, oder? In meinem Alter hat man noch viele Erinnerungen an solche riesigen Kurbeln, die auf jedem Bahnhof zu bestaunen waren, wenn man an der Hand der Eltern oder Großeltern neben einer Dampflok stand: Von einem Gelenk an den riesigen Treibrädern der Lok ging eine dicke (oft rot lackierte!) Stange (Pleuelstange genannt) zu dem Gelenk an der Kolbenstange der Zylinder. (Die Treibräder waren auch untereinander gekoppelt.)
Sichere Behauptung 1:
Die Räder vollführen eine exakte Kreisbewegung im Bezugssystem der Lok, mit welcher ihre Achslager fest verbunden sind.
Sichere Behauptung 2:
Die Kolben vollführen eine exakte Linearbewegung im Zylinder.
Frage:
Wie ist der exakte Zeitablauf der Linearbewegung, wenn die Kreisbewegung mit konstanter Winkelgeschwindigkeit erfolgt? Ist er „harmonisch“?
Lösung:
Wir stellen einen geometrischen Zusammenhang zwischen dem Winkel der Kreisbewegung des Pleuelgelenks am Rad und dem Ort des Pleuelgelenks an der Kolbenstange auf und können unter der Bedingung einer konstanten Winkelgeschwindigkeit des Rades die Winkelabhängigkeit des Ortes der Kolbenstange in eine Zeitabhängigkeit transformieren und die Ort-Zeit-Funktion mit einer harmonischen Schwingung vergleichen.
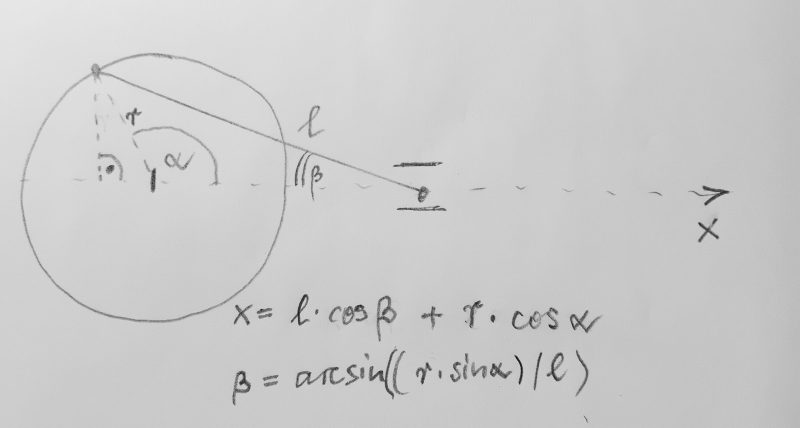
Handskizze zur Schubkurbel
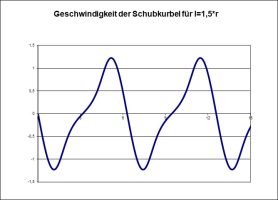
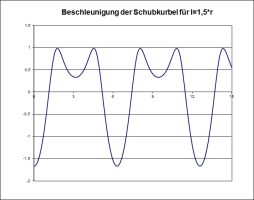
Rechnet man das durch, ergeben sich folgende Diagramme für den Ort des Kolbenstangen-Gelenks als Funktion des Winkels (im Bogenmaß), seine Geschwindigkeit und seine Beschleunigung:
Ort der Schubkurbel
Geschwindigkeit der Schubkurbel
Beschleunigung der Schubkurbel
Für ein sehr langes Pleuel wird beta Null, dann entshet eine harmonische Schwingung, wie im ersten Diagramm (Ort) zu erkennen ist, denn der Auslenkungswinkel aus der x-Achse, der die Unsymmetrie verursacht, verschwindet dann. Hier ist mit Absicht ein sehr kurzes Pleuel zur Verdeutlichung gewählt worden!
Die Unsymmetrie in den Umkehrpunkten erkennt man schon in den Geschwindigkeiten und noch viel besser in den Beschleunigungen, die sogar eine zusätzliche Symmetrie aufweisen.
Beispiel 2: Parallaxe bei einer Kreisbewegung
Dieses Beispiel ist einfacher als das erste, da es hier nur um den Winkel beta im Falle eines festen Bezugspunktes geht.
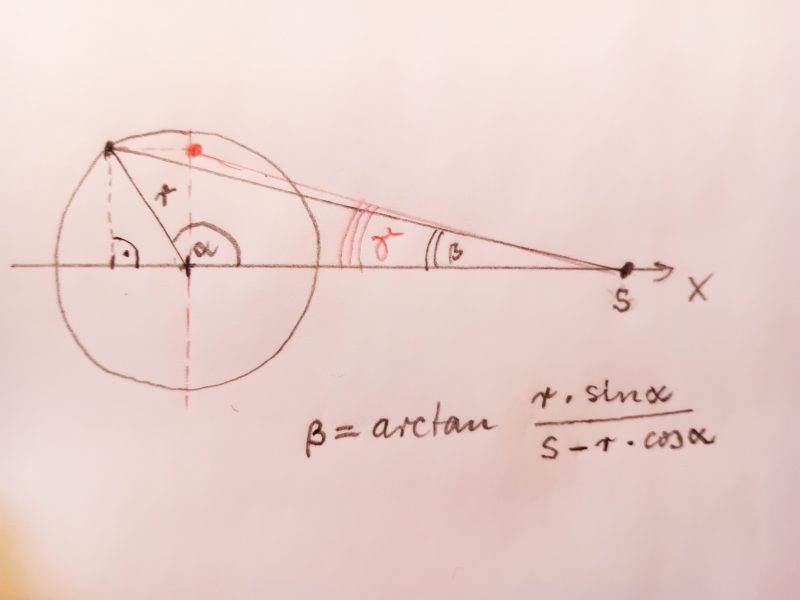
Handskizze zur Kreis-Parallaxe, rot für einen auf der y-Achse schwingenden Punkt
Der Zeitablauf sieht dann so aus:
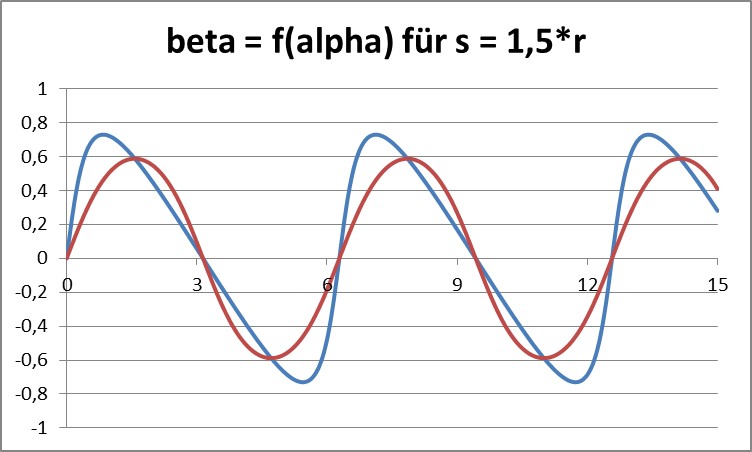
Blau ist die Kreis-Parallaxe, rot die auf einer Geraden
Man erkennt deutlich, dass die blaue Kurve erstens ihr Maximum schneller erreicht (Blickrichtung als Tangente an den Bewegungs-Kreis) und zweitens ein größeres Maximum hat (Tangentenpunkt ist dichter am Bezugspunkt, weshalb der Winkel beta größer werden kann!).
Für ein großes s gehen beide Kurven ineinander über, was zum Beispiel in der Astronomie für eine Parallaxe des Sirius, erzeugt durch die Beobachtung von der Erdbahn aus, zutreffen würde.
Beispiel 3: Marsschleife vor dem Fixsternhimmel (siehe dort!)
Hier bewegen sich nun Beobachter und Objekt beide, und zwar auf nichtebenengleichen Ellipsen unterschiedlicher Exzentrizität.
Kommentar abgeben