Näherungen und Näherungsmethoden, Abschätzungen, Schätzwerte, Überschlagsrechnung
(letzte Änderung: 28.08.2018)
Man hört oft von Physikern (und manchmal von Ingenieuren) den verschmitzten Satz:
„In nullter Näherung ist das soundso viel!“
Das impliziert, dass es auch erste, zweite und höhere Näherungen geben müsste. So ist es auch. Damit ist gemeint, dass es Näherungsverfahren gibt, die sich schrittweise an den „richtigen“ Wert heranpirschen, also „nähern“. Die „nullte Näherung“ ist dann eine Startwert-Annahme, die noch nicht auf einer Rechnung beruht, sondern geschätzt ist. „Nullte Näherung“ ist somit einfach eine Abschätzung aus Erfahrung oder durch „scharfes Hingucken„.
Entsteht das Erfordernis einer Näherung nun aus persönlicher Schwäche in Mathe oder woraus? Nein. Vielleicht hat man schon einmal von transzendenten Gleichungen gehört, die man also nicht nach der gesuchten Variablen umstellen kann und somit nicht zu lösen in der Lage ist?
Dann hilft nur das systematische Heranpirschen an die Lösung, was schriftlich sehr aufwendig ist und mit Hilfe der Rechentechnik ganz einfach wird.
Aber neben den mathematischen gibt es auch physikalische Gründe für schrittweises Nähern: Zuerst vernachlässigt man alle als nebensächlich betrachteten Einflüsse und kommt zur „Nullten Näherung“, bevor man schrittweise nach ihrer Rangfolge alle Nebeneffekte in die Berechnung einbezieht. Sowohl die mathematischen als auch die physikalischen Aspekte sollen hier an Beispielen angerissen werden.
Erstes Beispiel:
Wir machen mal zuerst ein ganz einfaches Beispiel zum Nachrechnen, das auch analytisch, also ohne Näherung, lösbar ist, und vergleichen dann die Ergebnisse:
Ich stoße eine Leichtathletik-Kugel, die so schwer ist, dass wir ihren Luftwiderstand vernachlässigen wollen (physikalischer Aspekt; Berücksichtigung des Luftwiderstandes ergäbe eine unsymmetrische Flugbahn, wie es mit der Wasserrakete durch nemerische Integration berechnet worden ist), waagerecht (schlampiger Weise, aber physikalisch wieder genähert!) von mir weg und will wissen, wie weit sie fliegt, bevor sie auf dem waagerecht gedachten Boden auftrifft.
Gegeben sind also die Abstoß-Höhe h und die waagerechte Geschwindigkeit vw (senkrechte Komponente der Geschwindigkeit vs0 ist Null). Gesucht ist die Flugweite sb, gemessen auf dem Boden. Wir dürfen Beschleunigung, Geschwindigkeit und Weg vektoriell zerlegen sowie zusammensetzen, so dass wir mit den Komponenten getrennt arbeiten dürfen.
Nach dem Fallgesetz wissen wir, dass die Kugel nach der Zeit tb auf dem Boden aufschlägt, wenn sie zur Startzeit to = 0 ruht und aus der Höhe h herabfällt:
tb = Wurzel(2*h/g) mit g als Fallbeschleunigung.
Dieser Zusammenhang ergibt sich aus der zweifachen Integration der Beschleunigung, der die Kugel in ihrer senkrechten Bewegung (Index s) unterliegt:
as = g as ist die senkrechte Beschleunigung
vs = g*t für vs0 = 0
h = g*t²/2 für ho = 0, daraus die obige Gleichung für t=tb
In der Zeit tb hat die Kugel waagerecht den Weg
sb = vw*tb = vw * Wurzel(2*h/g)
zurückgelegt und schlägt genau dort auf! Jetzt können wir in diese analytische Lösung die Zahlen einsetzen und erhalten das gesuchte Ergebnis.
Mal angenommen, wir wären zu doof zum Umstellen der Gleichung h =g*t²/2 nach t (wie oben geschehen), so müssen wir so lange mit t herumprobieren, bis für h die tatsächliche Abstoßhöhe herauskommt. Das geht nun wirklich nur mit Zahlen:
h soll 1,6 m sein, g nehmen wir der Einfachheit halber („ohne Beschränkung der Allgemeinheit“ der Näherungsmethode!) mit 10 m/s² an (mathematische Näherung).
„Nullte Näherung“, also Schätzwert, soll eine halbe Sekunde sein (physikalische Errfahrung mathematisch, also numerisch, umgesetzt).
„Erste Näherung“ ist dann das Ergebnis der ersten Korrektur nach Auswertung der Gleichung:
h = 10 m/s² * (1/2 s)²/2 = 10/8 m = 1,25 m
Das ist weniger als die Fallhöhe, die Zeit ist also zu kurz angesetzt. Wie nun weiter?
Ein simples „Intervall-Schachtelungs-Verfahren“ geht so, dass man ein Start-Intervall festlegt, um das man den Schätzwert korrigiert, neu rechnet, und dann entscheidet, ob man in gleicher Richtung das gleiche Intervall weiter geht oder in Gegenrichtung mit dem halben Intervall weiter macht. Sobald man so nah am richtigen Ergebnis ist, wie man es für erforderlich hält (wir wollen es auf 1 cm genau haben!), bricht man ab. (Dieser Algorithmus schreit geradezu nach Programmierung, oder?)
Wir entscheiden uns für das Intervall 0,1 s und rechnen nun mit 0,6 s:
h = 10 m/s² * (0,6 s)²/2 = 1,8 m
Das ist zu viel, also mit dem halben Imntervall, also mit 0,05 s, in der Gegenrichtung, also mit 0,55 s rechnen:
h = 10 m/s² * (0,55 s)²/2 = 1,5125 m
Das ist zu wenig, also 0,025 s drauf:
h = 10 m/s² * (0,575 s)²/2 = 1,653 m
Das ist zu viel, also 0,0125 s weg:
h = 10 m/s² * (0,5625 s)²/2 = 1,582 m
Das ist zu wenig, also 0,00625 s drauf:
h = 10 m/s² * (0,56875 s)²/2 = 1,617 m
Das ist zu viel, also 0,003125 s weg:
h = 10 m/s² * (0,56875 s)²/2 = 1,5997 m
Das ist weniger als 1 cm von der gewünschten Höhe weg, also hören wir endlich auf.
Mit den 0,56875 s = tb bestimmen wir nun die Flugweite der Kugel, wenn wir für die waagerechte Komponente der Geschwindigkeit vw einmal 8 m/s annehmen:
sb = vw*tb = 8 m/s * 0,56875 s = 4,53 m
Das ist nicht berühmt, aber man stößt ja, wenn man möglichst weit stoßen will, auch nicht waagerecht, sondern etwas schräg nach oben… (Wie schräg als optimaler Winkel, das wäre eine ganz neue Aufgabe!)
Was wäre denn nun die „analytische Lösung“ gewesen?
sb = vw*tb = vw * Wurzel(2*h/g) = 8 m/s * Wurzel(2*1,6m/(10m/s²)) = 4,53 m
Fazit: Die Intervall-Schachtelungs-Methode funktioniert!
(Eine schneller zum Ziel führende Mehode interpoliert entweder die Intervallgröße oder nutzt, wie beim Newton-Verfahren, den Anstieg der Funktion im Gebiet der Lösung. Beides ist ebenfalls leicht programmierbar.)
ACHTUNG: Die Schachtelung versagt, wenn der erste Schätzwert jenseits eines lokalen Extremwerts der Funktion liegt, insbesondere also bei Schwingungen. Man sollte also eine Plausibilitätsprüfung zusätzlich zu Rate ziehen!
Die soeben ausprobierte Methode ist ein Algorithmus, den jedes Tier beherrscht, denn es ist einfach ein systematisches „Trial and Error“. Ein Hund sucht den Schwerpunkt eines langen Stocks zum Beispiel, bis dieser sich leichter tragen lässt. Mit der Erfahrung sinkt die Zeit seines Suchens! Man macht das auch als Mensch sogar mit zwei Variablen ganz instinktiv richtig, wenn man zum Beispiel mit dem Mauszeiger in Google-Earth den Gipfel eines Hügels sucht, der nicht explizit ausgewiesen ist, indem man solange hin- und her- und rauf- und runterfährt, bis eine maximale Höhe angezeigt wird. Dazu merkt man sich die bisherige Maximalhöhe (und den dazugehörigen Ort!) und probiert und korrigiert den gemerkten Wert (und Ort!) so lange, bis kein höherer mehr auftritt.
Mathematisch haben wir das physikalisch stark genäherte Problem sehr gut genähert. Nun also der nächste physikalische Schritt: Unter Beibehaltung der Vernachlässigung des Luftwiderstands wollen wir den Winkel des Abstoßes berücksichtigen, ohne aber zu bedenken (also unter physikalischer Vernachlässigung!), dass es sich nach oben schwerer stößt als nach vorn (das kommt dann soäter!).
Bei gleicher Abstoß-Geschwindigkeit v0 = 8 m/s (also gleich dem obigen waagerechten vw!) gibt es jetzt von vornherein eine senkrechte und eine waagerechte Komponente der Geschwindigkeit, wenn der Winkel zur Horizontalen beta heißen soll:
vw0 = vw = v0 * cos(beta) (bleibt unverändert, da kein Luftwiderstand)
vs0 = v0 * sin(beta) (ändert sich durch die Erdbeschleunigung)
Die Zeit bis zum Aufprall auf dem Boden verändert sich nun durch eine andere „Anfangsbedingung“ bei der Integration der Bewegungsgleichung:
vs = vs0 + g*t (hier ist die positive Richtung nach unten gemeint, wenn man g positiv ansetzt; daraus folgt, dass der Winkel beta ebenfalls nach unten positiv, nach oben also negativ anzusetzen ist – was sich aber nur im Sinus bemerkbar macht, im Cosinus – „gerade Funktion“ – jeodch nicht!)
Integrieren wir diese Gleichung über die Zeit, erhalten wir mit h als Starthöhe die Funktion für den Weg:
s = so + vso * t + g/2 * t²
für so=o und s=h erhalten wir für t=tb (Zeitpunkt des Auftreffens auf dem Boden) eine quadratische Gleichung:
tb² + 2*vso/g * tb – 2*h/g = 0
mit den Lösungen
tb = – vso/g +- Wu(vso²/g² + 2*h/g) mit vso = v0*sin(beta) und beta<0, also vso<o
Man sieht, dass die beiden möglichen Zeit-Lösungen symmetrisch um den Zeitpunkt des Gipfelpunkt-Durchlaufs angeordnet sind, die Zeit mit der negativen Wurzel also in der Vergangenheit liegt und den Zeitpunkt beschreibt, an dem die Kugel von der Erde aus losgeschleudert gewesen sein müsste, um die von uns erzeugte Flugbahn zu erreichen. Uns interessiert aber die Zeit, wann sie nach dem Abstoß wieder auf der Erde ankommt, also die positive Wurzel.
Setzen wir alle Werte ein, ergibt das eine Funktion für beta
tb(beta) = – v0*sin(beta)/g + Wu(vo²sin²(beta)/g² + 2*h/g)
= -8m/s*sin(beta) + Wu(64m²/s²*sin²(beta)/(10m/s²)² + 3,2m/(10m/s²))
Die Stoß-Weite ergibt sich dann aus
sb = vw*tb = v0*cos(beta)*tb
= – v0*cos(beta) * (v0*sin(beta)/g + Wu(vo²sin²(beta)/g² + 2*h/g))
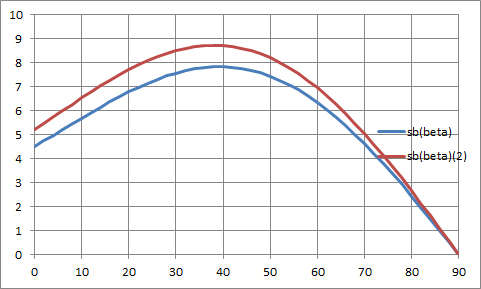
Für verschiedene beta ausgerechnet ergibt das dann folgenden Graphen für die Stoßweite sb als Funktion des Winkels beta ( hier nach oben gemessen) zwischen 0 und 90 ° (das ist NICHT die Bahnkurve, obwohl das fast so aussieht!!), und für senkrecht nach oben erfolgenden Stoß ergibt sich wirklich die Stoßweite Null:
Die Funktion ist nach beta differenzierbar (Produktregel beachten!), das Ergebnis gleich Null zu setzen und ergibt dann eine transzendente Gleichung, die man mit vielen Winkelfunktions-Theoremen umwandeln oder gleich mit dem Newtonverfahren näherungsweise lösen kann.
Hohe mathematische Genauigkeit erscheint aber noch nicht sinnvoll, wenn es physikalisch immer noch ungenau ist, weil wir mit konstanter Abstoß-Höhe (also unabhängig vom Abstoßwinkel, dabei zeigt unser Arm ja mit beta nach oben, wodurch der Abstoßort sich sowohl in der Höhe als auch in der Entfernung von der Stoßringkante ändert!)
Also weiter an das „echte“ Problem heranpirschen!
Wir brauchen nun unsere Armlänge la. Die nehmen wir mit 70 cm an, weil wir berücksichtigen, dass das Handgelenk etwas und die die Finger ebenfalls etwas angewinkelt sind. Dann verschiebt sich der Abstoß-Ort um dsw = la*cos(beta) nach vorn und um dss = -la*sin(beta) nach oben.
Berücksichtigen wir beides durch Korrektur in der Formel, so erhalten wir
tb(beta) = – v0*sin(beta)/g + Wu(vo²sin²(beta)/g² + 2*(h-la*sin(beta))/g)
und
sb =dsw+ vw*tb = la*cos(beta) + v0*cos(beta)*tb = (la + vo*tb)*cos(beta)
und einen neuen Graphen:
Als weitere physikalische Korrektur kann man berücksichtigen, dass die Abstoßgeschwindigkeit nachlässt, wenn eine senkrechte Komponente hinzukommt, weil man ja gegen die Schwerkraft arbeiten muss. Geht man davon aus, dass dem Arm (und natürlich den Beinen und dem Rumpf) nur ein bestimmtes Energiemaß für die Zeit des Stoßes zur Verfügung gestellt werden kann, so kann man die aufgebrachte potentielle Energie der Höhe von der kinetischen des waagerechten Stoßes abziehen (was natürlich wieder eine Näherung ist, denn die muskulären Körperfunktionen sind mit Sicherheit nicht so einfach linear, aber unter dem Gesichtspunkt des heuristischen Trainings von Näherungen physikalischer Art soll das hier stehen bleiben).
Die kinetische Energie der Kugel ist bei 9 m/s (nun kommt wohl die Masse hinzu?) für 7,25 kg
Wkin = m/2*v² = 7,25/2*64 Nm = 232 Nm
Gehen wir von einer linearen (sehr ideal!) gestalteten Angleit- und Abstoßkurve (oder für den Drehstoßer von einer echten Rotationsebene) unter dem Winkel beta aus, so ist die Höhendifferenz bei der gesamten horizontalen Bewegung (die oberhalb ja über den Stoßringdurchmesser hinausgehen darf) mit der Länge lmax maximal
dh = -lmax * sin(beta) = 2,50 m * sin(38°) = 1,54 m
und für die aufzubringende potentielle Energie
Wpot = m*g*h = 7,25*10*1,65 Nm = 112 Nm
etwa die Hälfte der kinetischen! (Um eine Relation wie „Hälfte“ herzustellen, benötigen wir die Masse nicht, denn die kürzt sich da raus…)
Da sträubt sich was in uns… Da sollen mal die Beinmuskeln (M. quadrizeps und andere) und Po- wie Rückenmuskeln richtig arbeiten und Tempo machen, damit der Arm dann nur den „Rest“ zu erledigen hat. Diese Muskeln müssen uns sowieso tragen, sollen sie sich nicht so haben.
Da wir hier aber das Nähern üben, tun wir mal so, als ob wir einen Akku hätten, der nur eine bestimmte Leistung (wegen bestimmter Widerstände) und somit in einer bestimmten Zeitspanne nur eine bestimmte Energie abzugeben bereit sei. Wie sähe unsere Winkelabhängigkeit dann aus?
Die kinetische Rest-Energie WkinR wäre dann (beta immer nach unten gezählt!)
WkinR = m/2*voreal² = Wkino – Wpot = m/2*vo² + m*g*lmax*sin(beta)
und daraus die reale Anfangsgeschwindigkeit
voreal = Wurzel(vo²+2*g*lmax*sin(beta))
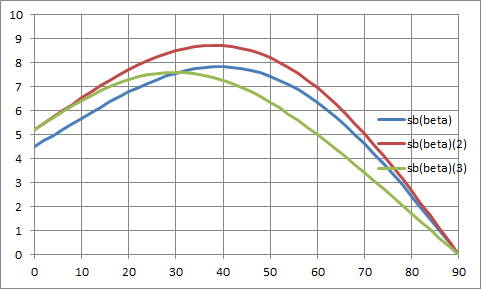
Arbeiten wir das in die obigen Formeln ein (das wird jetzt richtig Arbeit, oder man macht in EXCEL Zwischenrechnungsspalten für die Teilfunktionen), erhalten wir wieder einen neuen Graphen:
Wie zu erwarten, wird der Stoßer nun höhenbeschränkt und stößt flacher, was wir ja tatsächlich an uns selbst und an den Weltmeistern beobachten!! War diese biokinetisch motivierte (und im elektrischen Analogon beschriebene) Näherung also gar nicht so schlecht???
Naja, die Energie der Muskeln geht ja nicht nur in die Kugel, sondern auch in den zu bewegenden Körper selbst, denn der ist ja auch nicht masselos. Man müsste nun also seine Körperteile dahingehend untersuchen, welche sich an der Aufwärtsbewegung beteiligen müssen, welche erst nach vorn beschleunigt werden müssen und welche bei der Wirkung des Rückstoßes wieder abgefangen werden. Das ist ein biomechanisches Mammut-Vorhaben, weshalb es dafür ja auch Diplomarbeiten an der DHfK und anderswo gab und gibt…
Zweites Beispiel:
Ein schwerer (besser: ein geführter) Stab bewegt sich waagerecht auf eine am Faden ruhend aufgehängte deutlich leichtere Kugel (physikalische Näherung, um die Masse des Stabes als relativ unendlich – „groß gegen“ – ansehen zu können und die Kugel also an ihm „reflektieren“ zu lassen, das heißt die Änderung der Stabgeschwindigkeit mit Null festsetzen zu können) zu und stößt diese elastisch an, wobei der Stab seine Bewegung mit gleicher Geschwindigkeit fortsetzt. Die Kugel pendelt vom Stab weg und kommt dann schwingend zurück. Wann und wo trifft sie wieder auf den entgegen kommenden Stab?
Physikalisch genähert dürfen wir also mathematisch davon ausgehen, dass die Kugel direkt nach dem Stoß die doppelte Geschwindigkeit des Stabes hat, wenn der Stoß elastisch war.
Gesucht ist also (unter Vernachlässigung der physikalischen Werte und mit Anpassung der Konstanten an den Sinus) der Schnittpunkt der Sinuskurve (siehe auch Schwingung)
y1 = sin(t)
mit der Geraden
y2 = t/2
im positiven Bereich von t mit einer willkürlich angenommenen Genauigkeit von 0,001 (ein Promille der Amplitude).
Normalerweise ermittelt man Schnittpunkte über deren einfache Eigenschaft, dass beide Funktionswerte gleich sind, also durch Gleichsetzung:
sin(t) = t/2
Für das Newtonverfahren (es erfordert eine Differenzierbarkeit der Funktion) ist es einfacher, die Gleichung so umzustellen, dass man eine Nullstelle einer Funktion sucht:
y = sin(t) – t/2 = 0
Erste Ableitung:
y‘ = cos(t) – 1/2
Nullte-Näherungs-Schätzwert: t0=2
y0 = sin(2) – 2/2 = -0,0907
Nun arbeitet man so weiter, dass man am ermittelten Schätzpunkt des Funktionsgrafen eine Anstiegstangente anlegt und deren Schnittpunkt mit der t-Achse ermittelt und diesen als nächste Näherung der Nullstelle ansieht und dann diesen Vorgang so lange wiederholt, bis man die gewünschte Genauigkeit erreicht hat.
Mit dem allgemeinen Anstiegs-Dreieck y‘ = (y2-y1)/(t2-t1) erhält man für die iterativen alten (Index a) und neuen (Index n) Werte mit yn=0
tn = ta – ya / y’a
und also für die erste Rechnung
t1 = t0 – y0 / y’0 = 2 + 0,0907/(cos(2)-1/2) = 1,900996
Jetzt ist y1 = -0,00452 und im Betrag also noch etwas größer als 0,001.
t2 = t1 – y1 / y’1 = 1,895512
Schon im nächsten Schritt ergibt sich y2 = -1,4233 * 10 hoch -5 (Genauigkeit also locker erfüllt!) und
t3 = 1,895494
Das Newton-Verfahren ist also sehr schnell („konvergiert“ schnell), so dass man sogar in wenigen EXCEL-Zeilen zum Ergebnis kommt und nicht einmal wirklich „programmieren“ muss. Hier der Graf der Funktionen und die EXCEL-Tabelle zur Iteration des Schnittpunkts/Nulldurchgangs:
Ein „Programm“ (z.B. in VBA für EXCEL) würde also mit einer Schleife mit kopfgesteuerter Abbruchbedingung arbeiten.
Hier noch die grafische Veranschaulichung der Schritte durch kleine Pfeile sowohl für die Tangente als auch zum neuen Funktionswert, wenn man für die deutlichere Sichtbarkeit als Startwert die grobe Annahme 3 (statt 2) macht:
Drittes Beispiel: Überschlagsrechnung
Auch ohne das Newton-Verfahren ist die Kenntnis der ersten Ableitung einer Funktion oder die Kenntnis einer Reihenentwicklung nicht von Nachteil. Dann kann man mit ähnlicher Philosophie einer grafischen Dreiecksbildung einen recht guten Überschlag machen.
Schätze die Wurzel von 50 möglichst schnell und möglichst genau!
Ich kenne die Wurzel von 49, denn das ist 7. Ist das von Nutzen?
Mit der Umformung
50 = 49+1 = 49*(1+1/49)
habe ich zwei Faktoren gebildet, aus denen ich die Wurzel einzeln ziehen kann. Wichtig ist, dass einer der Faktoren dicht bei Eins liegt, damit man die Summe aus 1 und einer Zahl, die klein gegen 1 ist, für die Näherungen nutzen kann, für die unten eine kleine Tabelle angehängt ist.
Wurzel(49) = 7 und Wurzel(1+1/49) =etwa (1+1/98) ergibt sich durch Multiplikation
7*(1+1/98) = 7 + 7/98 = 7+1/14 =etwa 7,07.
Probe:
7,07² = 49,985 oder (7+1/14)² = 50,005
Beides ist hinreichend genau. Man hätte auch kürzer sagen können, dass 50 von 49 um etwa 1/50 = 2% abweicht und die Wurzel deshalb um etwa 1/100=1% abweichen muss, und das ergibt 7,07.
Hier die Tabelle (Argumente der Winkelfunktionen im Bogenmaß!):
Viertes Beispiel: Interpolation und Extrapolation
Unter Interpolation versteht man die Berechnung eines Wertes, der zwischen zwei bekannten Werten liegt. In erster Näherung interpoliert man linear, was bei linearen Funktionen natürlich schon genau ist. Man setzt eine Porportionalität von abhängiger und unabhängiger Variablen voraus und fertig.
Beispiel:
Nach 12 Minuten habe ich 20 Bäume markiert und nach 15 Minuten 26 Bäume. Wieviel Bäume habe ich nach 14 Minuten markiert? Das aktuelle Tempo ist (26-20)/(15-12) Bäume/Minute gleich 2 Bäume/Minute. (14-12) Minuten *2 Bäume/Minute sind 4 Bäume. Also habe ich (20 + 4) Bäume markiert.
Mathematisch habe ich also die Proportionen ähnlicher Dreiecke verwendet:
(yn-y1)/xn-x1) = (y2-y1)/(x2-x1)
Nach yn umgestellt ergibt sich der obige Gedankengang:
yn = y1 + (xn-x1) * (y2-y1)/(x2-x1)
(Übrigens ist die benutzte Proportionalität nicht wirklich global, denn die Funktion geht nicht durch den Nullpunkt der Zeit. Offenbar gab es zwei Minuten Rüstzeit oder ein Anpirschen an die später als konstant gedachte Arbeitsleistung.)
Will ich nichtlinear interpolieren, kommt zum Beispiel die quadratische Interpolation in Frage, für die ich aber eine Annahme über die Krümmung benötige. Diese kann ich aus drei gegebenen Punkten als Differenz der Differenzen ermitteln und somit einen unbekannten berechnen.
Liegt mein gesuchter Punkt außerhalb der bekannten Punkte, sprechen wir von Extrapolation.







Kommentar abgeben