0.3 Kristallsammlung
Dass hier eine Kristallsammlung und keine „Mineraliensammlung“ eingestellt wird, liegt am Thema der gesamten Seite, in der es um „Struktur“ geht. Kristalle und Achate sind die beiden Extrema der makroskopischen Mineralien-Struktur und somit auch extrem in ihren Erscheinungsformen für das menschliche Auge.
Die Hintergründe der Bildung von Kristallen sind in anderen Abschnitten behandelt worden. Hier geht es vor allem um typische Beispiele zu den anderen Behandlungen. Der Betrachter möge die Rückschlüsse selber ziehen und hier erst einmal einfach genießen.
Ein wenig Ordnung muss natürlich sein, und deshalb sind die wenigen ausgewählten Kristalle nach den Kristall-Systemen sortiert, und zwar in der Reihenfolge im Sinne des Abschnitts Kristallografie bei den naturwissenschaftlichen Grundlagen:
- kubisch
- hexagonal
- trigonal
- tetragonal
- rhombisch
- monoklin
- triklin
1. Einige Kristalle des kubischen Systems
Hierher gehören viele Metalle, Halogenide, Sulfide, Granate.
Der sehr formenreiche Pyrit (viele schon dargestellt im Abschnitt über die Trachten der Kristalle) und der Fluorit haben es mir besonders angetan, weil bei ihnen die „niedrig indizierten“ Flächen der einfachen Fasen von Kanten und Ecken häufig vorkommen und selten auch mit „höher indizierten“ kombiniert sind. („Millersche Indizes“ bitte extern recherchieren und studieren!) Der Fluorit kommt meist in Würfelform und selten in Oktaederform (obwohl das seine bevorzugte Form beim leicht zu bewerkstelligen Spalten ist!) vor, und nicht selten sind seine Würfelkanten durch die Dodekaederflächen (110) angefast. Im Osterzgebirge kennt man als Achat-Sammler vor allem seine großen Würfel-Negative von Reichstädt und seine derben blauen Schichten von Johnsbach sowie die gelben Kristalle um Holzhau. Im Mittleren Erzgebirge gibt es ihn in vielen Farben. Fluorit gibt es weltweit, so dass er allein ein Sammelgebiet für sich sein könnte. (Siehe „Terra Mineralia“ in Freiberg/Sa.!)
Hier nun ein paar Beispiele für charakteristische Fluorit-Kristalle:
Im zweiten Beispiel (Fernost) gibt es interessante Flächen an den Ecken:
Natürlich ist auch Kochsalz (NaCl) interessant:

Links: Riese aus Merkers mit kleinen Gruppen nahe der Flächenmitte; Rechts: Zu Hause gezüchtete Kristallgruppe mit Kleinwinkelkorngrenzen
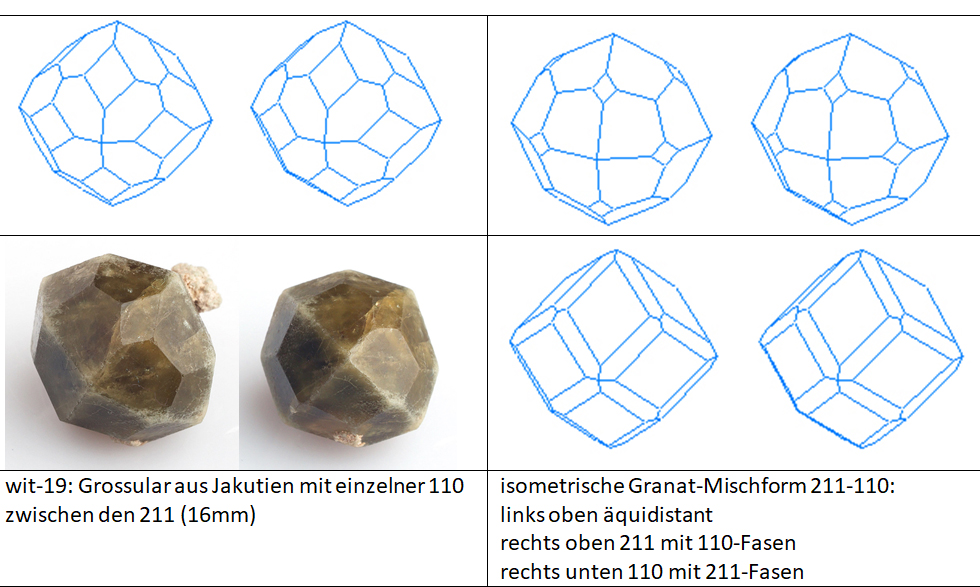
Die Granate (Inselsilikate mit 2- UND 3-wertigen Kationen) bilden oft Rhombendodekaeder oder sogar Drachenviereck-24-Flächner (Deltoid-Ikositetraeder):

Auch hier weicht die kristallografische (translationsinvariante) Form von der (Regelmäßige-n-Eck-) Idealform ab (wie beim Pyrit!).

Hier habe ich mal die Sauerstoffatome im Granat hinzugezeichnet und das Genze etwas gedreht, aber das verwirrt vielleicht nur…
Weitere schöne Granate:
(„YIG“ ist der englische Yttrium-Eisen-Granat, gezüchtet am Institut für Kristallografie in Moskau 1972)
Die Sulfide sind durch ihre metallisch glänzenden Oberflächen und variablen Trachten immer eine Augenweide:
Ein besonderer Kristall ist der des Tetraedrits:
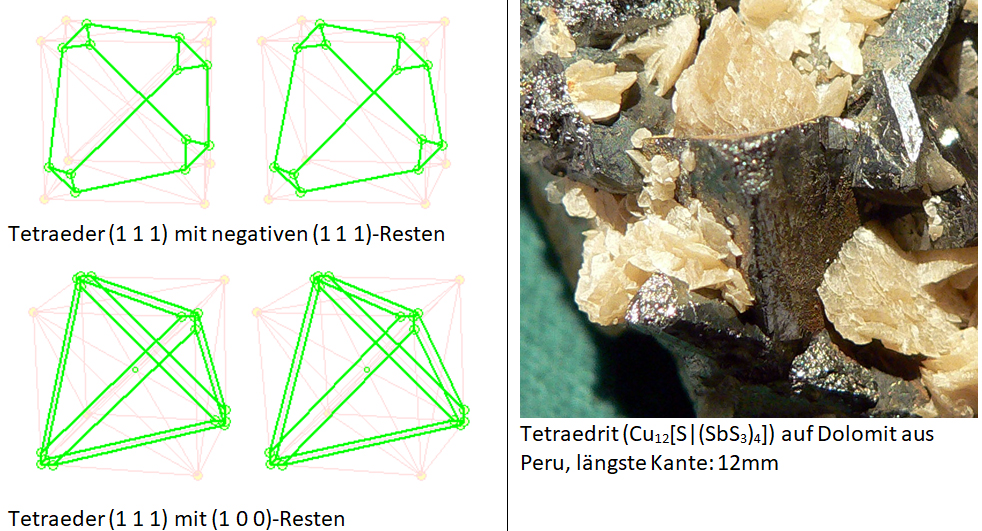
Der Tetraeder ist mit seinen scharfen Kanten und Ecken in der Mineralogie etwas besonders Seltenes, da er meist durch „negative“ Flächen ergänzt wird.
Ich nehme der Vollständigkeit halber auch mal die nicht im kubischen System kristallisierenden dazu, die tauchen dann an richtiger Stelle auch wieder auf:
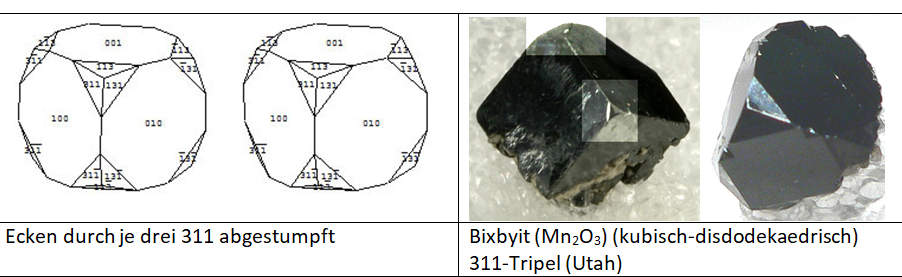
Und schließlich darf man die Oxide nicht vergessen. Die Oxide mit gemischtwertigen Kationen sind dabei die verrücktesten:
Auch die Elemente können Spaß machen, wenn sie nebenbei auch als Drähte, Bleche oder andere Gebilde auftreten:
2. Einige Kristalle des hexagonalen Systems
Hier sind die Berylle als Edelsteine besonders begehrt. Für den Einkristallsammler unterscheiden sie sich insbesondere durch die Kopf-Gestaltung der hexagonalen Säulen. Hier können Ecken und Kanten mehrfach abgefast sein.
3. Einige Kristalle des trigonalen Systems
Die Spitzenreiter der Formenvielfalt sind hier Calcit (ditrigonal-skalenoedrisch) und Quarz (trigonal-trapezoedrisch). Damit könnte man sehr viele Seiten füllen, man muss sich also stark beschränken. Beginnen wir mit den schönsten Quarz-Kristallen, den Schweizer Rauchquarzen aus dem Val Giuv (tw. alte „klassische“ Flächenbezeichnungen benutzt):
Bei meinem Besuch im Tal war Nebel und Nieselregen… Zum Glück gibt es Leute, die von ihren Funden etwas abzugeben bereit sind! (Die schönen Amethyste aus dem Osterzgebirge sieht man mit bei den Achaten.)
Die Calcite haben nun ganz viele Varianten der Kopfgestaltung (unterschiedlich steil), so dass sie durch ihre ditrigonal-skalenoedrische Klasse die größte Vielfalt aller Mineralien bilden können. Da muss man sich noch viel weiter einschränken: Hier sollen nur die seltenen isometrischen Formen und die noch selteneren flachen Kopf-Ausprägungen sowie die „Kugel“ und Zwillinge gezeigt werden (daneben natürlich auch die Doppelspat-Grundform, aber die berühmten Fundstellen von der britischen Insel fehlen hier!):
4. Beispiel aus dem tetragonalen System
Am bekanntesten sind wohl die Rutil-Nadeln im Quarz, die als „Feenhaar“-Steine gern zu Schmuck verarbeitet werden. Außerhalb des schützenden „Wirts“ (der erst später gewachsen sein kann!) wirken sie sehr zerbrechlich und sind es auch:

Im Internet – nicht bei mir! – schweineteuer (weil sehr selten) zu haben: Ring mit komplettem Sechser
5. Beispiele aus dem orthorhombischen System
Besonders häufig ist im gesamten Osterzgebirge der Schwerspat (Baryt). Er kommt als derbe Masse (auch schön gebändert, siehe in Reichstädt zum Beispiel), Blätterspat in Gängen und manchmal auch schön ausgebildet in Drusen (im Flussspat von Johnsbach oder im Amethyst von Schlottwitz oder direkt im Muttergestein von Holzhau und anderswo) vor. Sehr spannend sind auch die damit ebenfalls häufigen Pseudo- und Perimorphosen des Quarzes (Amethyst!) nach Baryt im Osterzgebirge.
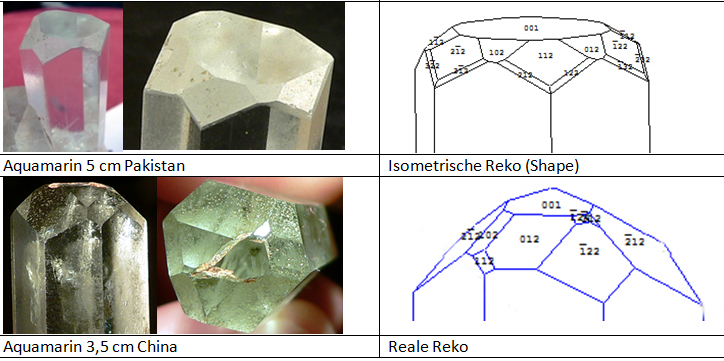
Da im Osterzgebirge im Altenberger Pyknit Stengel-Topas (vielfach senkrecht zur Stengel-Achse gebrochen) und weiter westlich am Schneckenstein heller gelblicher Topas (in schönen Einzelkristallen zwischen Quarz) auftritt, soll dieser hier auch behandelt werden. Die orthorhombisch-dipyramidale Klasse lässt ebenfalls viele Kopfformen und außerdem viele Mantelflächen zu, was den die Flächenvielfalt suchenden Kristallsammler natürlich reizt.
An dem oben abgebildetetn Pakistaner will ich einmal zeigen, was das auch für Arbeit macht, alle „Formen“ (Flächen-Typen) zu ermitteln. Die Messung der Kantenwinkel ergab interessante Werte, deren kristallografische Berechnung sehr lange gedauert hat, weil mir ein peinlicher Fehler unterlaufen ist: Ich habe die Deckfläche mit (100) statt mit (001) bezeichnet, was im kubischen System keine Rolle gespielt hätte, im orthorhombischen (orthorhombisch-dipyramidal) aber tödlich ist.
Die Deckfläche selber zu finden gelang unter der Annahme, dass es wahrscheinlich parallele Kanten zwischen den Mantelflächen (alle gehören zur Zone der Deckflächennormalen) gibt. Aber schon die Untersuchung der Winkel zwischen den Mantelflächen war irritierend, weil kein rechter darunter war, auch nicht, wenn man mehrere Winkel beliebig addierte. Gegenüberliegende parallele Flächen waren aber zu finden. Daraus folgt, dass die Mantelflächen alle nicht EZ-parallel sind, also nicht zum Basisprisma gehören können.
Die auftretenden parallelseitigen Fasen der Kopfflächen weisen auf weitere Zonen hin, so dass man durch rechnerisches Probieren mit den niedrigsten Indizes relativ schnell zur Lösung kommt.
Gefunden wurden 12 echte Formen (in Tabelle unten fett).
Man könnte auch „unechte“ hinzufügen, da die Kantenwinkel der Fasen untereinander und zur Kopffläche von der Bezugsachse (a oder b) abhängen.
Benutzte Daten in Shape und Adolphi: a = 4,65 Å; b = 8,80 Å; c = 8,39 Å (Wiki).
| Kante | gemessen (Anlege-Goniometer) | berechnet
Shape |
berechnet
Ad EXCEL |
| Mantel (4 Formen) | |||
| 110–120 | 19 | 18,7 | 18,7 |
| 120-130 | 14 | 11,2 | 11,2 |
| 110-340 | 08 | 07,3 | 07,3 |
| 340-120 | 10 | 11,4 | 11,4 |
| 110-110 | 56 | 55,7 | 55,7 |
| 120-120 | 88 | 86,8 | 86,8 |
| 120-130 | 76 | 75,7 | 75,7 |
| 120-110 | 19 | 18,7 | 18,7 |
| Kopf (6 Fasen-Formen) | fette Summe = 180 ok | ||
| 001–011 | 43 | 43,6 | 43,6 |
| 001-021 | 65 | 62,3 | 62,3 |
| 001-101 | 61 | 61,0 | 61,0 |
| 001-103 | 32 | 31,0 | 31,0 |
| 001-113 | 35 | 34,2 | 34,2 |
| 001-112 | 45 | 45,6 | 45,6 |
| 001-111 | 61 | 63,9 | 63,9 |
(Das Flächenberechnungsprogramm Adolphi in EXCEL funktioniert offenbar problemlos! Deshalb unten keine weiteren Gegenüberstellungen der berechneten Winkel.)
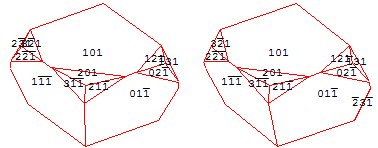
Hier die schrittweise Rekonstruktion geometrisch:
(Hier ist auf Stereo-Bilder verzichtet worden.)
Hier zwei eitere orthorhombisch kristallisierende Mineralien:
Und hier noch ein Beispiel des Nachbaus eines Plexiglas-Kristall-Modells mit „Shape“ für Robert Sweredjuk (siehe Kommentar):
6. Einige Kristalle des monoklinen Systems
Die häufigsten Vertreter sind sicher Gips und Orthoklas (ein Feldspat). Beide fallen dann besonders auf, wenn sie Zwillinge bilden, weil diese einspringende Winkel haben können, also zum Beispiel „Schwalbenschwänze“ bilden. Die Analyse von Zwillingen ist noch spannender, vor allem dann, wenn man noch nicht weiß, nach welchem Gesetz sie gebildet worden sind. Gips kann (im Südharz zum Beispiel) schön stengelig ausblühen oder auch als durchsichtige Tafelen („Marienglas“) vorkommen. Die „Rosen“ (grünlich im Nordwesten von Halle/S. oder orange aus der Wüste Nordafrikas) bilden sich in lockerer Umgebung aus und zeigen oft Einschlüsse von dieser.
Hier ein Orthoklas-Zwilling („Manebacher“) aus dem Vogtland von der namensgebenden Stelle:
Und weitere Vertreter:
Kandiszucker ist monoklin-sphenoidisch und bildet manchmal schöne Kristalle in klaren Gelees, wie zum Beispiel in meinem „Löwenzahnhonig“ in herrlichem Goldgelb. Es entsteht ein interessantes technologisches Dilemma, wenn man diese scharfkantigen Exemplare aus der klebrigen Masse befreien will:
- man lässt den Gelee-Rest antrocknen oder versucht ihn abzuwischen, dann sieht man die ursprüngliche Kristalloberfläche unter den verbleibenden Resten nicht mehr
- man leckt (oder spült) den Gelle-Rest ab, dann rundet man durch Anlösen die Kristallkanten und rauht nebenbei auch die Flächen auf
7. Beispiele aus dem triklinen System
Auch hierher gehören einige Feldspate. Am bekanntesten ist aber sicher das Kupfersulfat-Pentahydrat (CuSO4 · 5 H2O), mit dam man in der Schule schöne blaue Kristalle gezogen hat. Man konnte sich dannmanchmal an den schiefen Prismen („Parallelepiped“, aber dieser Begriff trifft auch auf andere Systeme zu!) erfreuen, wenn das Wachstum langsam genug erfolgt ist.























































Kommentare
Robert Sweredjuk am Samstag, 6. August 2022:
Guten Tag Herr Adolphi,
mein Name ist Robert Sweredjuk und ich hoffe sehr, Sie können mir bei der Identifizierung zweier Mineralien helfen!
Ich besitze etwa 40 Plexiglasmodelle aus den 1960er Jahren, die alle verschiedene Kristallformen darstellen,
insb. von Mineralien, wie z.B. Albit, Augit, Gips, Calcit usw..
Bislang konnte ich bis auf 2 Modelle alle identifizieren.
Jetzt meine Frage bzw. meine Bitte: Wäre es möglich, dass ich Ihnen von den beiden Modellen Fotos zusende und Sie mir bei der Identifizierung helfen könnten?
Über eine positive Antwort würde ich mich sehr freuen!
Vielen Dank
Und viele Grüsse
Ihr Robert Sweredjuk
Joachim Adolphi am Montag, 22. August 2022:
Lieber Robert,
gern sehe ich mir die Modelle an. Oft sind verzerrte Formen nur anhand der Winkel zu identifizieren. Bin gespannt.
Vielen Dank für die Anfrage!
J.A.
Joachim Adolphi am Montag, 22. August 2022:
Danke, Robert, für die Fotos, jetzt ist der Nachbau gelungen: Orthorhombisch. Das Stereo-Bild ist mit Indizes versehen. Das könnte Schwefel sein, Coelestin, Topas und weitere…
Ich habe die Bilder obern ergänzt…
LG JA
Milan M. am Samstag, 29. April 2023:
Guten Tag Herr Adolphi,
bei dem Bild 16 muss etwas durcheinander geraten sein. Diese Granate können meiner Meinung nach nicht von der Oelsener Höhe stammen. Die Granate der Oelsener Höhe sind eigentlich immer rissig. Und befinden sich in einem Glimmerschiefer.
Mit freundlichen Grüßen
Milan M.
Joachim Adolphi am Samstag, 29. April 2023:
Danke, Milan,
für den Hinweis; die Granate habe ich gekauft und dem Zettel geglaubt, ohne je dort selber gesammelt zu haben. Eigene Granate habe ich vor allem aus dem Vogtland und aus dem Granit des Rila-Gebirges (isometrische Winzlinge).
LG JA