4.2.3 Didaktische Nutzung der Geometrie für abstrakte Zusammenhänge
(letzte Änderung5..06.2020)
Viele Zusammenhänge lassen sich grafisch darstellen und erreichen eine ganz besondere „Schönheit“. Natürlich liegt diese – wie immer – im Auge des Betrachters: Ein gebildetes Auge sieht mehr!
Wenn man dafür einen Sinn hat, stellt sich die Frage auch manchmal umgekehrt: Welcher Zusammenhang steckt eigentlich hinter dieser Schönheit?
Ein auf solche Weise erregtes Interesse lässt oft eine Hartnäckigkeit bei der Suche nach der Lösung folgen, die ein Coach nie eintrichtern könnte.
Beispiel 1:
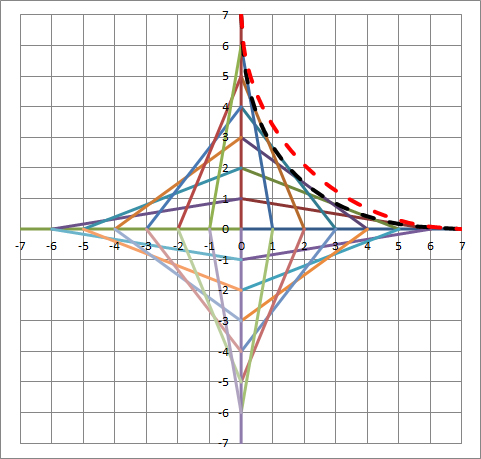
Mein Enkel Juri hat uns vor Jahren eine geometrische Zeichnung geschenkt:
Das kann man nachbilden:
Man erkennt das erzeugende Verfahren schnell:
- Die ganzzahligen Achsabschnitte werden paarweise so miteinander verbunden, dass sie je Quadrant die gleiche Summe bilden (hier 7).
- Beim Ausmalen entsteht ein räumlicher Eindruck, man meint den Mittelpunkt auf sich zukommen zu sehen.
Das Gebilde wirkt sehr harmonisch und hat etwas von einer „Minimalfläche“ an sich. Es ergibt sich für den geneigten Betrachter die Frage:
- Wie lautet der analytische Ausdruck für die „Einhüllende“? Was ist das für eine schön gebogene Linie im zweidimensionalen Fall (Fläche im dreidimensionalen)?
Man vermutet auf den ersten Blick, dass es sich um eine verschobene Hyperbel handeln könne, stellt aber nach kurzer Überlegung fest, dass hier in den Spitzen eine Tangente vorliegen muss, die parallel zu den Achsen ist. Außerdem muss die analytische Funktion symmetrisch in x und y sein, was auf eine binomiale Darstellungsmöglichkeit hinweist.
Physikalisch könnte man sie als „schienengebundene Schleppkurve“ erzeugen. Das ziehende Ende bewegt sich auf der x-Achse von 0 bis 7 und schleppt dabei das gezogene Ende von y=7 bis y=0. Aber HALT! Die Länge der Schleppstange ändert sich ständig, so geht das nicht:
Wenn also einzelne gleichzeitig erfolgende Roboter-Schritte senkrecht zueinander ein Kabel erforden sollten, könnte man hier über dessen Verlegung oder Elastizität nachforschen.
Gut. Also nun zur Mathematik. Jede einzelne erzeugende Gerade hat die Form
 |
c ist hierbei die feste Länge der Sternspitzen und a die variable Entfernung der Endpunkte der Geraden von Spitze bzw. Ursprung. Die Achsenschnitte sind (c-a) und a und ergeben zusammen auftragsgemäß c-a+a = c. Der Anstieg der Geraden ist dann im ersten Quadranten als Quotient der Achsschnitte negativ:
dy/dx = -(c-a)/a.
Die paarweisen Schnittpunkte der obigen 8 Geraden sind durch paarweise Gleichsetzung ihrer Gleichungen zu finden, wobei man möglichst einmal eine Differenz von 1 nehmen sollte und dann einmal dicht nebeneinander liegende Werte nehmen sollte, um der Handzeichnung von Juri nahe zu kommen und zu testen, ob die Werte stabil symmetrisch sind (der Einfachheit halber jetzt mit a und b oder ihrer Differenz d bezeichnet):
Das hat also geklappt. Aber wie kommt man nun zu einer analytischen Formulierung?
Wir probieren es so, dass wir b über a und d (b=a+d) ausdrücken und dann d gegen Null gehen lassen, wobei yn die Nachbargerade zu y sein soll:
Mit den beiden Gleichungen für ys und xs haben wir eine Darstellung über den „Parameter“ a. Gelingt es, nach diesem umzustellen, können wir aus beiden Gleichungen eine Funktion y(x) machen:
(Achtung: Hier muss man sehr sorgfältig alle Schritte nachrechnen, weil das c sowohl vor der Wurzel als auch innerhalb vorkommen kann!)
Mit dieser Funktion erhalten wir tatsächlich die richtigen Werte, prima.
Aber: Die eigenartige Funktion ys(xs) sieht nicht auf den ersten Blick so symmetrisch in x und y aus, wie wir das erwartet haben. Das muss man also prüfen! Dazu gibt es verschiedene Möglichkeiten:
Jetzt fragt es sich, wie weit diese Hüllkurve von einem Kreis (rot gestrichelte Kurve!) abweicht, denn dessen Gleichung sieht ja so ähnlich aus:
Der kleine symmetrische Zusatzterm -2xy macht den Unterschied!
Fazit: Es gibt etwas zwischen Kreis und Hyperbel, das ebenso ästhetisch ist!
Beispiel 2:
Wickelt man von einer feststehenden Rolle einen Faden (oder besser ein Blech?) ab, an dessen Ende man einen Stift befestigt ab und zeichnet auf einer Unterlage bei straffem Faden die Spur mit, so sollte am Anfang eine Kurve wie eine Zyklozykloide (Start senkrecht zur Rolle) und dann eine lieare Spirale (fast konstanter Abstand zwischen den Windungen) entstehen. Der Übergang sollte unmerklich stattfinden. Das könnte ästhetisch aussehen.
Also machen wir den Test!
Zuerst nehmen wir vereinfachend an, dass sich der Radius der Garnrolle durch das Abwickeln nicht ändert. Dann aber lassen wir (besser durch einen dünnen Blechstreifen) den Radius langsam kleiner werden, je Umdrehung um den gleichen Betrag.
Zuerst (durchgezogene Linien) sind die Formeln recht einfach, wenn wir den Rollenmittelpunkt in den Ursprung legen, bei der positiven x-Achse (Winkel phi=0) links herum beginnen und das Ende des Fadens als vektorielle Addition (also für jede Komponente getrennt) von Tangenten-Punkt des Fadens (im Radius r) und abgewickelter Fadenlänge s = r*phi in Tangentenrichtung beschreiben:
x(phi)=r*cos(phi) + r*phi*sin(phi)
y(phi)=r*sin(phi) – r*phi*cos(phi)
Lassen wir den Radius geringer werden (gestrichelte Linien), so ist dieser eine Funktion von s und s selbst eine Funktion von r und phi und damit auch wieder von s. (Das kann man differentiell abfangen: Methode der finiten Differenzen als numerische Integration! Bitte nachlesen und selber zum Beispiel in EXCEL probieren!)
Das Ergebnis sind tatsächlich schöne Kurven: Fadenende außen mit einer gemischten Kurve aus Zykloide und Spirale (könnte man auch einfach als spezielle „nichtlineare Spirale“ benennen) und innen die Kurve des sich verkleinernden Radius. Zum Vergleich ist schließlich noch der Versuch gemacht worden, einen auf der x-Achse verschobenen Kreis (grün) als Spiralen-Näherung für eine halbe Runde anzupassen:
Der Zoom in das Bild (Vergrößerung des Rollenradiusses) soll die unterschiedlichen Teile (außen, Übergang und Start) der Mischkurve zeigen.
Im übrigen ist das auch eine gute Übung der Umsetzung eines in Polarkoordinaten gedachten Ansatzes in eine kartesische Darstellung. Und? Lust zum Nachmachen?
Beispiel 3:
Wir wollen „schöne“ Kurven (Objekte) mit NUR einer Symmetrieachse herstellen. Kann uns das mit einfachen Mitteln gelingen?
Was bedeutet das mathematisch? Wenn die Symmetrie-Achse die y-Achse sein soll, brauchen wir eine symmetrische Funktion in x („gerade“ auf mathematisch, also geradzahlige Exponenten in der Taylor-Entwicklung). In y-Richtung nehmen wir also einfach ungerade Funktionen.
Kann man das getrennt ansetzen? Ja, wenn man eine Parameter-Darstellung wählt, also zwei Funktionen y(t) und x(t) gegeneinander als x-y-Plot von Punkten mit gemeinsamen t darstellt.
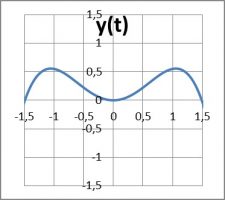
Einfacher Ansatz, der jeweils „Schlaufen“ enthält, weil es mehrere Nullstellen gibt, wäre
x(t) = d * t³ – e * t
y(t) = f * t4 – g * t²
Für d,e,f,g = 1,00; 0,75; -1,00; -1,00 ergibt sich folgendes Bild für -1 < t < +1:
Die Brezel entspricht genau unseren Symmetrievorstellungen. Verändert man die Parameter, ergeben sich andere „schöne“ Bilder:
Für d,e,f,g = 0,45; 1,00; -0,45; -1,00 ergibt sich folgendes Bild für -1,65 < t < +1,65:
Jetzt ist es eine Schleife, weil der Schnittpunkt der beiden Enden genau auf der Schlaufe liegt.
Letzte Spielerei mit diesem Ansatz:
Für d,e,f,g = 1,00; 0,50; -1,00; -1,00 ergibt sich folgendes Bild für -1,00 < t < +1,00:
Nun haben wir ein „Auge“ produziert!
Als Gleichung für eine Funktion f(x,y) gehört dazu folgender Ansatz, der den Schnitt der Oberfläche f(x,y) mit der x-y-Ebene darstellt:
f(x,y) = a * x4 – b*x²y +c* y³ = 0
Die Fläche f(x,y) sieht für a,b,c = 0,50; 1,10; 1,00 so aus:
Ihre Schnittlinie mit der x-y-Ebene ist der Übergang von Rot zu Grün. Numerisch ermittelt man dafür Werte, die als x-y-Plot so aussehen:
Man erkennt sehr gut den Zusammenhang mit den Bildern davor.
Für unsere Psyche heißt das:
Stetige Kurven mit einfachen Parametersätzen, die auch stetige Krümmungsänderungen enthalten, werden von uns als sehr elegante Erscheinungen gewertet. Sie bestätigen die instinktive Erwartung von „Masse-Trägheit“ und „elastischer Kraft“ im Zusammenhang von Körperbewegungen, die durch den Alltag immerzu verstärkend bestätigt wird.










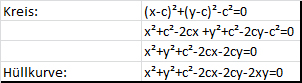













Kommentar abgeben