1.7 Trajektorien in diskreten Universen
Auch in diskret aufgeteilten („gerasterten“) Räumen kann man die Frage nach einer Trajektorie stellen, die selbst wieder diskret („gerastert“) oder auch stetig verlaufen oder etwaigen Bedingungen gemäß optimiert werden kann. (Vergleiche auch stetige Trajektorien in stetigen Universen im Punkt 2.8 mit seinen zahlreichen Unterpunkten oder das stetige Optimierungs-Beispiel 3.3 (Ski-Riesenslalom-Optimierung mit diskreten Torstangen) in den Extremwertaufgaben (in den „Grundlagen“ versteckte Variationsaufgabe!))
Ein einfaches zweidimensionales Beispiel, das der Veranschaulichung der Fragestellung dienen kann, ist ein quadratisches Raster, dem per Zufallsgenerator einige Hindernisse („Fallgruben“?!) bei ebenfalls zufällig gewählten Startpositionen am linken Rand eingefügt werden, die von den „frei programmierbaren“ Automaten beim Weg von links nach rechts so zu umfahren sind, dass es zumindest keine Zusammenstöße mit den Hindernissen gibt und eventuell auch zusätzlich ein minimaler Fahrtaufwand entsteht. Die Frage zielt also auf Algorithmen, die zur erfolgreichen Fahrspur („Trajektorie“) führen können.
Das lässt sich mit relativ einfachen Programmchen beginnen und führt schließlich zu den kompolexen Paketen fürs „Autonome Fahren“.
Hier geht es nur um die ganz einfachen Überlegungen zum heuristischen Start in diese Welt der bewegten Automaten („Fahr-Roboter“).
Die allererste Frage ist die nach dem Aufwand, den man jeweils treiben will, nämlich bezüglich der Sensoren, der Speicher und der Software:
a) einfache Sensoren, einfache Software, keine oder einfache Speicher:
Leicht aufzubauen, aber Gefahr von Sackgassen-Fallen, Mehrfachwegen und systematischem Abdriften (dafür aber: leichte Fehlersuche!)
b) komplexe Sensoren, komplexe Software, große Speicher:
Zeitaufwendige Programmierung, komplizierte Fehlersuche
Man kann das im Selbstexperiment – schrittweise komplexer werdend! – mit „Trial and Error“ erforschen und hat eine riesige Menge Spaß und AHA-Effekte dabei.
Fallgruben-Raster einfach
Unterwegs-Situation
Ziel erreicht
Fallgruben-Raster komplex (Stufe 4)
Das (gelbe) Fahrzeug soll von einer zufälligen Position am linken Rand zum rechten Rand gelangen, ohne in eine Fallgrube eines zufällig erzeugten Musters zu geraten und ohne das Spielfeld seitlich zu verlassen. Dazu wird es mit Nachbarschafts-Sensoren bestimmter Reichweite und Richtung ausgestattet und mit einem Entscheidungsbaum versehen. Später kann es auch noch mit einem Gedächtnis ausgestattet werden…
Es wäre schön, auch die Fahr-„Spur“ einzuzeichnen und somit das Ergebnis nicht nur durch die Zahl der benötigten Schritte (Tabelle rechts oben) anzugeben:
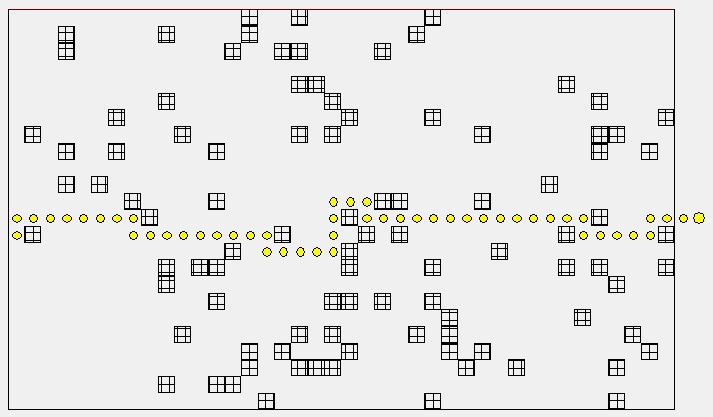
Hier ist nun schon die Erkennung und Vermeidung von einfachen Sackgassen eingebaut (Bildmitte) und das Ausweichen vor einfachen Fallgruben dem Zufall überlassen. (Stufe 3)
Dass der Zufallsgenerator auch Nachteile hat, sieht man an der folgenden Schrittzahl, die zeigt, dass das Programm den Roboter vor der Sackgasse mehrfach zappeln lassen hat.
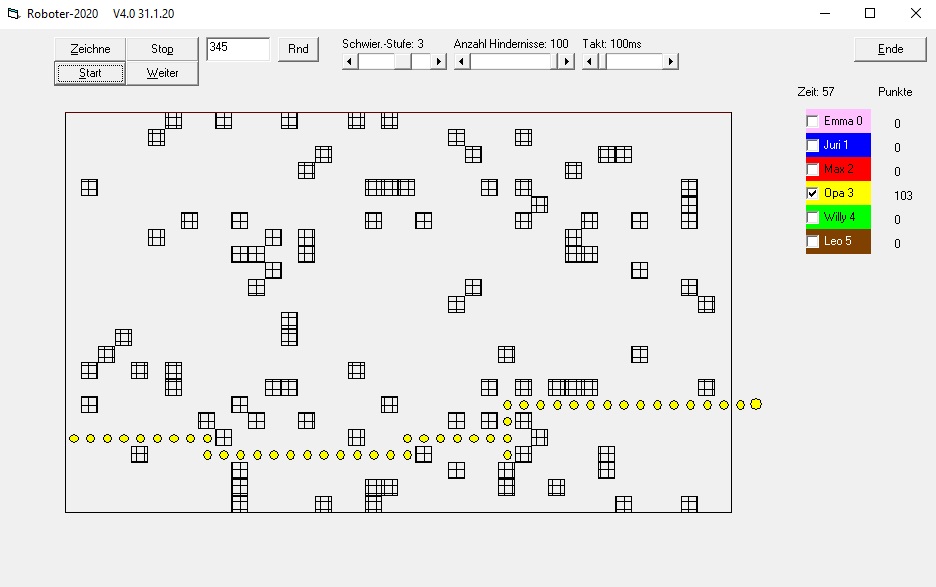
Statt der zu erwartenden knapp 50 Schritte sind es nun über hundert geworden, weil sich vor der Sackgasse mehrere Positionen mit zufälliger Richtungsauswahl beeinflusst haben. Hier wäre ein „Gedächtnis“ für den Roboter sinnvoll!
Ein vergleich unterschiedlich „gut“ programmierter Roboter erschließt sich aus folgender Spurenlage:
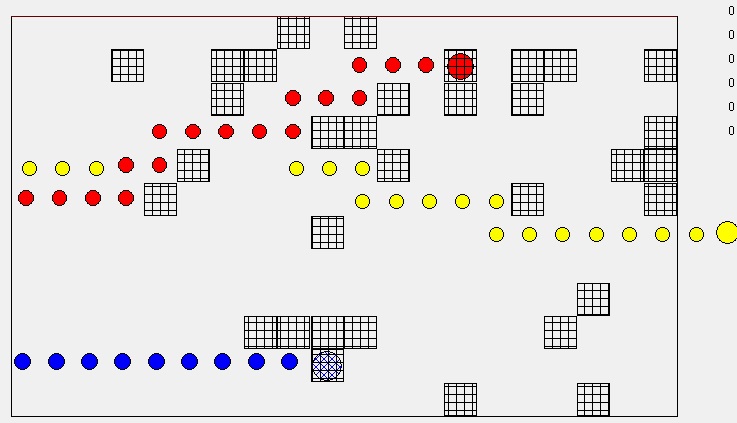
Blau: Ohne Ausweichen (erste Falle schnappt zu); Rot: Nur bei einer singulären Frontzelle Ausweichen (bei Pärchen quer schnappt Falle zu); Gelb: komplexere Ausweich-Strategie, hier aber zufällig nicht erforderlich
Auf dem gelben „Kurs“ wäre Rot zweimal in die „Falle“ zweier Frontalzellen getappt…
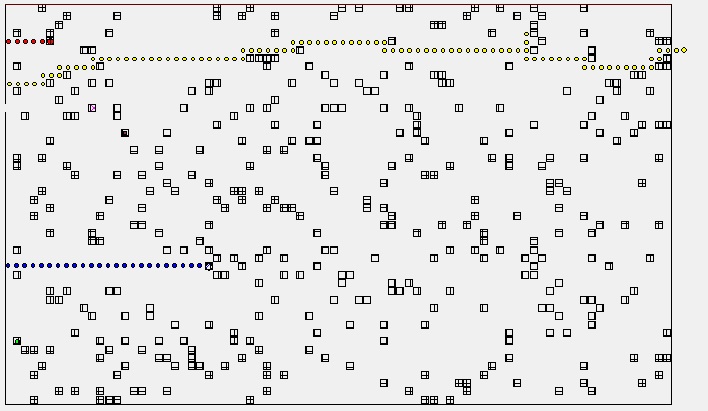
Auch in der höchsten Stufe konnte der Zufall rechts oben nach einiger Zeit bei der Auflösung helfen.
Mit allen 6 Teilnehmern sieht es dann so aus:
Das gegenseitige Überschreiben der Spuren muss noch irgendwie gelöst werden…
Grundsätzliche Unterscheidung bei der Konstruktions-Verbesserung:
- Erhöhung der Sensorreichweite erfordert die Berücksichtigung einer quadratisch wachsenden Zellenzahl und damit potenziell wachsende Entscheidungsbäume und/oder linear wachsende Vergangenheitsspeicherung (damit aber Varaintenreduzierung)
- sensorfrei informell komplette Feldkenntnis verlangt dafür Strategie-Algorithmus zur Auswahl der kürzesten Strecke
- Berücksichtigung anderer Roboter verlangt entweder zusätzliche Sensoren oder generellen Datenaustausch
Das Spiel mit den Strategie-Algorithmen ist ein höchst lehrreiches und jedem zu empfehlen!
Kommentar abgeben