4.3.1.3 Musik-Strukturelement 3: Klang-„Farbe“ und Instrumentalisierung
Kann man herauskriegen, warum die Instrumente unterschiedlich klingen, obwohl für alle grundsätzlich die gleiche Schwingungsgleichung gilt? Kann man die „Klang-Farbe“ selber ausrechnen??
Wie wir in den Grundlagen gelesen haben, ist die Verteilung der Schwingungs-Energie auf die Obertöne von der Konstruktion des Schwingers abhängig (damit ändert sich die Wellengleichung samt ihrer Randbedingungen…). Deshalb hat jedes Instrument seine Klang-„Farbe“, an dem wir es wieder-erkennen können. (Vergleiche grundlegende Überlegungen zu Saiten, Luftsäulen und schwingenden Plättchen/Stäben unter 2.4.1.1.2 „Elastische Schwingungen und Wellen im Stab“ und seinen Unterpunkten, besonders 2.4.1.1.2.5)
Dieses zusätzliche Strukturelement steht nur zur Verfügung, wenn wir es uns leisten können, so viele Instrumente zu besitzen, oder wenn wir es elektronisch erzeugen können. Hier gibt es rein synthetische Methoden oder auch die des „Samplers“, der gespeicherte Klänge aufruft und mischt.
Das „Wunder“ ist hier nicht die Elektronik oder die Schläue der Programmierer, sondern unser Ohr, das aus dem rein zeitlichen Signal einer Punktquelle einen kompletten Vielklang vermitteln und in Zusammenarbeit mit dem Gehirn und zwei Punktquellen (Lautsprecher z.B.) zu einem musikalischen Raum-Erlebnis zusammenbauen kann.
Diese „Struktur“ ist in uns drin, ohne dass wir etwas dafür können. Sie ist so ungeheuerlich effektiv, dass es schwerfällt, sie nachzubauen. Was ist daran Physiologie und was Psychologie? Wieso können wir unterschiedliche Instrumente erkennen, wenn sie den gleichen Ton spielen? Wieso mischt sich das nicht zu einer neuen Klangfarbe eines Hyper-Instruments? Addieren sich am Ende die Luftdruckwerte nicht (altes Superpositionsprinzip der Physik)? Doch, das tun sie ganz bestimmt, aber das Ohr im Zusammenspiel mit unserem Gehirn (und im Zusammenspiel mit unserer Psyche?) wertet offenbar komplexere Zusammenhänge aus, als nur einen einfachen Druck-Verlauf in der Zeit festzustellen.
Hierzu kann man einmal synthetische Klänge erzeugen und vergleichen. Oder zumindest erst einmal auf dem Papier Schwingungen überlagern und untersuchen, welche Hyper-STRUKTUREN dabei erkennbar werden. Das betrifft sowohl physikalische als auch „ästhetische“ Randbedingungen:
– Wer legt die Energie-Verteilung über die Obertöne fest? (Der Körper des Klangerzeugers über interne Rückwirkungen, das Übertragungsmedium durch frequenzabhängige Dämpfung, der Empfänger mit seinem Frequenzgang, …)
– Wer legt die Phasenlage der Obertöne fest?? (Ein Energie-Minimierungsprinzip, rückgekoppelt über die Gesamt-Elongation?)
– Gibt es Zeitkonstanten für solche Rückkopplungen? Wie lang muss ein Ton sein, damit sich seine Klangfarbe einstellt? Wie lang muss man ihn hören, um ihn einordnen zu können? Wie lang müsste das eine gute Technik „hören“? (Fourieranalyse erfordert mehrere Wellen, also Zeit…)
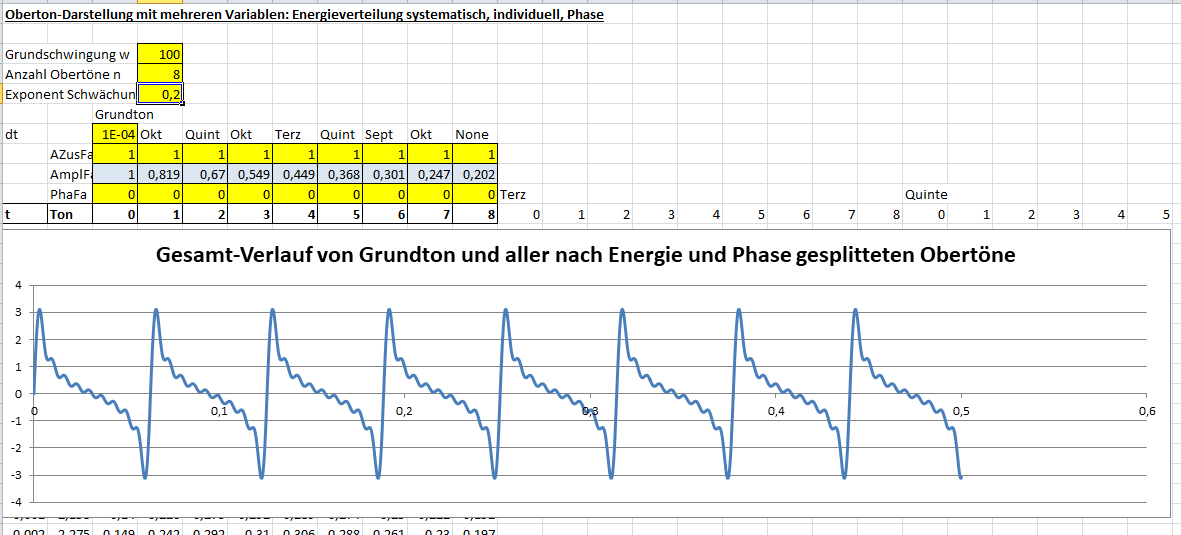
Hierzu noch einige Veranschaulichungen (Visualisierungen), nämlich eine grafische Synthese des Zeitablaufes einer Schwingung mit entsprechenden freien Parametern:

Acht systematisch und individuell veränderte Oberton-Energien samt individueller Phasenverschiebung (gleiche Frequenzen wie oben!)
Viel spannender als eine Visualisierung ist aber eine Modellierung, von der ich schon lange geträumt habe, weshalb ich sie jetzt (Weihnachten 2019) live umsetzen will.
Nimmt man zum Beispiel eine zweiseitig eingespannte homogene Saite (weitere schrittweise aufgebaute Beispiele: siehe die Schwingungs- und Wellen-Bahandlung im Physik-Part unter 2.4.1.1.2) und zupft sie an, kann man ja einmal untersuchen, wie sie sich im Zeitverlauf bewegt. Dabei kann man das Modell schrittweise der Realität anzupassen versuchen.
Schritt 1:
Wir gehen davon aus, dass wir die Saite nur leicht anzupfen und vernachlässigen deshalb eine Längsbewegung der Elemente der Saite, das heißt, dass nur die Kraftkomponenten senkrecht zur Einspannungs-Verbindungslinie beachtet werden. Die Startsituation ist ein flaches Dreieck, dessen Spitze (die Stelle, an der gezupft wird) variabel sein soll. Alle Elemente (z.B. aus Symmetriegründen eine ungerade Anzahl: 999 Stück Punktmassen) sind gleich schwer und sind äquidistant und durch identische Zugfedern (die Saite ist schließlich vorgespannt!) verbunden. Die Federn sollen hier keinerlei Biege-Steifigkeit haben! (Es werden also lediglich das Hookesche Gesetz der Porportionalität von Dehung und Spannung und das Newtonsche Gesetz der Proportionalität von Kraft und Beschleunigung genutzt und zweimal numerisch integriert.)
Dann gibt es (tatsächlich ein Zwischen-den Jahren-Programmier-Spaß 2019) ein überraschendes Bild, das bei näherer Betrachtung aber logisch ist:

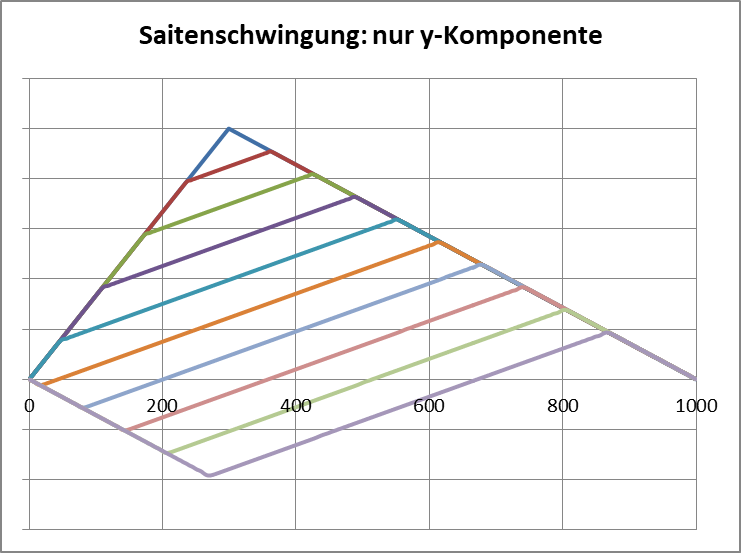
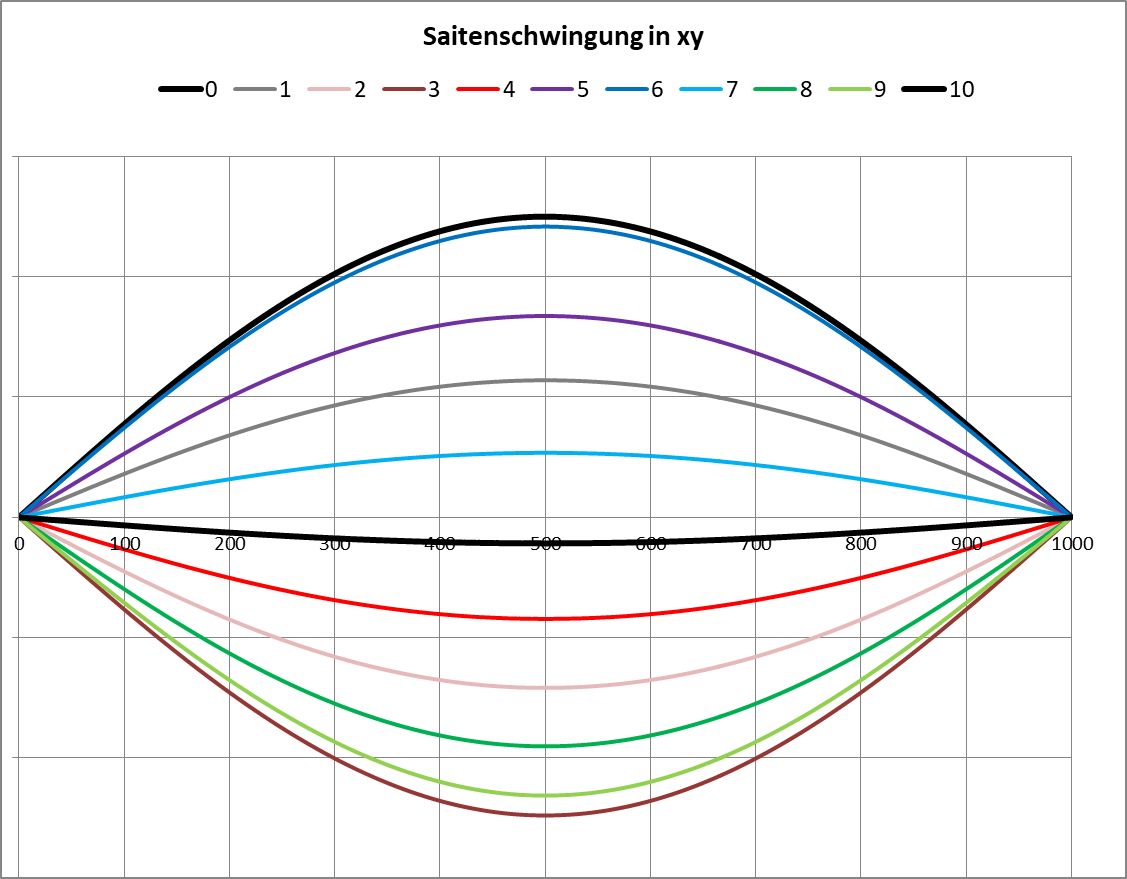
Knapp 10-fach überhöhte Momentaufnahmen der Saiten-Geometrie nach gleichen Zeitabschnitten (regelmäßige „Stroboskop“-Aufnahmen aus insgesamt 36.000 Schritten)
Man erkennt, dass das Dreieck immer wieder diagonal umklappt. (Hier und weiter unten sind die „Stroboskop“-Aufnahmen der Saite knapp 10-fach überhöht, damit man die Formen besser erkennen kann. In „Wahrheit“ wird das Saiten-Modell bei einer Länge von 1.000 Einheiten (1.000 linear elastische Federn mit Vorspannung mit je 1 Einheit Länge) nur 50 Einheiten weit angezupft! Für (beispielsweise) eine Cello-Saite von rund 69 cm freier Länge wären das dreieinhalb Zentimeter Auslenkung beim Zupfen, also ein ziemlich lauter und relativ unsauberer Pizzicato-Ton! (Die Grenzen der harmonischen Schwingung werden hier von mir absichtlich ausgelotet!) Das hier abgebildete „Geschlenker“ der Saite ist in der geometrischen Wirklichkeit also nur „halb so wild“ und wird wegen der hohen Geschwindigkeit auch vom Auge nicht so gut wahrgenommen. Mit einem schweren Gummiseil lässt es sich aber nachbilden!
Hier einmal die Eingabe-Felder meiner EXCEL-Tabelle für die Auswahl der Parameter:
Um die Zwischenschritte zu sehen, muss man den Numerik-Zeit-Takt verkürzen:
In Reinstform (also ohne Artefakte der Numerik) zieht sich die Biege-Steifheit-freie „Schnips-Gummi“-Saite einfach in geraden Linien straff. (Aus dem oben liegenden Dreieck des Starts wird also erst ein oben liegendes Viereck und dann ein sich selbst schneidendes Viereck und dann ein unten liegendes Viereck bis zum unten liegenden Dreieck als Wendepunkt. Die Geschwindigkeit nimmt nicht zu, aber die Länge des „bewegten Teils“, der „Abkürzung“. So scheint der Energiesatz (Pendeln zwischen elastischer potentieller und kinetischer Energie) erfüllt zu sein.
Natürlich kann man eine Dämpfung (geschwindigkeitsproportional zum Beispiel) einführen und erhält hier folgendes Bild:
Hier ist nun schon eine leichte Abrundung der Schwingung und der Geometrie zu erkennen. Aber das befriedigt natürlich noch lange nicht. Obwohl: Die erste Oberwelle der Schwingung wäre eine „ungerade“ Funktion, also z.B. eine komplette geometrische Sinuswelle, bei der der Saiten-Mittelpunkt ruht. Das kann man bei der Diagonal-Wanderung des Maximums durchaus erkennen. Und offenbar wird die Oberwelle stärker gedämpft als die „einbäuchige“ Grundwelle.
Schritt 2:
Wir führen eine „echte“ Zwei-Dimensionalität ein, indem bei einem unsymmetrischen (nicht gleichschenkligen) Start-Dreieck die Zugkräfte der Federn rechts und links vom Zupf-Punkt gleich gesetzt werden, wodurch der Zupf-Punkt zur Seite wandert. Dann machen wir nach echter 2-Komponenten-Kraft-Wirkung echte x-y-Plots der Feder-Situation und erleben tatsächlich eine Änderung, nachdem die Anfangs-Gerade jeweils an den Saitenenden und den eigenen „Eck-Formen“ der Saite schrittweise gekippt und geglättet wird. Jetzt sind auch höhere Oberwellen zu erkennen! (Man beachte aber auch hier, dass die laterale Wechselweikung in der Numerik nur 1 Element pro Takt beträgt, also schon 499 Takte erforderlich sind, um von der Mitte der 999-Elemente-Saite bis zum Rand zu gelangen. So erklären sich die am Ende über 100.000 Takte für etwa 1.000 Elemente, also 100.000.000 Kraft-, Beschleunigungs- und Orts-Berechnungen für jeden gewählten Parametersatz, die über 10 Minuten dauern.)
Die ungedämpfte Schwingung glättet sich, ohne dass der Anteil der Oberwellen zurückzugehen scheint. Das sieht schon wie ein „Einschwingen“ aus. Für eine erfolgreiche Fourier-Analyse braucht man noch ein paar mehr Schwingungen, hier sind es jetzt wenigstens 17 Stück (Neujahrstag). Interessant ist hier das Spiel mit dem Ort des Zupfens und dem daraus folgenden Oberwellen-„Spektrum“, was jeder Praktiker eines Saiten-Instruments kennt: Der Abstand zum Steg beim Zupfen oder Streichen beeinflusst die Klangfarbe stark.
Sogar bei der mittig gezupften Saite entwickeln sich Oberwellen bei der Reflexion an den Einspannstellen!
So. Nun ist der 01.01.2020, da kommt die Fourier-Transformation dran.
Zuerst wird die Schwingzeit und Phase der Grundwelle grafisch im Diagramm ermittelt und durch eine zusätzliche Funktion im Diagramm visuell geprüft.
Dann werden die Oberwellen als ganzzahlige Vielfache der Grundschwingung gesetzt und ihre Phase wieder im Intervall-Verfahren (hier noch per Hand) ermittelt. Dazu muss aber schon das Integral des Produkts von Original-Schwingung und Fourier-Komponente gebildet und maximiert werden. Die Maximal-Werte werden in ein Balkendiagramm eingetragen.
(Eine komplette Fourier-Transformation müsste programmiert werden, damit ein quasistetiger Durchlauf der Probe-Frequenz mit automatisierter Phasen-Prüfung zu einem „stetigen Spektrum“ führen könnte.)
Hier das Ergebnis, zuerst einmal für folgende Parameter ermittelt:
- Zupf-Punkt bei 25% der Saitenlänge
- Saitenspannung und Zupfweite so eingestellt, dass die Schwingung gerade noch stabil ist
- keinerlei Dämpfung, 108.000 Zeit-Takte
- Spektral-Daten z.B. für die Saitenmitte (50% der Saitenlänge)
Man erkennt zwei interessante „experimentelle“ Fakten:
a) Obwohl offenbar (auch ohne Biegesteifigkeit!!) durch eine laterale Mäglichkeit der Massenpunktverschiebung eine Glättung der Saitenkrümmung stattfindet, ist in der Saitenmitte der Anteil der antisymmetrischen Wellen verschwindend gering (Beachte die Zahlenwerte der Ordinate der blauen Balken im Vergleich mit den roten). Die Symmetrie der Anordnung bleibt somit gut erhalten.
b) Die Dreieck-Unsymmetrie des Starts führt zu geometrisch symmetrischen Oberwellen, die im Zeitablauf unsymmetrisch aussehen. Die ermittelten Intensitäten (zweite Zeile) und Phasenlagen (dritte Zeile) der Oberwellen sind für diesen Parametersatz wie folgt:
Die gute Übereinstimmung der punktierten schwarzen Kurve mit der glatten roten im dritten Diagramm der oberen Gruppe zeigt tatsächlich die Güte der Transformation.
Man sollte also den gleichen Aufwand für die beiden außermittigen Punkte bei 30% (oder 70%) der Saitenlänge treiben, um weitere Erkenntnisse zu gewinnen.
Zuerst ist es relativ einfach, einmal die experimentelle Schwingung beider Punkte in x-Richtung zu visualisieren und mit der Mitte zu vergleichen.
Aus Symmetriegründen (Lieblingssatz der Physiker!) darf man davon ausgehen, dass sich die Punkte bei 30% und 70% nicht unterscheiden, also:
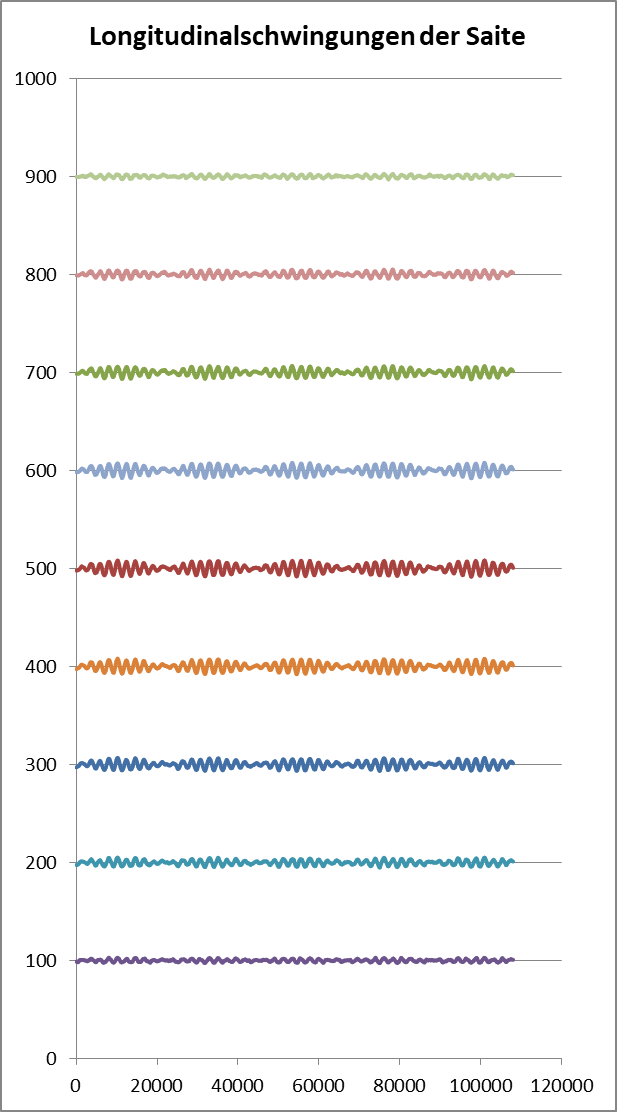
Interessant ist, dass auf die obigen etwa 17 Schwingungen senkrecht zur Saitenachse 5 Schwebungen längs zu ihr (Longitudinalwelle) auftreten (an den beiden hier gezeigten Punkten ähnlich!), die aus je etwa 10 Schwingungen bestehen. Auf etwa 50 Schwingungen in x (längs) kommen also etwa 17 in y (quer), also etwa 3:1, was nahelegt, dass die 2. Oberwelle (dreifache Frequenz), die wieder räumlich symmetrisch ist, wesentlich zur Längsbewegung beiträgt, was aber schwer verständlich ist. Erst recht ist die Schwebung, die als Überlagerung von nur 10% unterschiedlichen Frequenzen zu deuten ist, unverständlich. Das muss weiter untersucht werden, weil auch die Möglichkeit eines numerischen Artefaktes nicht auszuschließen ist: Wenn 1000 Elemente durchlaufen werden, ist nach 2000 Takten die Reflexion einer Singularität vollendet. Die beobachtete Schwebung ist nur unwesentlich länger. Zufall?
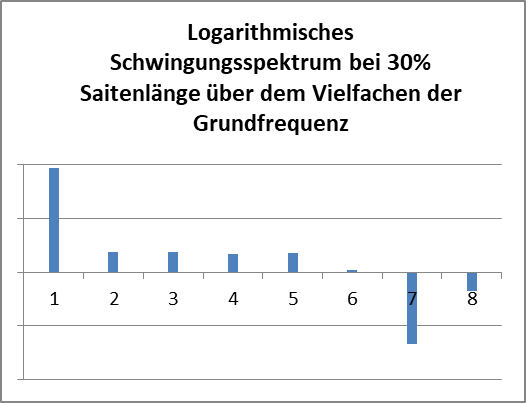
Und nun die Daten für den Saitenpunkt bei 30% der Saitenlänge:
Man erkennt sowohl im Zeitverklauf als auch im Spektrum die wesentlich größere Rolle der „antisymmetrischen“ Anteile, besonders den der ersten Oberschwingung, in deren Bauch-Nähe der Zupf-Vorgang erfolgte. Ebenfalls interessant ist, dass deren Einschwing-Vorgang offenbar länger dauert. Dabei wird offenbar die Schwingzeit der Saite etwas kürzer, was man im Vergleich der jeweilgen Spitzen mit der konstant frequenten FA-Kurve sieht. (Dazu unten mehr!)
Das „Wandern“ des Knickes der abfallenden Flanke sollte noch durchdacht werden: Offenbar haben auch die unsymmetrischen Oberwellen eine leicht andere Frequenzbasis als die Grundschwingung („Reflexion“ an den Saitenenden), was bei der Analyse nicht als Variable genutzt worden ist!
Die Längsschwingung des Punktes „30%“ ist schon oben abgebildet worden.
Zum Vergleich und weiteren Studium wird der Zupfpunkt von 25% auf 45% der Saitenlänge verschoben. Alle anderen Parameter bleiben gleich.
Man sieht an der Longitudinalschwingung zwei Unterschiede:
– sie ist schwächer (bei gleicher Schwebung)
– sie ist außerhalb der Mitte etwas „chaotisch“
Das Spektrum ist jetzt so aufgebaut:
Die Daten unterscheiden sich tatsächlich ein wenig, was der Erfahrung voll entspricht: Je weiter man die Saite „vom Steg weg“ anzupft, desto „weicher“ wird ihr Klang, desto weniger Energie steckt in den Oberwellen und desto ähnlicher sind sich die Phasenlagen. (Sogar eine minimale Anfangs-Frequenz-Änderung weist aus die Nichtlinearität des Dreieck-Starts hin: Schwingzeit von 6240 auf 6250 Einheiten verlängert. Das kennt auch der Bass-Zupfer: Bei übermäßig starkem Zupfen schleicht sich der Ton an den Endwert in etwa einer halben Sekunde an: Das sind etwa 50 Schwingungen, also dreimal mehr als hier überhaupt berechnet.)
(Ein Wort zu EXCEL-VBA: Wenn man Daten in Zellen schreiben lässt, die ihrerseits für Berechnungen innerhalb der Tabelle (Fourieranalyse zum Beispiel) benötigt werden, verlängert sich die Rechenzeit in VBA (25 Spalten mit 108.000 Zeilen mit Daten versorgen) enorm, weil die Prozedur offenbar für Tabellen-Kalkulation unterbrochen wird. 6 Prozesseoren sind dann nur zu 1% ausgelastet… Man sollte also besser alles im Hintergund mit Variablen belassen und nur solche Daten in die Tabelle bringen, die man direkt für Diagramme braucht – also filtern!)
Eine ganz andere Variation des „Versuchsaufbaus“ liegt beim „Zupf-Vorgang“ selbst: Wenn man nicht mit einem „echten“ gezupften Dreieck startet, sondern mit einer hypothetischen Sinuskurve, was passiert dann?
Hier der Sinus-Start als Strobo-Bild:
Wie man sieht: Wenn die Anfangsbedingungen der allgemeinen Lösung der Gleichung entsprechen, kann erwartungsgemäß nichts Unerwartetes passieren. (Das zeigt aber auch, dass die Numerik nichts verfälscht, also nicht ganz falsch sein kann!)
Die weitere Entwicklung bringt folgende Ergebnisse:
Man erkennt sehr schön, wie stabil die Saitenmitte ist. Obwohl beim Start KEINE longitudinale Anpassung über die Kurvenlänge (konstante Dehung aller Elemente!) erfolgt ist, stellt sich ein ausgewogener Zustand schnell ein, wie die Longitudinalschwingung bei 30% der Länge deutlich zeigt.
Die Frequenz ist übrigens etwas anders als beim echten Zupfen:
Noch einmal: Der Praktiker „Bassist“ weiß das: Wenn er sehr stark zupft, gleicht sich die Tonhöhe nach etwa einer halben Sekunde an (etwa 50 Schwingungen). Wir haben hier nur 17 Schwingungen analysiert und liegen deshalb mit einer Sinus-Schwingzeit von 6.230 Einheiten dann etwas unter der Zupf-Schwingzeit (also über der Frequenz) von 6.240 Einheiten des etwas tieferen Tones.
Schritt 3:
Berücksichtigung einer elastischen Biege-Steifigkeit. Hier könnte man mit einem Typ von Glättungs-Algorithmen arbeiten, wenn das energetisch passt, oder Drehmomente in jedem Punkt in benachbarte Kräfte umrechnen. Dazu sollte keine innere Schleife erforderlich sein. Um eine geometrische Wirkung des sequentiellen Abarbeitens zu vermeiden, muss wieder ein Zwischenzustand gespeichert werden, der dann am Ende des Zeittakts zurückübertragen wird.
Die erste Probe ist ernüchternd: Bezieht man nur die ersten Nachbarn rechts und links ein, gibt es entweder ein numerisches Aufschaukeln von Störungen (zuerst von den Saitenenden!) oder fast gar keinen Effekt außer geringfügig höheren Oberwellen, was den Erwartungen der „Glättung“ widerspricht und auf einen Zustand kurz vorm Aufschaukeln hinweist.
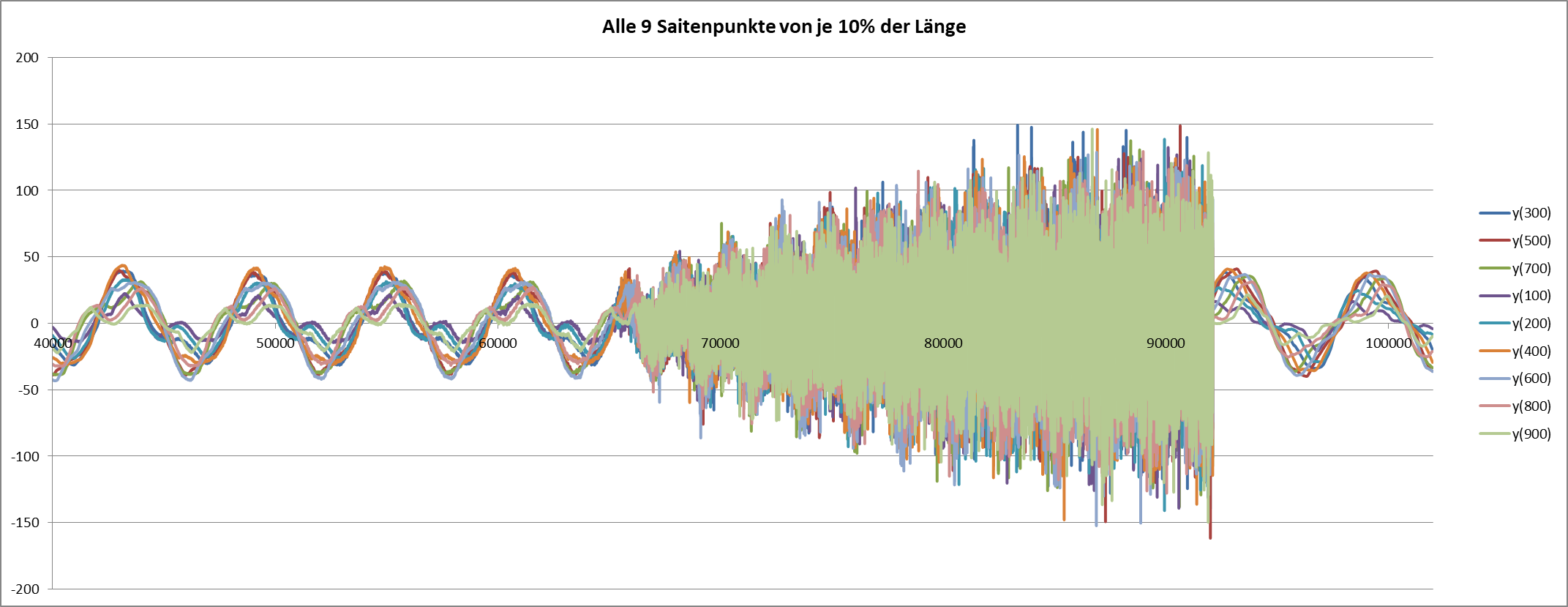
Man sieht hier den Schwingungsverlauf der 9 ausgewählten äquidistanten inneren Punkte bei einer kritischen Biegesteifigkeit. Die Rechnung wurde nach etwa 90 Prozent der Gesamt-Zeit abgebrochen. Dahinter sind noch die Werte der halben Steifigkeit zu erkennen, die sich weder vom Start mit der ganzen noch vom Gesamtverlauf der steifigkeitsfreien Werte wesentlich unterscheiden.
(Auf die Wiedergabe der weiteren Diagramme wird deshalb hier verzichtet, weil sie sich nicht unterscheiden!)
Physikalisches Fazit: Die zweidimensionale Behandlung der elastischen Längs-Feder-Wirkung reicht völlig aus, um den Vorgang zu beschreiben, weil auch sie allein schon zum Glätten einer nichtlinearen Struktur führt.
Die Frage nach der dritten Dimension wird hier nicht gestellt, weil die Anfangsbedingungen zweidimeniosnal waren. Natürlichb kann man eine Saite auch „dreidimensional“ anzupfen, indem man sie aus der Ruhelage zieht und senkrecht zur Zugrichtung „wegschubst“. Aus dem Superpositionsprinzip folgt, dass daraus für Auslenkungen, die klein gegen die Saitenlänge sind, keine neuen Grund-Frequenzen folgen. (Siehe x-y-Ellipse des z-Faden-Pendels.) Wie sich bei einer realen Dämpfung aber die Verhältnisse der Oberwellen verschieben, folgt daraus nicht. Das heißt, dass es nicht ausgeschlossen ist, dass auch hier eine zeitlich veränderliche Klangfarbe entstehen kann, so wie es bei Veränderung des zweidimensionalen Zupf-Ortes und der Zupf-Amplitude der Flle ist.
Das konstante Anstreichen einer Saite mit einem Bogen ist hier nicht modelliert worden.
Musik-praktisches Fazit:
Der Komponist spielt mit der Vielfalt der Klang-Farben, indem er die einzelnen Stimmen seines Werkes auf verschiedene Instrumente verteilt. Die Liebhaber von Opern und Sinfonien wissen das zu schätzen. Ohne das Wunder unserer Ohren und unseres Gehirns wäre das alles überflüssig, denn auf einem Einkanal-Oszillogramm wäre nur eine wüst geschlängelte Linie.
Eigenartigerweise überfordern Opern und Sinfonien häufig meinen ganz persönlichen Struktur-Fetischismus. Ein Konzert für Solo-Instrument und Orchester hingegen ist für mich immer ein Genuss. Da muss ich über meine Psyche (oder meinen beschränkten Struktur-Verstand?) offenbar noch einmal nachdenken…







































Kommentar abgeben