2.8.5 Trajektorien „ohne Rhythmus oder Struktur“: Interplanetare Reisen
Zur Erinnerung: Man hat einmal gelernt, dass die Bahnen um Himmelskörper (also: „Trajektorien im Schwerefeld“) in zwei Hauptgruppen unterteilt werden können:
– gebundene Bahnen (Ellipsen): Gesamtenergie aus potentieller und kinetischer ist kleiner als Null (Körper bleiben im Schwerefeld)
– ungebundene Bahnen (Hyperbeln): Gesamtenergie aus potentieller und kinetischer ist größe als Null (Körper kommen von außerhalb und verschwinden dorthin wieder)
Im Grenzfall Null ergibt sich als Bahn eine Parabel.
(Das sind natürlich auf genügend hoch abstrahierter Betrachtungsebene ebenfalls „Strukturen“, auch wenn ihnen kein „Rhythmus“ im Sinne einer Wiederholung innewohnt!)
Man liest in der Zeitung bei Weltraum-Missionen zu anderen Planeten und ihren Monden oder zu den Asterioden oder Kometen immer wieder vom „Schwung-Holen“ zwecks Energie-Einsparung (Kraftstoff-Reduzierung und also Startmasse-Reduzierung der Trägerrakete). Das klingt auf den ersten Blick wie ein Verstoß gegen den Energiesatz. Wie muss man sich das vorstellen und wie kann man das mit unseren bisherigen Erfahrungen mathematisch bewältigen?
Die Transfer-Bahn zum Untersuchungsobjekt wird durch Himmelskörper beeinflusst, gegen welche die Sondenmasse vernachlässigbar ist (ein „gemenisamer Schwerpunkt“ spielt also keine Rolle).
Vorüberkegung 1: Transferbahn zum Nachbarn
Das am stärksten vereinfachte Bild einer Bahn von der Erde zum Mars ist also eine Ellipse um die Sonne, die beide Bahnen (hier zwei konzentrische Kreise in der gleichen Ebene) tangiert:
Rechts startet die grüne Raumschiff-Bahn nach der ersten Beschleunigung als Tangente an die blaue Erdbahn. Das Raumschiff muss mindestens die zweite kosmische Geschwindigkeit (bezogen auf die Erde) haben, genauer: eine solche, die (bezogen auf die Sonne) bis zur roten Mars-Bahn reicht.
An der roten Bahn angekommen, muss wieder beschleunigt werden (!!), um auf der roten bleiben zu können.
Dann ist (vorausgesetzt, man ist tatsächlich in der Nähe des Roten und nicht „nur“ auf seiner Bahn) ein günstiger Landemodus (unter Berücksichtigung der Eigenrotation des Roten) zu finden.
Die Wirklichkeit ist wegen der Kraftfelder beider Planeten und der Ellipsenform ihrer Bahnen (incl. ihrer Neigungen etc.!) viel komplizierter.
Gehen wir nun zum eigentlichen Problem dieses Abschnitts, nämlich dem „Schwungholen“, über, so müssen wir schon hier feststellen, dass wir ständig das Bezugssystem gewechselt haben (müssen): Zuerst findet der Start im Bezugssystem der Erde statt, dann erfolgt der Transfer im Sonnensystem zum Mars, und dann landen wir im Mars-System.
Nutzen wir nun den Mars zum Schwungholen auf dem Weg zum Jupiter, gibt es weitere System-Wechsel.
Bei jedem Wechsel gibt es eine kleine Schwierigkeit: Die kinetische Energie ist als geschwindigkeitsabhängige Größe natürlich nicht einmal invariant bei einer einfachen Galilei-Trafo (gleichförmig gegeneinander bewegte Bezugssysteme), Längen, Zeiten und Beschleunigungen dagegen aber schon.
Es gibt natürlich immer die Lösung, alles in ein einziges Bezugssystem zu packen, wozu sich hier die Sonne anbietet. Die vorher (2.8.4.) angestellten Übungen zur gegenseitigen Schwerkraft-Beeinflussung bewegter Körper waren also sehr sinnvoll!
Vorüberlegung 2: Schwungholen im geozentrischen System am Mond
Der Start erfolgt von der Erde unter Ausnutzung der Eigenrotation. Es folgen jetzt mehrere Bahnbilder, bei denen lediglich die relative Position des Mondes auf seiner Bahn zum Raketenstart verändert worden ist (also andere Startort-Uhrzeit). Alle anderen Parameter sind gleich geblieben. Es zeigt sich, dass für die „Schwung“-Nutzung des Mondes ein sehr schmales Fenster zur Verfügung steht. Diese Startposition des Mondes ist durch den hellgrauen Kreis gekennzeichnet. Zehn Takte der Gesamtzeit sind durch Verbindungslinien hervorgehoben worden.
Hier zwei für unsere Zwecke noch ziemlich unglückliche Parametersätze.
Der Bahnstand des Mondes unterscheidet sich hier nur um 1°, und doch sieht man das Umkippen der Trajektorie vom starken „Zurückweisen“ zum scharfen „Wegschleudern“. Man muss allerdings beachten, dass hier Numerik-Artefakte vorliegen können, wenn die Masse-Abstände zu gering werden, weil der Zeittakt der Geschwindigkeit nicht angepasst wird. Intelligenter (und aufwändiger) sind dagegen Ort-Takte. Deshalb jetzt eine besser geglättete Gegenüberstellung 3° später (sieht man im Diagramm, wenn man genau hinguckt!):
Der Bahnstand des Mondes unterscheidet sich hier um 4°, was eine elegantere Bahn ergibt. Rechts noch ein anderer Vergleich, wenn man die Mondmasse verschwindend gering macht. Es bleibt die „mondlose“ Ellipse um die Erde stehen.
(Für die Insassen eines Raumschiffes ist das übrigens völlig ohne Belang, wie stark die augenblicklich wirkende Schwerkraft ist, bezüglich ihres Raumschiffes sind und bleiben sie „schwerelos“.)
Die Vielfalt der zu beachtenden Parameter ist schon hier nicht unerheblich. ABER: In der Wirklichkeit kommen noch die Berücksichtigung der Neigung der Erdachse und der Mondbahn hinzu und auch die „Geoid-Wirkung“ (da war doch was…) der Form der Erde sowie die Bahnebene des späteren Ziel-Planeten. (Fehlerrechnung wird hochinteressant, passt aber nicht hierher!!!)
Modell mit drei Planeten
Wenn man mit diesen Kenntnissen nun ein Modell aus drei Planeten baut, wobei man vom inneren startet, vom mittleren Schwung mitnimmt, um dann zum äußeren gelangen zu können, sieht das so aus (10.000 Integrationsschritte):
Bei diesen beiden Datensätzen des Modells wurde einzig und allein die Ausgangsposition des mittleren Plaenten verändert. Die Empfindlichkeit des Systems gegen Änderung dieser Größe ist naturgemäß um so größer, je näher die Sonde dem mittleren Planeten (nicht seiner Bahn als solcher!) kommt. Man erkennt, dass man in Wirklichkeit die Planetenkonstellation nicht ändern, sondern nur nutzen kann. Ändern kann man nur den Startzeitpunkt der Sonde und ihre Anfangsbahnwerte und unterwegs relativ wenig mit Bahnkorrekturen, solange der Treibstoff reicht.
Noch ein Spiel mit den Parametern und eine Zusatz-Darstelllungs-Form seien hier erlaubt:
Links sind Zeittakte hervorgehoben (Mars und Sonde synchronisiert), rechts sind Erde und Sonde auf das Marssystem transformiert worden. Die Überholvorgänge der Erde bilden in der x-y-Ebene Schleifen. Der Jupitereinfluss knickt die Sonden-Bahn ein zweites Mal, und zwar stärker als der Mars.
Übrigens: Die echten Sonden zu den Asteroiden und Kometen der letzten Jahre haben gleich mehrere Transits von Planeten und Kometen zur Bahnkorrektur genutzt, was eine mathematische und steuertechnische Meisterleistung erster Güte darstellt!
Nachbetrachtung:
Was ist eigentlich mit dem Energie-Satz angestellt worden, dass er das Schwungholen erlaubt?
Dazu noch einige Überlegungen:
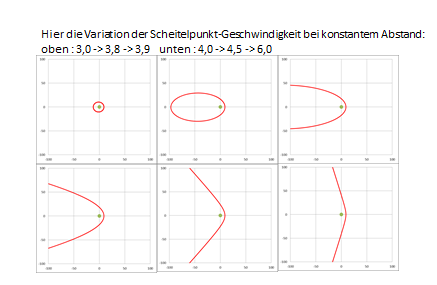
Bezüglich des Schwung-Gebers gibt es einen ungebundenen Zustand, also eine Hyperbel-Bahn folgender Art, je nach Energie (Geschwindigkeit) oder Abstand:
Bei diesen Hyperbel-Bahnen kann man also von einer Art sanfter Reflexion sprechen, wobei offenbar ein Impuls-Austausch stattfindet. Legt man den Ursprung in die Zentralmasse, hat man diese sozusagen unendlich schwer gemacht und braucht ihren Impuls nicht zu berücksichtigen. „In Wirklichkeit“ aber ist sie nicht unendlich schwer und nimmt den Gegenimpuls, der den Richtungswechsel der Sonde ausgleichen muss, auf. Der gemeinsame Schwerpunkt dagegen bleibt in Ruhe.
Befindet sich diese Zentralmasse aber selber in einem Umlauf um ein noch größeres Zentralgestirn, so ändern sich durch ihren Zusatzimpuls ihre Bahnparameter.
Man erkennt auch hier ohne weitere Rechnung, dass es für Energie-betrachtungen schwierig ist, zwischen verschiedenen Bezugssystemen zu wechseln.
Beim obigen Spiel von Erde-Mars-Jupietr-Raumschiff verhalten sich die Geschwindigkeiten wie folgt:
Das Raumschiff (vr) verlangsamt sich anfangs beim Aufsteigen zum Mars, dann wird es schneller und verlangsamt sich wieder zum Jupiter hin, aber auf einem höheren Niveau, als es ohne Mars geschehen wäre, und wird dann vom Jupiter regelrecht „geschleudert“, bevor es sich wieder weiter nach außen verlangsamt (falls sie nicht für die Landung abgebremst worden ist).
Eigentlich hätte das Raumschiff schon beim Kreuzen der Marsbahn eine geringere Geschwindigkeit als dieser haben müssen, wie hier für den doppelt langen Zeittakt und ohne „Schwungholen“ dargestellt:
Zum Abschluss noch ein Parameter-Beispiel für zwei etwa gleich-große Schwung-Geschwindigkeiten (wieder einfacher Zeittakt):
(Die hohe Anfangsgeschwindigkeit („zweite kosmische“) des Raumschiffs war zum Verlassen der Erde erfoderlich.)
Hier die Schwung-Hol-Situation qualitativ gezeichnet:
Skizze für die beiden sich gegenseitig aufhebenden Austausch-Impulse von Raumschiff (4 Antennen) und Planet, beide auf Bahnen um die Sonne. Der den Planeten betreffende Gegenimpuls ist bezüglich seiner Bahn nach hinten außen gerichtet, verlangsamt ihn also einerseits und ändert andererseits zusätzlich seine Bahn-Exzentrizität.
Bei einem kleinen Raumschiff ist das unwesentlich, ein größerer Komet oder Asteroid aber würde „Schaden“ anrichten können.
Geht man von den bisher verwendeten Spiel-Daten für die halbquantitative Erkenntnisgewinnung zu einigen „echten“ Daten unseres Sonnensystems über, so ergeben sich folgende interessante Erkenntnisse für einen Flug zum Jupiter über den Mars:
- Die Empfindlichkeit des Systems gegen kleinste Parameter-Änderungen ist sehr groß:
Die Marsposition wurde also nur um 0,0001° seiner Bahn gedreht, und schon sieht der Schwung ganz anders aus. Das erhellt sofort, wenn man in den Himmel schaut und den Mars-Öffnungswinkel abzuschätzen versucht…
Wenn nun noch der Einfluss des Jupiters berücksichtigt werden soll, wird es noch verrückter:
Hieraus erhellt auch, dass man unterwegs Bahnkorrekturen vornehmen können sollte, also nicht ausschließlich für die Landung Treibstoff benötigt. Aber wer will schon auf dem Jupiter selbst landen? Seine Monde sind da interessanter. Aber hier endet nun meine Modellier-Lust, denn verstanden hat man genug: Es ist ein Riesen-Aufwand, alle Parameter unter einen Hut zu bringen, und das in „Wirklichkeit“ in 3 Dimensionen!!!
Aber beim Spielen mit den Parametern entdeckt man trotzdem interessante Details, die einem an sich klar sein sollten, aber dann doch frappierend sind. Ich wollte den Jupiter mal weit wegen haben, damit er nicht stört, und auf einmal sauste die Sonde vom Mars aus weit davon. Wieso denn das?
Der „gegenüber “ liegende Jupiter hat immerhin noch so viel Anziehungskraft, dass er die Sonde ein winziges bisschen näher an den Mars gezogen hat, do dass dieser einen viel größeren „Schwung“ vermitteln konnte. Da ich mir auch den Zentralabstand ausgeben lasse, musste ich allerdings feststellen, dass die Sonde den Mars gar nicht passieren konnte, weil sie aufgeschlagen wäre, hätte ich diesen mit seinem echten Radius (und nicht als Punktmasse) eingegeben. Man sieht also, was man bei einer „echten“ Weltraum-Mission so alles beachten muss…
Kurze Nachbemerkung zum Typ des Kraftfeldes:
Ändert man den Exponenten des Kraftfeldes in Schritten von o,5, so erhält man folgende vergleichende Übersicht für identische Startsituationen (Ort und Geschwindigkeit):
Um die dazugehörigen Potentiale (alle rotationssymmetrisch, weswegen es IMMER den (meist labilen) Sonderfall Kreis-Trajektorie gibt) darzustellen, werden drei typische ausgewählt:
Kugel (p1)- und Zylinder (p3)-Potential des Schwere-Typs, elastisches (p2)
Nur in zwei Fällen dreht sich die elliptische (präzedierende) Rosetten-Trajektorie zur stationären Ellipse ein: Kugel (rot) und Elastik (blau). (Im elastischen Potential ist ein Nulldurchgang physikalisch möglich, im gravitativen nicht.)
Es gibt auch andere stationäre Zustände, die dann sogar an „Elektronen-Orbitale“ erinnern:
Hier ist die grüne Trajektorie vom Kraftgesetz-Exponenten -2,495 bestimmt. (100.000 numerische Zeittakte für 2 Umläufe)
Hier ist die grüne Trajektorie vom Kraftgesetz-Exponenten -2,72 bestimmt. (100.000 numerische Zeittakte für 2 Umläufe)
Der grundsätzliche „Nachteil“ dieser letzten beiden grünen „Orbitale“ ist aber, dass sie nicht generell Formtyp-stabil sind, sondern eine Schwebung darstellen, die vom Wertepaar Kraftfeld-Exponent und Energie abhängt, dass sie sozusagen „Eigenwerte“ des Kraftfelds darstellen (also so etwas wie „gequantelt“ sind). Dasw zeigt eine leichte Änderung der Parameter sehr deutlich:
Hier ist zum vorherigen Wertepaar lediglich die Startgeschwindigkeit um etwa 5% von 0,61 auf 0,64 und 0,58 geändert worden, und sofort ist wieder die Präzession da.
Hier ist dafür der Exponent des Kraftgesetzes um etwa 0,5% von -2,72 auf -2,733 und -2,707 geändert worden.
(Die Vergleichsbahnen – rot und blau – zeigen übrigens gut, welcher Parameter geändert worden ist: Geschwindigkeit für alle drei, Exponent nur für die grüne.)
Daraus folgt im Umkehrschluss, dass man für vorgegebene Energien passende Exponenten oder für vorgegeben Exponenten passende Energien „finden“ kann, für die „stabile“ (d.h. stationäre labile) Zustände herrschen. Beispiel: Je zwei Wertepaare für zweimal gleiches „Orbital-Outfit“ unterschiedlicher Exzentrizität (Energie): Höhere Energie bei gleichem Startpunkt im rechten Scheitel (linke Bilder, alle drei Bahnen) ergeben hier geringere Exzentrizität (Veränderung in Richtung Kreis), größerer Exponent des Kraftfeldes (nur der grünen Bahn, obere Bilder) ergibt den stärker „eingedrehten“ Typ der stationären Trajektorie („2D-Orbital“ im 3D-Feld):
Das FAZIT aller bisherigen Variationen der Parameter ist, dass die berühmte und bekannte Kepler-Ellipse zwei Voraussetzungen erfordert:
- 3D-Gravitationsgesetz mit exaktem Exponenten (naturgegeben)
- Kugel-Symmetrie der Zentralmasse (sehr selten zufällig gegeben)
Dagegen ist es NICHT erforderlich, dass die Probemasse vernachlässigbar klein ist, wenn man die entstehenden synchronisierten Ellipsen (siehe in 2.8.4 das extreme Beispiel Doppelstern) um den gemeinsamen Schwerpunkt im 2-Körper-System als „Kepler-Ellipsen“ akzeptiert.
Ist KEINE Kugelsymmetrie der Zentralmasse vorhanden, entsteht eine Präzession, die eine Folge vom Auseinanderfallen von Masse-Schwerpunkt und virtuell mitwanderndem Gravitations-Zentrum ist (siehe 2.8.3). Auch eine virtuelle Änderung des Exponenten des Kraftgesetzes (s.o.) führt bei Bezug auf eine Punktmasse zu einer gleich gearteten Präzession. Kreisbahnen oder Ellipsen-Schwebungen sind dann als zufällige und labile geometrisch-energetische Zustände anzusehen.
Das beste und anschaulichste praktische Beispiel für die Präzession einer Bahn um eine von der Kugel abweichende Zentralmasse ist das zeitliche Verhalten der in der Dämmerung auftauchenden Internationalen Raumstation ISS (siehe numerische Integration, Beispiel 4).
(Sie war sozusagen der Ausgangspunkt für die Erstellung des Abschnitts 2.8.!)