2.10.2 Stationäre Zustände in „diskreten“ Systemen
Worin bestünde ein „stationärer Zustand“, wenn ein System „diskret“ ist? Wir fordern einfach, dass sich dieser Zustand (wie auch im stetigen System) als stabiles Gleichgewicht gegensätzlicher Prozesse einstellt. Gäbe es dafür ein anschauliches UND einfaches Beispiel?
Folgendes Experiment:
Wir lassen einen Ball schräg auf das obere Ende einer Treppe aus gleichen Stufen fallen. Der Ball kann die Treppe herunterspringen, im Idealfall Stufe für Stufe.
Frage: Stellt sich eine konstante Sprunghöhe (relativ zur jeweilgen Stufe) von allein ein?
Überlegung: Wenn es einen Energieverlust pro Reflexion auf der Stufe gibt (leicht unelastischer Stoß), der dem Energiegewinn durch Annäherung an das Schwerezentrum (potentielle Energie des Erd-Schwere-Feldes) gleich ist, dann sollte die Sprunghöhe über jeder Stufe gleich sein können.
Das leuchtet ein. Aber die Frage lautet ja, ob sich das von allein als echtes Gleichgewicht einstellen würde, dass also jede Abweichung von ihm zu einer „rücktreibenden Kraft“ zum Gleichgewicht hin führen würde?
Die Antwort ist leicht, wenn man die beteilgten Größen genauer unter die luoe nimmt:
Der Energiegewinn pro Stufensprung ist konstant, wenn die Stufenhöhe der Treppe konstant ist.
Der Energieverlust ist bei gegebenem (und konstantem, also von der Sprunghöhe unabhängigen!) Elastizitätsgrad eine relative Größe, die entweder auf die kinetische Energie selbst oder auf die Geschwindigkeit bezogen werden könnte. Bei genauem Nachdenken erkennt man, dass die Rückkopplung in jedem Fall negativ ist: Je höher der Ball springt, desto höher ist sein absoluter Energieverlust, wenn der relative Verlust (laut Aufgabenstellung konstant) ist. Deshalb sollte ein Ausgleichsprozess stattfinden, dessen Ergebnis genau di Sprunghöhe ist, bei der sich energetische Gewinn und Verlust ausgleichen.
Modelliert man das in VBA und stellt es in einem EXCEL-Diagramm dar, sieht das Ergebnis für die Fälle „zu kleiner“, „mittlerer“ und „zu großer“ Anfangs-Sprunghöhe so aus:
Erkenntnis:
Allein das Gegenspiel konstanter und relativer Größen kann schon zu einem „stabilen“ Prozess-Zustand führen, sogar in „diskreten“ Systemen.
Aufgabe für den Leser: Weitere Beispiele finden und modellieren und prüfen, ob diese allgemeine Behauptung widerlegt werden kann.
(In meinem Beispiel wurde übrigens vorausgesetzt, dass der Ball weder horizontale Geschindigkeit verliert noch anders als genau ein einziges Mal pro Stufe aufspringt. Das erfordert Übung im Experiment!)
Der Rechenkern ist wieder einfach:
(Der Elastizitätsgrad des Balls wurde energiebezogen in % eingegeben, deshalb die Wurzel und die Division durch 100. Das n ist die Nummer der erreichten Stufe mit der konstanten Stufenhöhe sth. Um eine zufällige Oszillation im Zeitintervall dt um die Stufe selbst zu verhindern, ist eine y-Korrektur in der if-Verzweigung enthalten, die bei kleinem dt nur wenig ins Gewicht fällt.)
Nachbemerkung:
Ein stationärer Zustand stellt sich auch dann ein, wenn man die Potenz des relativen Gegenwerts ändert (solange es eine monotone Funktion bleibt). Deshalb verändert sich nur der stabile Zahlenwert, wenn man die Gegengröße aus der Elastizität selbst statt aus ihrer Wurzel berechnet.
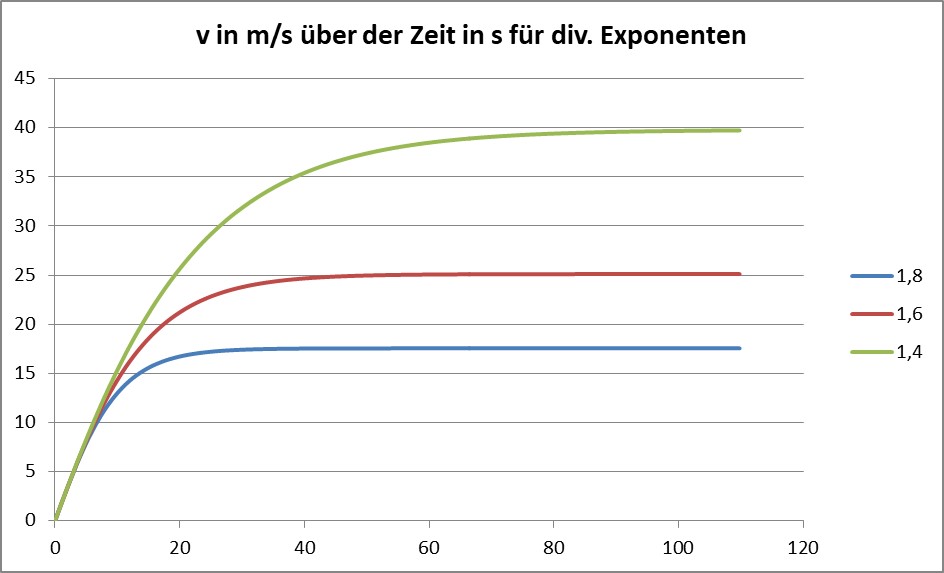
Das gleiche gilt zum Beispiel (hier mal eines selber gerechnet, natürlich numerisch, also irgendwie auch „diskret“, wie es in der Überschrift heißt) für die Abfahrtsgeschwindigkeit bei konstanter Neigung (einer Straße beim Radfahren oder eines Hangs beim Skifahren), wo der konstanten Hangabtriebskraft eine variable Luftwiderstandskraft gegenübersteht, deren Abhängigkeit von der Geschwindigkeit man normalerweise mit einer Potenz zwischen 1 und 2 ansetzen kann:
Je stärker die Abhängigkeit der Bremskraft von der Geschwindigkeit ist, desto eher stellt sich der Endwert ein und desto niedriger ist er.
(Hangneigung, Widerstandsbeiwert, Fläche quer zur Fahrtrichtung und Masse sowie Erdbeschleunigung jeweils gleich angesetzt.)
Das hier angeführte Beispiel ist auch aus wissenschaftshistorischer (und damit philosophischer) Sicht interessant, denn es schafft einen guten Kompromiss zwischen der peripatetischen Dynamik seit Aristoteles („je größer die Kraft, desto höher die Geschwindigkeit“, was eine Alltagserfahrung aus der Zeit der Zugpferde ist!) und der Newtonschen Dynamik („je größer die Kraft, desto höher die Beschleunigung“, was nur reibungsfrei gilt, zum Beispiel im Kosmos!): Beim Start steigt die Geschwindigkeit bei konstanter Kraft linear (Newton), dann pegelt sich ein konstanter Wert der Geschwindigkeit ein (gestiegene Reibungskraft gleich konstanter Antriebskraft, also Aristoteles!).




Kommentar abgeben