4.3.1.5 Musik und Mathematik sowie Physik: Wohltemperierte Stimmung
Woran merkt man, ob die Stimmung eines Instrumentes „wohltemperiert“ ist?
Was ist das überhaupt, ein „wohltemperiertes Klavier“, wie es bei Bachs Sammlung von Präludien und Fugen heißt, und kann man das hören?
(Zumindest kann man das erleben, wenn man das erste Mal ein Klavier zu stimmenr versucht und kurz vorm Verzweifeln darüber ist, dass dieguten Erfahrungen vom Stimmen einer Gitarre oder Violine nicht hinreichend sind! Heute gibt es dafür elektronische Hilfsmittel, die jedermann billig nutzen kann und somit nicht mehr gewzungen ist, sich harmonische Grundfertigkeiten des Hörens anzueignen…)
Das Problem ist auch in den Abschnitten 4.2.2 und 4.3.1.2 schon erwähnt und erklärt worden. Hier wollen wir es uns aber genauer ansehen, und zwar im Schwingungsbild und im Spektrum.
Ganz „einfach gefühlt“ ist es so, dass eine „reine Quinte“ so etwa wie „hohl“ klingt, eine wohltemperierte aber etwas „wärmer“ oder „voller“. Fachleute wie Orgelbauer oder Klavierstimmer erkennen die wohltemperierte Quinte an einer bestimmten Schwebung der Obertöne. Das schaffen wir Laien nie! Die Unterschiede bei den Intervallen sind nur schwierig aufzuführen, da es viele Konventionen gibt, wie man die nicht-trivialen Intervalle durch Stapelung aus den trivialen erzeugt. Die Fachleute nennen dann den (logarithmischen, also stapelbaren) Hundertstel-Teil eines wohltemperierten Halbtones „Cent“ (12 Halbtöne sind eine Oktave und also 1200 Cent):
| Intervall | einf.rational | Cent rein | Cent wt. | Abw. |
| Halbton | 105 | 100 | -5 | |
| Ganzton | 9:8 | 204 | 200 | -4 |
| kl.Terz | 6:5 | 316 | 300 | -16 |
| gr. Terz | 5:4 | 386 | 400 | 14 |
| Quarte | 4:3 | 498 | 500 | 2 |
| Tritonus | 603 | 600 | -3 | |
| Quinte | 3:2 | 702 | 700 | -2 |
| kl. Sexte | 814 | 800 | -14 | |
| gr. Sexte | 884 | 900 | 16 | |
| kl. Septime | 996 | 1000 | 4 | |
| gr.Septime | 1095 | 1100 | 5 | |
| Oktave | 2:1 | 1200 | 1200 | 0 |
Die Tabelle zeigt die Unterschiede gut. (Die leeren Felder können unterschiedlich gefüllt werden, das interessiert hier aber nicht.)
Wie sieht es grafisch aus? Dazu habe ich mir in EXCEL eine Überlagerung der einzelnen Schwingungen gebaut, für die ich die Parameter Frequenz, Phase und Amplitude eingeben kann, um sie in der Zeit einzeln darzustellen oder zu überlagern. Eine Fourier-Analyse des fertigen Schwingungsmusters soll zeigen, ob erstens alles gut angekommen ist und zweitens die Fourier-Analyse (das ist die Analyse, welche Frequenzen mit welcher Intensität im Gesamtmuster enthalten sind, wobei sich die Phase nur in der Verteilung des Peaks ober- und unterhalb der Nullinie äußert und in Bezug auf die Phase der Analysefrequenz gilt – schwierig klingt das, aber einfacher geht’s nicht) fein genug angelegt ist, auch andere Bewertungen zu erledigen.
Hier folgen jetzt ein paar Beispiele mit wachsender Konplexität.
Wir fangen trivial an, mit der Oktave, denn die ist immer und überall unbestritten die doppelte Frequenz. Wir können an diesem einfachen Beispiel das Lesen der Diagramme einüben.
1. Oktave c‘-c“ (das ist die normale Singstimmenlage für Frauen und Kinder, wie sie auch auf der C-Blockflöte in der unteren Oktave vorkommt: c‘ mit 264 Hz und c“ mit 528 Hz)
Wenn wir keine Phasenverschiebung nehmen und beide Töne als Schwingungen mit dem „positiven“ Maximalausschlag (bei einer Gitarren-Saite also zur gleichen Seite gezupft) beginnen lassen, sieht das so aus:
Zuerst wird jetzt immer ein kurzer Ausschnitt aus den Einzelschwingungen gezeigt (Amplituden und Phasen – ganz links beim Start! – und auch die Schwingzeiten – reziproke Frequenz – sind dort gut zu erkennen), dann die zusammengestzte Schwingung, die den Schalldruck erzeugt, dann ein Gesamtbild der Schwingung über eine ganze Sekunde und zum Schluss schließlich das Spektrum, dass rückwärts wieder aus dem Sekundenbild rechnerisch durch Fourier-Analyse (siehe dort) gemessen wird.
Man fragt sich sofort, warum das Gesamt-Sekunden-Bild so unsymmetrisch ist. Man erkennt es schon im zweiten Bild, dass das offenbar an der Phase liegt. Startet man die Oktave anders als den Grundton, kann man das ändern:
Unser Ohr macht keinen Unterschied aus der Seite, nach welcher die Saite angezupft wird. Unser Ohr macht eine Fourier-Analyse und mit dem Kopf eine Zuordnung über die Klangfarbe zu einem Instrument, und doch wollen wir genau deshalb, um unser Ohr noch mehr lieben zu lernen, hier alle Unterschiede herausarbeiten.
2. Dazu beginnen wir mit der Quinte (hier: c‘-g‘), die als Symbol für die Systematik der Harmonielehre gilt (siehe Quintenzirkel), und bei der schon alle Probleme auf einmal auftreten.
Zuerst also die reine Quinte, wie sie als natürlicher 2. Oberton auftritt, nämlich als dreifache Frequenz des Grundtons eine Quinte über der Oktave, die selber als 1. Oberton eine Oktave über dem Grundton liegt. Um es übersichtlicher zu machen, spielen wir den 1. Oberton mit dem 2. Oberton als zwei verschiedene neue Grundtöne, auf denen wir später wieder Obertöne aufbauen können.
Wir haben wieder ohne Phasenverschiebung gearbeitet und erhalten ein unsymmetrisches Bild. Das stört uns nun aber nicht mehr. Deshalb können wir gleich zur „wohltemperierten“ Quinte übergehen, die nicht mehr im reinen Oberton-Verhältnis zum Grundton steht, dafür aber beliebig stapelbar im Sinne der Gleichberechtigung aller Tonarten geworden ist, wie es spätestens seit Bach gang und gäbe ist. Und es ist wirklich zu sehen, dass da etwas „passiert“ ist:
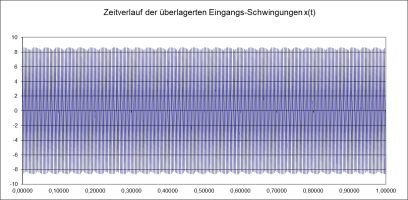
In den ersten beiden Bildern ist zu wenig Zeit vergangen, als dass wir die geringen Frequenzunterschiede schon sehen könnten. Aber im 2-Sekunden-Bild der Gesamtschwingung erkennen wir eine „Schwebung“ der überlagerten Schwingungen, die sich als rhythmische Lautstärke-Änderung bemerkbar macht. Am lautesten ist es immer bei der größten Gesamt-Amplitude, also zwischen den Abszisenwerten der „Kerben“: 4 mal in 2 s, also etwa mit 2 Hz. (Diese dient also den Fachleuten zum Erreichen der „wohltemperierten“ Stimmung beim Arbeiten an den Spannungen der Klaviersaiten oder den schwingenden Längen der Orgelpfeifen! Beim Kammerton a‘ sind das dann also knapp 4 Hz nach unseren ermittlungen hier…) Im Spektrum ist ebenfalls eine kleine Änderung zu sehen, nicht in der Lage der Peaks, wohl aber in ihrer Ausbildung: Da das Abtasten bei bestimmten und endlich vielen Frequenzwerten geschieht, ergibt sich zufällig der beginn eines „Doppel-Peaks“, der auch etwas nach unten ausschlägt. Das haben wir schon oben bei der Oktave in Reinstform gesehen!
Zur weiteren Übung nehmen wir nun noch für beide Töne der Quinte die jeweils ersten beiden Obertöne hinzu und basteln dann an den Phasen, bis das Schwingungsbild „schön“ symmetrisch wird (wie das Schlackern einer Saite zu Phasenänderungen führt, können wir uns überlegen: Knoten an den Saitenenden bleiben auf alle Fälle dort, aber eine reine „Gegenschwingung“ sollte schon wahrscheinlich sein, wobei gerad- und ungeradzahlige Oberschwingungen sicherlich unterscheidbar sein sollten…)
Wir beginnnen wieder mit der reinen Quinte:
Hier erleben wir zum ersten Mal, was „natürliche“ Intervalle sind: Der 2. Oberton von c‘ und der 1. Oberton von g‘ fallen in g“ zusammen und bilden einen Peak, der deshalb größer ist als dort erwartet! (Der 1. Oberton wurde jeweils mit der halben und der 2. mit der viertel Amplitude angeregt.)
Nun also ein Spiel mit den Phasen, was, wie schon gesagt, auch wegen der dreidimensionalen Schwingung (also gemischt in einer zusätzlichen Ebene – sowohl parallel als auch senkrecht – zum Gitarren-Griffbrett) tatsächlich nur ein mathematisches „Spielen“ ist, weil das Ohr es nicht unterscheiden kann:
Die Mischung ist tatsächlich symmetrischer, aber das Ohr hört nicht, in welche Richtung die Peaks zeigen, denn die Leistung des Schalls ist mit dem Quadrat der Intensität verbunden, und die ist immer „positiv“…
Nun also wieder der „wohltemperierte“ Fall:
Da haben wir wieder die Schwebung mit gleicher Frequenz (in 2 s etwa 4 mal laut) und die Doppelpeaks bleiben.
3. Diese Spiel können wir nun mit allen Intervallen weiter treiben (was ich auch gemacht habe), aber interessant vwäre doch noch ein Vierklang, wie etwa ein Septakkord c‘-e‘-g‘- b‘ (als Dominant-Septakkord zu F-Dur), oder auch der Vergleich von Dur-Dreiklang und Moll-Dreiklang, oder?
Also hier der Septakkord (nun aber ohne Obertöne, sonst wird es gruselig eng in den Diagrammen):
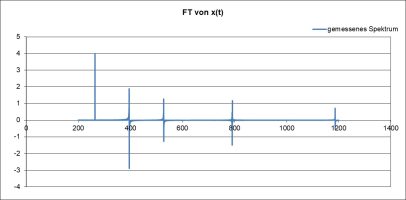
Die Septime ist oben grün eingezeichnet, alle haben die gleiche Amplitude. Im Spektrum haben wir einen Stapel von einer großen Terz und zwei kleinen. Das ist nicht gut zu erkennen, da Intervalle ja Verhältnisse sind und hier aber Frequenz-Differenzen abgebildet sind, weil es eine lineare Abszisse ist. Logarithmieren wir die Abszisse, können die Intervall-Stapel besser erkannt werden. Versuchen wir es:

Logarithmisches Spektrum von 100 bis 1000 Hz, große und kleine Terzen gut unterscheidbar!
Nun also Dur- und Moll-Dreiklang auf c‘, mit Obertönen, die je halbmal schwächer sind.

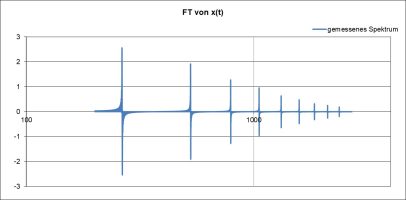
logarithmisches Spektrum mit je 2 Obertönen, große Terz, kleine Terz und Quarte gut gestapelt: c‘-e‘-g‘-c“-e“-g“-h“-d“‚
Schön, zur Schwebung der Quinte sind noch die der Terzen hinzugekommen. Im Spektrum (wieder logarithmisch, jetzt bis auf 2000 Hz erweitert) sind nur 8 Peaks zu sehen, weil zwei von Prime und Quinte zusammenfallen. Hätten wir auch noch den dritten und vierten Oberton dazugenommen, so wäre weiteres Zusammenfallen dazugekommen, denn z.B. der vierte Oberton der Prime fällt mit dem dritten der großen Terz zusammen. (Streng genommen gilt das nur für die reinen Intervalle. Hier haben wir aber wohltemperierte, weshalb auch die Schwebungen da sind…) Schön zu sehen ist auch, dass der Dominant-Dreiklang g-h-d ganz oben dazugekommen ist…
Nun haben wir eine Moll-Dominante dazubekommen…
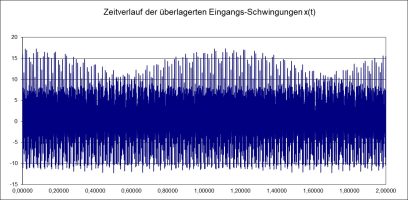
Zum Abschluss dieser Betrachtung noch ein spezielles Spiel mit den physikalischen Obertönen solcher Schwinger wie Saite transversal und Luftsäule longitudinal oder Stab longitudinal, bei welchen die Frequenzen der Obertöne einfach die ganzzahligen Vielfachen der Grundfrequenz sind: Wir betrachten die ersten 8 Obertöne, die also bis zur Sekunde der 3. Oktave gehen, z.B.:
c – c‘ – g‘ – c“ – e“ – g“ – ?“ – c“‚ – d“‚
Das Fragezeichen steht für einen Ton, der zwischen den Halbtönen der diatonischen Tonleiter liegt, so etwa zwischen a“ und b“, aber in anderen Kulturen (persisch z.B.) vorkommt.
Die Überlagerung der Oberschwingungen kann mit den Amplituden und den Phasen variiert werden, was am Spektrum nichts ändert, wohl aber an der Form der Schwingung. Ihre physikalischen Ursachen, physikalischen Wirkungen und ihre Auswirkungen auf das Hören mit dem Ohr könnte man analysieren, wenn man mehr Technik (Lautsprecher zum Umsetzen der erzeugten Schwingungsformen) und mehr physikalische Grundsatzüberlegungen (Energieverteilung, Phasenbeziehungen) einbezieht.
Hier einige ausgewählte Grund-Einstellungen:
a) abnehmende Amplitude, gleiche Phase Cosinus
b) abnehmende Amplitude, gleiche Phase Sinus
c) abnehmende Amplitude, wechselnde Phase Cosinus-Sinus
Die Spektren sind, wie man leicht erkennt, mit Cosinus-Funktionen erzeugt worden.
(Wegen eines fehlenden Lautsprechers an meiner alten Technik kann ich also über die Klangfarbe wenig aussagen… Vielleicht mailt mir jemand seine Eregbnisse in den Kommentaren??)
Dieses Spiel kann man beliebig verfeinern. Viel Spaß beim Weiterdenken!















































Kommentar abgeben